Επιλεγμένες
Ασκήσεις Φυσικής
1)
 Από
ένα σταθερό σημείο κρέμεται ένα ιδανικό ελατήριο σταθεράς k=100Ν/m και με
φυσικό μήκος l0=1m. Στο ελεύθερο άκρο του δένουμε ένα σώμα Σ μάζας
m=2kg και το αφήνουμε ελεύθερο για t=0 από τη θέση φυσικού μήκους του
ελατηρίου.
Από
ένα σταθερό σημείο κρέμεται ένα ιδανικό ελατήριο σταθεράς k=100Ν/m και με
φυσικό μήκος l0=1m. Στο ελεύθερο άκρο του δένουμε ένα σώμα Σ μάζας
m=2kg και το αφήνουμε ελεύθερο για t=0 από τη θέση φυσικού μήκους του
ελατηρίου.
α) Να αποδείξτε ότι το σώμα θα εκτελέσει απλή αρμονική ταλάντωση και να γράψετε την εξίσωση της απομάκρυνσης σε συνάρτηση με το χρόνο θεωρώντας θετική τη φορά προς τα πάνω.
β) Πόσο είναι το μέγιστο μήκος του ελατηρίου και ποιες χρονικές στιγμές το ελατήριο έχει μέγιστο μήκος;
γ) Σε μια στιγμή που το ελατήριο έχει το μέγιστο μήκος του, το σώμα Σ χωρίζεται σε δύο κομμάτια με ίσες μάζες, όπου το ένα συνεχίζει να παραμένει δεμένο με το ελατήριο και ταλαντώνεται στην ίδια διεύθυνση, ενώ το άλλο πέφτει ελεύθερα χωρίς αρχική ταχύτητα. Να υπολογίσετε το νέο πλάτος ταλάντωσης και την αντίστοιχη ενέργεια ταλάντωσης. g=10m/s2
2) Στο
διάγραμμα δίνεται  η
φάση ενός ημιτονοειδούς κύματος πλάτους 0,05m σε συνάρτηση με την
απόσταση από την πηγή τη χρονική στιγμή 6s. Η πηγή βρίσκεται στη θέση
x=0 και για t=0 περνά από τη θέση ισορροπίας της.
η
φάση ενός ημιτονοειδούς κύματος πλάτους 0,05m σε συνάρτηση με την
απόσταση από την πηγή τη χρονική στιγμή 6s. Η πηγή βρίσκεται στη θέση
x=0 και για t=0 περνά από τη θέση ισορροπίας της.
α)Υπολογίστε την ταχύτητα, το μήκος κύματος και την περίοδο του κύματος.
β) Ποια η αρχική φάση της πηγής;
γ) Βρείτε την εξίσωση του κύματος.
δ) Να σχεδιάστε στιγμιότυπο του κύματος την παραπάνω χρονική στιγμή.
3)
Μια σφαίρα μάζας 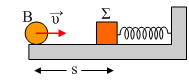 m=1kg
εκτοξεύεται για t=0 με ταχύτητα υ1 από το σημείο Β, το οποίο απέχει
απόσταση s=3m από ακίνητο σώμα Σ, το οποίο ηρεμεί δεμένο στο άκρο οριζόντιου ελατηρίου
σταθεράς k=20Ν/m. Μετά από λίγο η σφαίρα συγκρούεται μετωπικά με το σώμα Σ, το
οποίο μετά την κρούση εκτελεί α.α.τ. με εξίσωση x=(2/π) ημ(πt-π) (μονάδες
S.Ι.). Αν το επίπεδο είναι λείο και η
διάρκεια της κρούσεως αμελητέα, ενώ π2»10, ζητούνται:
m=1kg
εκτοξεύεται για t=0 με ταχύτητα υ1 από το σημείο Β, το οποίο απέχει
απόσταση s=3m από ακίνητο σώμα Σ, το οποίο ηρεμεί δεμένο στο άκρο οριζόντιου ελατηρίου
σταθεράς k=20Ν/m. Μετά από λίγο η σφαίρα συγκρούεται μετωπικά με το σώμα Σ, το
οποίο μετά την κρούση εκτελεί α.α.τ. με εξίσωση x=(2/π) ημ(πt-π) (μονάδες
S.Ι.). Αν το επίπεδο είναι λείο και η
διάρκεια της κρούσεως αμελητέα, ενώ π2»10, ζητούνται:
a) Η ταχύτητα υ1 της σφαίρας.
β) Ποια χρονική στιγμή η σφαίρα θα ξαναπεράσει από το σημείο Β.
γ) Πόσο θα απέχουν μεταξύ τους τη στιγμή αυτή τα δύο σώματα;
4)
Στο άκρο ενός οριζόντιου ελατ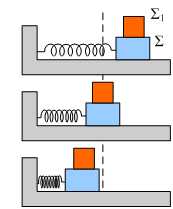 ηρίου
δένουμε ένα σώμα Σ, πάνω του τοποθετούμε ένα δεύτερο σώμα Σ1 μάζας
2kg και το σύστημα τίθεται σε απλή αρμονική ταλάντωση σε λείο οριζόντιο
επίπεδο, με πλάτος Α και περίοδο 2s. Στο διπλανό σχήμα δίνονται τρεις θέσεις.
Στην πρώτη το σύστημα βρίσκεται σε απομάκρυνση x1=0,3m, η δεύτερη
είναι η θέση ισορροπίας, ενώ στην τρίτη η απομάκρυνση x2= - 0,1m.
Και στις τρεις θέσεις το σώμα κινείται προς τ’ αριστερά.
ηρίου
δένουμε ένα σώμα Σ, πάνω του τοποθετούμε ένα δεύτερο σώμα Σ1 μάζας
2kg και το σύστημα τίθεται σε απλή αρμονική ταλάντωση σε λείο οριζόντιο
επίπεδο, με πλάτος Α και περίοδο 2s. Στο διπλανό σχήμα δίνονται τρεις θέσεις.
Στην πρώτη το σύστημα βρίσκεται σε απομάκρυνση x1=0,3m, η δεύτερη
είναι η θέση ισορροπίας, ενώ στην τρίτη η απομάκρυνση x2= - 0,1m.
Και στις τρεις θέσεις το σώμα κινείται προς τ’ αριστερά.
α) Σχεδιάστε τις δυνάμεις που ασκούνται στο σώμα Σ1 στις θέσεις αυτές.
β) Σε ποια θέση η ασκούμενη τριβή είναι μεγαλύτερη;
γ) Υπολογίστε το μέτρο της
τριβής σε όλες τις θέσεις.
Δίνεται ο συντελεστής στατικής οριακής τριβής μεταξύ των δύο σωμάτων μs=0,5.
5)
Δύο σώματα Α και Γ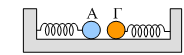 με ίσες μάζες m1=m2=2kg ηρεμούν σε λείο οριζόντιο
επίπεδο, δεμένα στα άκρα δύο ομοίων ελατηρίων σταθεράς k=200Ν/m απέχοντας
μεταξύ τους κατά d=5cm. Συμπιέζουμε το πρώτο ελατήριο, με την βοήθεια του
Α κατά xο=2d και στη συνέχεια
το αφήνουμε να κινηθεί.
με ίσες μάζες m1=m2=2kg ηρεμούν σε λείο οριζόντιο
επίπεδο, δεμένα στα άκρα δύο ομοίων ελατηρίων σταθεράς k=200Ν/m απέχοντας
μεταξύ τους κατά d=5cm. Συμπιέζουμε το πρώτο ελατήριο, με την βοήθεια του
Α κατά xο=2d και στη συνέχεια
το αφήνουμε να κινηθεί.
Να βρεθούν:
α) Τα πλάτη των ταλαντώσεων που θα εκτελέσουν τα δύο σώματα, μετά την μετωπική και ελαστική μεταξύ τους κρούση.
β) Οι εξισώσεις των απομακρύνσεων των δύο σωμάτων σε συνάρτηση με το χρόνο, θεωρώντας t=0 τη στιγμή της κρούσης και x=0 τη θέση ηρεμίας του σώματος Γ.
γ) Αν μετά από χρόνο t = 2Τ/3 (όπου Τ η περίοδος ταλάντωσης), από την στιγμή που άρχισαν οι δύο ταλαντώσεις, τα σώματα συγκρουστούν ξανά, σε πόση απόσταση από την αρχική θέση του Γ θα γίνει η σύγκρουση;
6)
Δύο ταλαντώσεις της ίδιας διεύθυνσης και
γύρω από την ίδια θέση ισορροπίας, έχουν απομακρύνσεις:
y1=2ημ500t (cm) και y2=2ημ(520t
+ π/3).
α) Υπολογίστε το πλάτος της συνισταμένης κίνησης και την απομάκρυνση της κίνησης για t=0 με τη βοήθεια των περιστρεφόμενων διανυσμάτων. Με ποιο άλλο τρόπο θα μπορούσατε να υπολογίσετε τα παραπάνω;
β) Ποια είναι η μέγιστη τιμή του πλάτους; Να σχεδιάστε τα περιστρεφόμενα διανύσματα την στιγμή αυτή καθώς και τη στιγμή που το πλάτος γίνεται μηδέν.
γ) Πόσα μέγιστα του πλάτους έχουμε σε 1sec και πόσα μέγιστα της απομάκρυνσης;
7) Στη θέση x=3m ενός γραμμικού ομογενούς ελαστικού μέσου υπάρχει πηγή κύματος η οποία αρχίζει να ταλαντώνεται σύμφωνα με την εξίσωση y= 0,1ημπt (μονάδες στο S.Ι.) Το κύμα που δημιουργείται διαδίδεται προς τα αριστερά με ταχύτητα υ=1m/s.
α) Να βρείτε την εξίσωση του κύματος που δημιουργείται.
β) Να σχεδιάστε τη μορφή του ελαστικού μέσου τη χρονική στιγμή t1=2,5s.
8) Στο άκρο Ο ενός γραμμικού ελαστικού μέσου υπάρχει πηγή εγκάρσιου κύματος με εξίσωση y=0,01 ημ4π(t-5x) (S.Ι.)
Α) Βρείτε την συχνότητα το μήκος κύματος και την ταχύτητα του κύματος.
Β) Δύο σημεία Κ και Λ απέχουν μεταξύ τους Δx=0,7m και το πλησιέστερο προς την πηγή σημείο Κ έχει εκτελέσει κάποια χρονική στιγμή t1 18 πλήρης ταλαντώσεις. Να βρεθούν:
α) Η διαφορά φάσεως μεταξύ Κ και Λ.
β) Ο αριθμός των ταλαντώσεων που έχει εκτελέσει το σημείο Λ μέχρι τη στιγμή t1.
γ) Ο χρόνος που απαιτείται για να φτάσει το κύμα από το Κ στο Λ.
δ) Αν κάποια χρονική στιγμή το σημείο Κ έχει απομάκρυνση y=0,005m ενώ κινείται προς την θετική κατεύθυνση, ποια η αντίστοιχη απομάκρυνση του σημείου Λ;
Γ) Για τη χρονική στιγμή t2 =20s να υπολογιστούν:
α) Η απόσταση που έχει διαδοθεί το κύμα.
β) Το πλήθος των σημείων του ελαστικού μέσου που διέρχονται από τη θέση ισορροπίας τους.
Δ)Να σχεδιάσετε το στιγμιότυπο του κύματος τη χρονική στιγμή t3= 1,75s.
9)
Κατά μήκος ενός γραμμικού 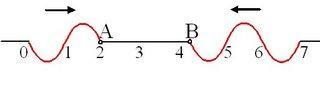 ελαστικού
μέσου διαδίδονται με ταχύτητα υ=1m/s δύο κύματα ίδιου πλάτους και ίδιου μήκους
κύματος και στο σχήμα φαίνεται η μορφή του μέσου τη χρονική στιγμή t0.
ελαστικού
μέσου διαδίδονται με ταχύτητα υ=1m/s δύο κύματα ίδιου πλάτους και ίδιου μήκους
κύματος και στο σχήμα φαίνεται η μορφή του μέσου τη χρονική στιγμή t0.
α) Πόση είναι η φάση του σημείου Α και πόση του σημείου Β τη στιγμή αυτή;
β) Να σχεδιάστε τη μορφή του μέσου τις χρονικές στιγμές:
α) t1=t0+1,5s , β) t2= t0+3s, γ) t3= t0+4s
10) Στα σημεία Α και Β της επιφάνειας ενός υγρού υπάρχουν δύο πηγές οι οποίες για t=0 αρχίζουν να ταλαντώνονται με εξισώσεις:
yΑ=3ημπt (cm) και yΒ = - 3ημπt (cm),
οπότε δημιουργούνται κύματα τα οποία διαδίδονται με ταχύτητα υ=2m/s.
α) Ποιες οι εξισώσεις των κυμάτων που δημιουργούνται;
β) Ένα σημείο Κ απέχει αποστάσεις r1 και r2 από τις πηγές. Ποια η εξίσωση της απομάκρυνσης του σημείου Κ μετά τη συμβολή των δύο κυμάτων;
γ) Ποια σχέση πρέπει να ικανοποιούν οι αποστάσεις r1 και r2 αν θέλουμε το σημείο Κ να:
i) Ταλαντώνεται με πλάτος 6cm.
ii) Παραμένει διαρκώς ακίνητο.
iii) Να ταλαντώνεται με πλάτος 3 cm.
11) Στην επιφάνεια ενός υγρού ορίζεται ένα ορθογώνιο τρίγωνο ΑΒΓ (Α=90°) με πλευρές ΑΒ=3m και ΑΓ=4m. Στις κορυφές Α και Β υπάρχουν δύο πηγές οι οποίες για t=0 αρχίζουν να ταλαντώνονται με εξισώσεις:
yΑ=3ημπt (cm) και yΒ=4ημπt (cm),
οπότε δημιουργούνται κύματα τα οποία διαδίδονται με ταχύτητα υ=2m/s.
A) Να βρεθεί η εξίσωση της απομάκρυνσης σε συνάρτηση με το χρόνο, της κορυφής Γ.
B) Να
βρεθεί η ταχύτητα ταλάντωσης του σημείου Γ τις χρονικές στιγμές:
α) t1=1s, β) t2= 2s γ) t3=3,25s.
12) Κατά μήκος ενός γραμμικού ελαστικού μέσου και από αριστερά προς τα δεξιά διαδίδονται δύο αρμονικά κύματα με το ίδιο πλάτος Α=0,2m και την ίδια συχνότητα f=2Ηz. Η ταχύτητα διάδοσης των κυμάτων είναι ίση με υ=2m/s. Σε ένα σημείο Ο, το οποίο θεωρούμε ως αρχή μέτρησης των αποστάσεων (x=0), το πρώτο κύμα φτάνει κατά τη χρονική στιγμή t=0 και το δεύτερο κύμα κατά τη χρονική στιγμή t1=1s. Θεωρείστε ότι εξαιτίας κάθε κύματος το σημείο Ο αρχίζει να κινείται προς την θετική φορά.
α) Να γραφεί η εξίσωση του κύματος που προκύπτει από τη συμβολή των δύο κυμάτων.
β) Να σχεδιάστε στιγμιότυπο του κύματος τη χρονική στιγμή t2=1,5s
γ) Ποιο το αντίστοιχο διάγραμμα αν το δεύτερο κύμα έφτανε στο σημείο Ο τη χρονική στιγμή t1΄=0,25s;
13) Στις κορυφές Β και Γ ισοπλεύρου τριγώνου πλευράς α=0,5m βρίσκονται δύο πηγές κυμάτων, οι οποίες ταλαντώνονται σύμφωνα με τις εξισώσεις
yΒ=0,1ημ200πt και yΓ=0,1ημ202πt (μονάδες S.Ι.).
Τα κύματα που δημιουργούνται θεωρείται ότι έχουν περίπου το ίδιο μήκος κύματος λ=2m.
α) Να βρείτε την εξίσωση της κίνησης της κορυφής Α.
β) Να κάνετε το γράφημα yΑ = f(t) θεωρώντας χρονική στιγμή t=0 τη στιγμή που τα δύο κύματα φτάνουν ταυτόχρονα στην κορυφή Α και για το χρονικό διάστημα από 0-2s.
γ) Πόσες ταλαντώσεις εκτελεί η κορυφή Α στο παραπάνω χρονικό διάστημα;
14) Μια ακτίνα μονοχρωματικού φωτός προσπίπτει σε μια σφαιρική σταγόνα νερού (όπως στο ουράνιο τόξο), υπό γωνία φ.
 α)
Να αποδείξτε ότι για οποιαδήποτε γωνία πρόσπτωσης φ, δεν θα υπάρξει ολική
ανάκλαση στο σημείο Α.
α)
Να αποδείξτε ότι για οποιαδήποτε γωνία πρόσπτωσης φ, δεν θα υπάρξει ολική
ανάκλαση στο σημείο Α.
β) Πώς προκύπτει η τελική ακτίνα, που εξέρχεται από το σημείο Β;
γ) Ποια η γωνία που σχηματίζει η εξερχόμενη ακτίνα στο σημείο Β με την ακτίνα της σφαίρας;
15) Ο τροχός ενός αυτοκινήτου έχει ακτίνα R=0,8m. Τα αυτοκίνητο για t=0 ξεκινά από την ηρεμία με επιτάχυνση 2m/s2 ενώ ο τροχός αποκτά σταθερή γωνιακή επιτάχυνση αγων=2rad/s2. Για τη χρονική στιγμή t=5s, να υπολογιστούν:
a) Η ταχύτητα του αυτοκινήτου και η μετατόπιση του κέντρου Ο του τροχού του.
β) Η γωνιακή ταχύτητα περιστροφής του τροχού.
γ) Η ταχύτητα και η επιτάχυνση του σημείου επαφής Α του τροχού με το έδαφος.
δ) Ο τροχός του αυτοκινήτου:
ι) Κυλίεται χωρίς ολίσθηση, ii) Ολισθαίνει ii) Σπινάρει.
Επιλέξτε την σωστή απάντηση δικαιολογώντας την άποψή σας.
16) Πάνω
σε ένα λείο οριζόντιο επίπεδο ηρεμεί μια 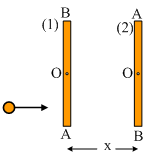 σανίδα μήκους ;=4m (θέση 1). Μια σφαίρα που
κινείται οριζόντια κτυπά τη ράβδο, με αποτέλεσμα αμέσως μετά την κρούση τα άκρα
Α και Β της ράβδου να έχουν ταχύτητες με κατεύθυνση προς τα δεξιά και μέτρα υΑ=6m/s
και υΒ=2m/s αντίστοιχα.
σανίδα μήκους ;=4m (θέση 1). Μια σφαίρα που
κινείται οριζόντια κτυπά τη ράβδο, με αποτέλεσμα αμέσως μετά την κρούση τα άκρα
Α και Β της ράβδου να έχουν ταχύτητες με κατεύθυνση προς τα δεξιά και μέτρα υΑ=6m/s
και υΒ=2m/s αντίστοιχα.
α) Ποια η ταχύτητα του μέσου Ο της σανίδας;
β) Βρείτε την γωνιακή ταχύτητα περιστροφής της σανίδας.
γ) Ποια η προς τα δεξιά
μετατόπιση x του άκρου Α, τη στιγμή που η σανίδα βρίσκεται στη θέση (2) για
πρώτη φορά;
Δίνεται ότι η κίνηση είναι ομαλή μετά την κρούση.
17) Μια
ράβδος μήκους : = 20/π m στρέ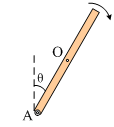 φεται
σε κατακόρυφο επίπεδο γύρω από σταθερό οριζόντιο άξονα που διέρχεται από το
άκρο της Α. Σε μια στιγμή που η ράβδος σχηματίζει με την κατακόρυφο γωνία θ=30°
έχοντας γωνιακή ταχύτητα ω=π rad/s ο άξονας σπάει και η ράβδος
κινείται ελεύθερα. Μετά από χρόνο t=2s:
φεται
σε κατακόρυφο επίπεδο γύρω από σταθερό οριζόντιο άξονα που διέρχεται από το
άκρο της Α. Σε μια στιγμή που η ράβδος σχηματίζει με την κατακόρυφο γωνία θ=30°
έχοντας γωνιακή ταχύτητα ω=π rad/s ο άξονας σπάει και η ράβδος
κινείται ελεύθερα. Μετά από χρόνο t=2s:
α) Πόσο έχει πέσει κατακόρυφα το μέσον Ο της ράβδου;
β) Ποια η οριζόντια μετατόπιση του μέσου της ράβδου Ο;
γ) Σχεδιάστε στο σχήμα τη θέση της ράβδου. g=10m/s2
18) Ένας
άνθρωπος αρπάζει  μια
ομογενή ράβδο μήκους 40cm
από ένα τυχαίο σημείο της και την πετάει στον αέρα, με τέτοιο τρόπο ώστε το άκρο
της ράβδου που είναι πλησιέστερα προς αυτόν να έχει ταχύτητα μηδέν τη στιγμή
που η ράβδος φεύγει από τα χέρια του. Αν η ράβδος συμπληρώσει δύο περιστροφές
πριν την ξαναπιάσει ο άνθρωπος στο ίδιο ύψος απ’ όπου την άφησε, να αποδείξτε
ότι το ύψος που φτάνει το κέντρο μάζας της ράβδου είναι ίσο με h=0,4·π (m)
μια
ομογενή ράβδο μήκους 40cm
από ένα τυχαίο σημείο της και την πετάει στον αέρα, με τέτοιο τρόπο ώστε το άκρο
της ράβδου που είναι πλησιέστερα προς αυτόν να έχει ταχύτητα μηδέν τη στιγμή
που η ράβδος φεύγει από τα χέρια του. Αν η ράβδος συμπληρώσει δύο περιστροφές
πριν την ξαναπιάσει ο άνθρωπος στο ίδιο ύψος απ’ όπου την άφησε, να αποδείξτε
ότι το ύψος που φτάνει το κέντρο μάζας της ράβδου είναι ίσο με h=0,4·π (m)
19) Σε
οριζόντιο επίπεδο ηρεμεί ένας 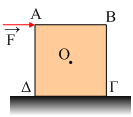 κύβος
ακμής α=1m και μάζας m=30kg, ο οποίος εμφανίζει με το επίπεδο συντελεστές
τριβής μ=μs=0,6. Σε μια στιγμή δέχεται την επίδραση μιας οριζόντιας
δύναμης μέτρου F=60Ν στην κορυφή Α, όπως στο σχήμα.
κύβος
ακμής α=1m και μάζας m=30kg, ο οποίος εμφανίζει με το επίπεδο συντελεστές
τριβής μ=μs=0,6. Σε μια στιγμή δέχεται την επίδραση μιας οριζόντιας
δύναμης μέτρου F=60Ν στην κορυφή Α, όπως στο σχήμα.
α) Υπολογίστε τις δυνάμεις που ασκούνται στο κύβο, καθώς και τη ροπή καθεμιάς ως προς το κέντρο Ο του κύβου,
β) Αν αυξήσουμε το μέτρο της δύναμης F ποια η μέγιστη τιμή που μπορεί να πάρει, χωρίς να ανατραπεί ο κύβος; g=10m/s2.
20)
Ένας τροχός μάζας 40kg και ακτίνας
 R=0,5m
στρέφεται με γωνιακή ταχύτητα ω0=60rad/s. Σε μια στιγμή ο τροχός αφήνεται σε οριζόντιο επίπεδο με το
οποίο παρουσιάζει συντελεστή τριβής ολίσθησης μ=0,2. Αν ροπή αδράνειας του
τροχού ως προ τον άξονα περιστροφής του δίνεται από τη σχέση Ι= ½ m·R2 και g=10m/s2
ζητούνται:
R=0,5m
στρέφεται με γωνιακή ταχύτητα ω0=60rad/s. Σε μια στιγμή ο τροχός αφήνεται σε οριζόντιο επίπεδο με το
οποίο παρουσιάζει συντελεστή τριβής ολίσθησης μ=0,2. Αν ροπή αδράνειας του
τροχού ως προ τον άξονα περιστροφής του δίνεται από τη σχέση Ι= ½ m·R2 και g=10m/s2
ζητούνται:
α) Η γωνιακή επιτάχυνση (επιβράδυνση) που θα αποκτήσει.
β) Η επιτάχυνση του άξονα του τροχού.
γ) Μετά από πόσο χρόνο ο τροχός θα κυλίεται χωρίς να ολισθαίνει και πόσο θα έχει στο μεταξύ μετατοπισθεί ο άξονάς του;
δ) Πόσες περιστροφές έκανε ο τροχός μέχρι να πάψει την ολίσθησή του;
21) 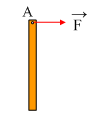 Σε
λείο οριζόντιο επίπεδο ηρεμεί μια ομογενής σανίδα μάζας 2kg. Σε μια στιγμή στο
άκρον της Α ασκείται δύναμη F=2Ν, όπως στο σχήμα. Να βρείτε την επιτάχυνση που
αποκτά το σημείο Α για t=0+.
Σε
λείο οριζόντιο επίπεδο ηρεμεί μια ομογενής σανίδα μάζας 2kg. Σε μια στιγμή στο
άκρον της Α ασκείται δύναμη F=2Ν, όπως στο σχήμα. Να βρείτε την επιτάχυνση που
αποκτά το σημείο Α για t=0+.
Η ροπή αδράνειας της σανίδας ως προς άξονα που είναι κάθετος σε αυτήν και
περνάει από το μέσον της Ιcm = 1/12 ml2.
22)
Μια ομογενής σανίδα μήκους l =6m και μάζας m=2kg
αφήνεται για t=0 από οριζόντια θέση να κινηθεί, ενώ μέσω νήματος ασκείται πάνω
της κατακόρυφη δύναμη F=10Ν, όπως στο σχήμα. Να βρεθούν για τη χρονική στιγμή
t=0+:
l =6m και μάζας m=2kg
αφήνεται για t=0 από οριζόντια θέση να κινηθεί, ενώ μέσω νήματος ασκείται πάνω
της κατακόρυφη δύναμη F=10Ν, όπως στο σχήμα. Να βρεθούν για τη χρονική στιγμή
t=0+:
α) Η επιτάχυνση του κέντρου μάζας της σανίδας.
β) Η γωνιακή της επιτάχυνση.
γ) Η επιτάχυνση του σημείου Α.
Δίνονται g=10m/s2 και για τη ροπή αδράνειας της ράβδου ως προς άξονα που διέρχεται από το μέσον της Ιcm = 1/12ml 2.
23)
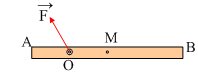 Μια
ομογενής ράβδος μήκους l
=2m και μάζας m=10kg μπορεί να στρέφεται γύρω από οριζόντιο άξονα, ο οποίος
διέρχεται από το σημείο Ο, όπου (ΑΟ)=0,5m. Αφήνουμε την ράβδο από μια ορισμένη
θέση, οπότε τη στιγμή που γίνεται οριζόντια, όπως στο σχήμα, έχει γωνιακή ταχύτητα
ω=3rad/s. Για την θέση αυτή
ζητούνται:
Μια
ομογενής ράβδος μήκους l
=2m και μάζας m=10kg μπορεί να στρέφεται γύρω από οριζόντιο άξονα, ο οποίος
διέρχεται από το σημείο Ο, όπου (ΑΟ)=0,5m. Αφήνουμε την ράβδο από μια ορισμένη
θέση, οπότε τη στιγμή που γίνεται οριζόντια, όπως στο σχήμα, έχει γωνιακή ταχύτητα
ω=3rad/s. Για την θέση αυτή
ζητούνται:
α) Η ταχύτητα του μέσου Μ της ράβδου.
β) Η γωνιακή επιτάχυνση της ράβδου.
γ) Ο ρυθμός μεταβολής του μέτρου της ταχύτητας του μέσου Μ της ράβδου.
δ) Η οριζόντια και η κατακόρυφη συνιστώσα της δύναμης >F που δέχεται η ράβδος από τον άξονα περιστροφής.
Δίνονται η ροπή αδράνειας της ράβδου ως προς κάθετο άξονα που διέρχεται από το μέσον της Ι= 1/12 ml 2 και g=10m/s2.
24)
Η ομογενής ράβδος του σχήματος, έχει μήκος 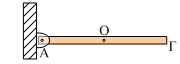 l =3m, είναι αρθρωμένη σε κατακόρυφο τοίχο και συγκρατείται σε
οριζόντια θέση. Σε μια στιγμή t=0 αφήνεται ελεύθερη να κινηθεί. Αμέσως μετά
(t=0+):
l =3m, είναι αρθρωμένη σε κατακόρυφο τοίχο και συγκρατείται σε
οριζόντια θέση. Σε μια στιγμή t=0 αφήνεται ελεύθερη να κινηθεί. Αμέσως μετά
(t=0+):
α) Βρείτε την επιτάχυνση του άκρου Γ και του μέσου Ο της ράβδου.
β)Να κάνετε τη γραφική παράσταση της επιτάχυνσης των διαφόρων σημείων της ράβδου, σε συνάρτηση με την απόστασή τους από το άκρο Α.
α) Αν στο άκρο Γ είχαμε τοποθετήσει ένα μικρό νόμισμα, τι κίνηση θα πραγματοποιούσε όταν αφήναμε τη ράβδο να κινηθεί;
β) Ποια η μέγιστη απόσταση από τον άξονα περιστροφής, στην οποία θα πρέπει να τοποθετηθεί το νόμισμα για να ξεκινήσει την κίνησή του μαζί με τη ράβδο;
Δίνεται η ροπή αδράνειας μιας ράβδου ως προς κάθετο άξονα ο οποίος διέρχεται από το μέσον της Ι= 1/12ml2 και g=10m/s2.
25)
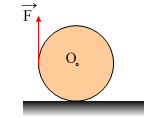 Ένας
ομογενής κύλινδρος μάζας 4kg ηρεμεί σε οριζόντιο επίπεδο με το οποίο
παρουσιάζει συντελεστές τριβής μs=μ= 1/3 . Τυλίγουμε γύρω του ένα αβαρές νήμα μέσω του
οποίου ασκούμε στον κύλινδρο μια σταθερή κατακόρυφη δύναμη F=3Ν όπως στο
σχήμα.
Ένας
ομογενής κύλινδρος μάζας 4kg ηρεμεί σε οριζόντιο επίπεδο με το οποίο
παρουσιάζει συντελεστές τριβής μs=μ= 1/3 . Τυλίγουμε γύρω του ένα αβαρές νήμα μέσω του
οποίου ασκούμε στον κύλινδρο μια σταθερή κατακόρυφη δύναμη F=3Ν όπως στο
σχήμα.
α) Αποδείξτε ότι ο κύλινδρος θα κινηθεί οριζόντια.
β) Θεωρώντας ότι ο κύλινδρος κυλίεται χωρίς να ολισθαίνει, βρείτε την επιτάχυνση του άξονά του.
γ) Αν αυξάνουμε σιγά – σιγά το μέτρο της δύναμης F, ποια είναι η μέγιστη τιμή που μπορεί να πάρει χωρίς να ολισθήσει ο κύλινδρος; Ποια είναι τότε η μέγιστη τιμή της επιτάχυνσης του κυλίνδρου;
Δίνεται η ροπή αδράνειας του κυλίνδρου Ι= ½ mR2 και g=10m/s2.
26) Σε λείο οριζόντιο επίπεδο ηρεμούν τρία σώματα της ίδιας μάζας Μ. Το πρώτο είναι ένας κύβος ενώ τα δύο άλλα δύο όμοιοι κύλινδροι της ίδιας ακτίνας R. Σε μια στιγμή t=0, ασκούνται πάνω τους τρεις ίσες σταθερές δυνάμεις F1=F2=F3, όπως στο σχήμα, όπου οι δύο πρώτες δυνάμεις ασκούνται στα κέντρα των σωμάτων, ενώ η τρίτη ασκείται πάντα στην περιφέρεια του κυλίνδρου.
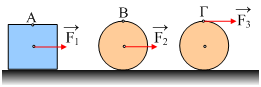
α) Να συγκρίνετε τις επιταχύνσεις του κέντρου μάζας των τριών σωμάτων.
β) Να συγκρίνετε τις ταχύτητες των σημείων Α, Β και Γ μετά από χρονικό διάστημα t1.
γ) Για τη χρονική στιγμή t1 να υπολογίστε τους λόγους:
α) ![]() και
και ![]() όπου W τα αντίστοιχα
έργα των δυνάμεων.
όπου W τα αντίστοιχα
έργα των δυνάμεων.
Δίνεται η ροπή αδράνειας του κυλίνδρου ως προς τον άξονά του Ι= ½ mR2.
27)
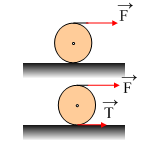 Γύρω
από δύο όμοιους ομογενείς κυλίνδρους τυλίγουμε αβαρή νήματα. Τοποθετούμε τον
πρώτο σε λείο οριζόντιο επίπεδο και τον δεύτερο σε οριζόντιο επίπεδο με τριβές.
Τραβώντας τα νήματα ασκούμε πάνω τους ίσες δυνάμεις για ίσα χρονικά διαστήματα
t1, όπως στο σχήμα. Με δεδομένο ότι ο δεύτερος κύλινδρος κυλίεται χωρίς να ολισθαίνει,
να συγκρίνετε:
Γύρω
από δύο όμοιους ομογενείς κυλίνδρους τυλίγουμε αβαρή νήματα. Τοποθετούμε τον
πρώτο σε λείο οριζόντιο επίπεδο και τον δεύτερο σε οριζόντιο επίπεδο με τριβές.
Τραβώντας τα νήματα ασκούμε πάνω τους ίσες δυνάμεις για ίσα χρονικά διαστήματα
t1, όπως στο σχήμα. Με δεδομένο ότι ο δεύτερος κύλινδρος κυλίεται χωρίς να ολισθαίνει,
να συγκρίνετε:
α) Τις επιταχύνσεις των αξόνων των δύο κυλίνδρων.
β) Τις ταχύτητες που αποκτούν οι δύο κύλινδροι.
γ) Τις γωνιακές ταχύτητες των δύο κυλίνδρων.
δ) Τις οριζόντιες μετατοπίσεις των κέντρων μάζας των κυλίνδρων.
ε) Τις ταχύτητες των σημείων Γ και Δ των σημείων επαφής των δύο κυλίνδρων με το επίπεδο.
Στ) Αν μετά τη χρονική στιγμή t1 παύει η εξάσκηση των δυνάμεων, να περιγράψτε τις κινήσεις των δύο κυλίνδρων, από κει και πέρα.
28)
 Δίνεται
το σύστημα των δύο τροχών του σχήματος, ακτίνας R=1m, οι οποίοι συνδέονται με κύλινδρο ακτίνας
r=0,5m. Η μάζα του συστήματος
είναι ίση με10kg, ενώ η ροπή αδράνειας ως προς τον άξονα του περιστροφής του
κυλίνδρου Ι=3kgKm2. Γύρω
από τον κύλινδρο τυλίγουμε αβαρές νήμα, μέσω του οποίου ασκούμε οριζόντια δύναμη
=F, όπως δείχνεται στο κάτω
σχήμα, ενώ οι τροχοί παρουσιάζουν με το έδαφος συντελεστές τριβής μs=μ=0,5.
Δίνεται
το σύστημα των δύο τροχών του σχήματος, ακτίνας R=1m, οι οποίοι συνδέονται με κύλινδρο ακτίνας
r=0,5m. Η μάζα του συστήματος
είναι ίση με10kg, ενώ η ροπή αδράνειας ως προς τον άξονα του περιστροφής του
κυλίνδρου Ι=3kgKm2. Γύρω
από τον κύλινδρο τυλίγουμε αβαρές νήμα, μέσω του οποίου ασκούμε οριζόντια δύναμη
=F, όπως δείχνεται στο κάτω
σχήμα, ενώ οι τροχοί παρουσιάζουν με το έδαφος συντελεστές τριβής μs=μ=0,5.
α) Αν F=35Ν, να βρείτε την επιτάχυνση και τη γωνιακή επιτάχυνση του συστήματος.
β) Αυξάνουμε σιγά-σιγά το μέτρο της δύναμης F. Ποια είναι η μέγιστη τιμή της δύναμης για την οποία δεν παρατηρείται ολίσθηση;
γ) Αν F=112Ν ποια η επιτάχυνση και ποια η γωνιακή επιτάχυνση του συστήματος; Περιγράψτε την κίνηση του συστήματος στην περίπτωση αυτή.
29)
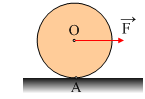 Κυλίεται μόνο ή και ολισθαίνει;
Κυλίεται μόνο ή και ολισθαίνει;
Στο διπλανό σχήμα φαίνεται ένας τροχός, μάζας m=2kg και ακτίνας R=1m που ηρεμεί σ’ οριζόντιο επίπεδο, με το οποίο παρουσιάζει συντελεστές τριβής οριακής μs=0,15 και ολίσθησης μ=0,1. Για t=0 ασκούμε πάνω του οριζόντια δύναμη F=12Ν.
α) Σχεδιάστε τις δυνάμεις που ασκούνται πάνω του και δώστε τις εξισώσεις από τις οποίες υπολογίζουμε την επιτάχυνση του κέντρου μάζας Ο και την γωνιακή επιτάχυνση του τροχού.
β) Για να βρούμε αν η τριβή είναι στατική ή ολίσθησης, υποθέτουμε ότι ο τροχός δεν ολισθαίνει. Ποια σχέση συνδέει τις δύο παραπάνω επιταχύνσεις;
γ) Με βάση την παραπάνω προϋπόθεση, υπολογίστε την τιμή του μέτρου της τριβής. Είναι αποδεκτή η τιμή που υπολογίσατε; Σε τι συμπέρασμα καταλήγετε;
δ) Τι κίνηση τελικά εκτελεί το σώμα και ποια η ταχύτητα του σημείου Α για t=2s;
ε) Ποια η ελάχιστη τιμή του συντελεστή στατικής τριβής, ώστε ο τροχός να κυλίεται μόνο χωρίς να ολισθαίνει;
Δίνονται για τον τροχό Ιcm = ½ m·R2 και g=10m/s2.
30)
Ένας τροχός μάζας m=10kg και ακτίνας R=1m είναι
ακίνητος σε  οριζόντιο
επίπεδο (1), απέχοντας απόσταση d=8m από δεύτερο επίπεδο (2). Για t=0 ασκείται
στο κέντρο του Ο μια οριζόντια δύναμη F=60Ν. Οι συντελεστές τριβής μεταξύ
τροχού και των δύο επιπέδων είναι μs1=μ1=0,5 και μs2=μ2=0,1.
Ποια η ταχύτητα του κέντρου Ο και ποια η γωνιακή ταχύτητα περιστροφής του
τροχού:
οριζόντιο
επίπεδο (1), απέχοντας απόσταση d=8m από δεύτερο επίπεδο (2). Για t=0 ασκείται
στο κέντρο του Ο μια οριζόντια δύναμη F=60Ν. Οι συντελεστές τριβής μεταξύ
τροχού και των δύο επιπέδων είναι μs1=μ1=0,5 και μs2=μ2=0,1.
Ποια η ταχύτητα του κέντρου Ο και ποια η γωνιακή ταχύτητα περιστροφής του
τροχού:
α) Τη στιγμή που περνά από το ένα επίπεδο στο άλλο.
β) Τη χρονική στιγμή t1=4s.
Για τον τροχό Ι= ½ mR2 και g=10m/s2.
31) Και αν είναι τροχός αυτοκινήτου;…….
Ένας τροχός αυτοκινήτου μάζας 10kg, ακτίνας R=0,4m ηρεμεί σε οριζόντιο
επίπεδο με το οποίο παρουσιάζει συντελεστές τριβής μs=0,5 και μ=0,4.
Σε μια στιγμή t=0, δέχεται σταθερή ροπή ως προς τον άξονά του τ= 48ΝKm, μέσω του συστήματος κίνησης, μέχρι τη
χρονική στιγμή t1=2s, οπότε μηδενίζεται. Ας αγνοήσουμε το υπόλοιπο
αυτοκίνητο και ας μελετήσουμε την κίνηση του τροχού σαν μεμονωμένο σώμα, θεωρώντας
ότι ως προς τον άξονά του Ι= ½ m·R2.
α) Σχεδιάστε ένα σχήμα στο οποίο να εμφανίζονται οι δυνάμεις που ασκούνται στον τροχό.
β) Πώς υπολογίζουμε την επιτάχυνση και πώς τη γωνιακή επιτάχυνση του τροχού;
γ) Ας υποθέσουμε ότι ο τροχός κυλίεται και δεν ολισθαίνει. Με την υπόθεση αυτή ποια η επιτάχυνση που αποκτά ο τροχός και ποια τιμή παίρνει η τριβή; Είναι αποδεκτή η παραπάνω τιμή;
δ) Ποια η επιτάχυνση, η ταχύτητα και η γωνιακή ταχύτητα του τροχού για t1 =2s;
ε) Ποια χρονική στιγμή ο τροχός σταματά να ολισθαίνει και κυλίεται μόνο;
στ) Να γίνουν οι γραφικές παραστάσεις της ταχύτητας του κέντρου του τροχού και του μέτρου της γωνιακής του ταχύτητας, σε συνάρτηση με το χρόνο. g=10m/s2.
32)
Σε λείο οριζόντιο επίπεδο γλιστράει με 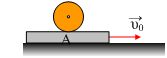 αρχική
ταχύτητα υ0=10m/s μια σανίδα μάζας Μ=10kg. Σε μια στιγμή t=0,
αφήνουμε πάνω της έναν ομογενή κύλινδρο μάζας m1=2kg και ακτίνας
R=0,2m, χωρίς αρχική ταχύτητα αλλά και χωρίς να στρέφεται. Αν ο συντελεστής
τριβής ολίσθησης μεταξύ κυλίνδρου και σανίδας είναι μ=0,1, ενώ για τον κύλινδρο
Ι= ½ m·R2, να
βρείτε:
αρχική
ταχύτητα υ0=10m/s μια σανίδα μάζας Μ=10kg. Σε μια στιγμή t=0,
αφήνουμε πάνω της έναν ομογενή κύλινδρο μάζας m1=2kg και ακτίνας
R=0,2m, χωρίς αρχική ταχύτητα αλλά και χωρίς να στρέφεται. Αν ο συντελεστής
τριβής ολίσθησης μεταξύ κυλίνδρου και σανίδας είναι μ=0,1, ενώ για τον κύλινδρο
Ι= ½ m·R2, να
βρείτε:
α) Την επιβράδυνση της σανίδας.
β) Την επιτάχυνση του άξονα του κυλίνδρου.
γ) Τη γωνιακή επιτάχυνση του κυλίνδρου.
δ) Την ταχύτητα ενός σημείου επαφής του κυλίνδρου με τη σανίδα (σημείο Α) τη χρονική στιγμή t1 =2s.
33)
Μια ομογενής ράβδος μήκους l=4m και μάζας 12kg 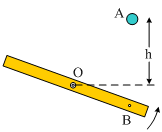 στρέφεται
γύρω από οριζόντιο άξονα ο οποίος περνά από το μέσον της Ο, με σταθερή γωνιακή
ταχύτητα ω=4rad/s αντίθετα
από τους δείκτες του ρολογιού. Από ένα σημείο Α που βρίσκεται σε ύψος h=1,25m
πάνω από το οριζόντιο επίπεδο που περνά από το Ο, αφήνουμε για t=0 μια σφαίρα Σ
μάζας m1=2kg να πέσει ελεύθερα. Η σφαίρα συγκρούεται πλαστικά με τη
ράβδο, τη στιγμή που ήταν σε οριζόντια θέση και σε σημείο Β, όπου (ΟΒ)=1,5m.
Ζητούνται:
στρέφεται
γύρω από οριζόντιο άξονα ο οποίος περνά από το μέσον της Ο, με σταθερή γωνιακή
ταχύτητα ω=4rad/s αντίθετα
από τους δείκτες του ρολογιού. Από ένα σημείο Α που βρίσκεται σε ύψος h=1,25m
πάνω από το οριζόντιο επίπεδο που περνά από το Ο, αφήνουμε για t=0 μια σφαίρα Σ
μάζας m1=2kg να πέσει ελεύθερα. Η σφαίρα συγκρούεται πλαστικά με τη
ράβδο, τη στιγμή που ήταν σε οριζόντια θέση και σε σημείο Β, όπου (ΟΒ)=1,5m.
Ζητούνται:
i) Για τη χρονική στιγμή t=0,2s:
a) Η ολική στροφορμή του συστήματος ως προς τον άξονα περιστροφής της ράβδου.
b) Ο ρυθμός μεταβολής της στροφορμής, ως προς τον
άξονα περιστροφής της ράβδου:
1) της ράβδου
2) της σφαίρας
3) του συστήματος ράβδος – σφαίρα.
ii) Αν η κρούση διαρκεί απειροελάχιστα, για αμέσως μετά την κρούση:
a) Ποια η γωνιακή ταχύτητα περιστροφής του συστήματος;
β) Ποιος ο ρυθμός μεταβολής της στροφορμής, ως προς τον άξονα περιστροφής, του συστήματος;
Δίνεται η ροπή αδράνειας μιας ράβδου ως προς κάθετο σε αυτήν άξονα που περνά από το μέσον της Ι= 1/12Μl 2.
34) Στην επιφάνεια μιας παγωμένης λίμνης ηρεμεί μια ομογενής σανίδα μήκους 4m και μάζας Μ=3kg. Ένα βλήμα μάζας m=0,1kg κινείται οριζόντια με ταχύτητα μέτρου υ0=200m/s και διεύθυνση κάθετη στη σανίδα, κτυπά τη σανίδα σε σημείο Ο, το οποίο απέχει d=1m από το ένα της άκρο, την διαπερνά και εξέρχεται με ταχύτητα υ=50m/s.
a) Βρείτε την ταχύτητα του κέντρου μάζας της σανίδας μετά τη κρούση.
β) Υπολογίστε τη γωνιακή ταχύτητα περιστροφής που θα αποκτήσει η σανίδα.
γ) Ποιο το μέτρο της ταχύτητας του σημείου Ο αμέσως μετά τη σύγκρουση;
Δίνεται η ροπή αδράνειας μιας ράβδου ως προς κάθετο άξονα που διέρχεται από το μέσον της Ι= 1/12ml2.
35)
 Μια
ράβδος μήκους l και
μάζας m ηρεμεί σε λείο οριζόντιο επίπεδο. Μια μπάλα, ίδιας μάζας m, που
θεωρείται υλικό σημείο κινείται στο ίδιο οριζόντιο επίπεδο, κάθετα προς τη
ράβδο, με ταχύτητα υ0=20m/s και προσκολλάται στο άκρο Α της ράβδου.
Να βρεθεί η ταχύτητα του άκρου Α αμέσως μετά την κρούση, όταν:
Μια
ράβδος μήκους l και
μάζας m ηρεμεί σε λείο οριζόντιο επίπεδο. Μια μπάλα, ίδιας μάζας m, που
θεωρείται υλικό σημείο κινείται στο ίδιο οριζόντιο επίπεδο, κάθετα προς τη
ράβδο, με ταχύτητα υ0=20m/s και προσκολλάται στο άκρο Α της ράβδου.
Να βρεθεί η ταχύτητα του άκρου Α αμέσως μετά την κρούση, όταν:
α) Η ράβδος μπορεί να στρέφεται γύρω από κατακόρυφο άξονα ο οποίος περνά από το άκρο Ο της ράβδου.
β) Η ράβδος είναι ελεύθερη να κινηθεί.
Δίνεται η ροπή αδράνειας μιας ράβδου ως προς κάθετο άξονα που διέρχεται από το
μέσον της Ι= 1/12ml
2.
36)
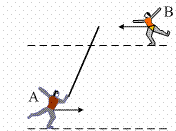 Οι
παγοδρόμοι Α και Β έχουν ίσες μάζες m1
= m2=60kg και
κινούνται ευθύγραμμα κατά μήκος των παραλλήλων γραμμών που απέχουν μεταξύ τους
4 m. Οι παγοδρόμοι έχουν ταχύτητες με μέτρα υΑ=10m/s και υΒ=8m/s
και αντίθετης φοράς ώστε να πλησιάζει ο ένας τον άλλον. Ο παγοδρόμος Α κρατάει
στο χέρι του την μια άκρη ενός κονταριού μήκους 4 m και αμελητέας μάζας. Όταν
οι παγοδρόμοι πλησιάσουν στην μικρότερη απόσταση, ο Β πιάνει την ελεύθερη άκρη
του κονταριού και πιασμένοι από τις άκρες του συνεχίζουν να κινούνται.
Οι
παγοδρόμοι Α και Β έχουν ίσες μάζες m1
= m2=60kg και
κινούνται ευθύγραμμα κατά μήκος των παραλλήλων γραμμών που απέχουν μεταξύ τους
4 m. Οι παγοδρόμοι έχουν ταχύτητες με μέτρα υΑ=10m/s και υΒ=8m/s
και αντίθετης φοράς ώστε να πλησιάζει ο ένας τον άλλον. Ο παγοδρόμος Α κρατάει
στο χέρι του την μια άκρη ενός κονταριού μήκους 4 m και αμελητέας μάζας. Όταν
οι παγοδρόμοι πλησιάσουν στην μικρότερη απόσταση, ο Β πιάνει την ελεύθερη άκρη
του κονταριού και πιασμένοι από τις άκρες του συνεχίζουν να κινούνται.
α) Εξηγείστε και δικαιολογείστε με σαφήνεια ποιο θα είναι το είδος της κίνησης που θα εκτελούν οι παγοδρόμοι, από την στιγμή που συνδέονται και οι δύο στο κοντάρι και μετά.
β) Υπολογίστε την ταχύτητα του κέντρου μάζας του συστήματος των δύο παγοδρόμων καθώς και την γωνιακή ταχύτητα περιστροφής του συστήματος.
37)
Σε λείο οριζόντιο επίπεδο ηρεμεί 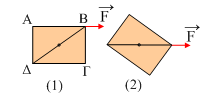 μια
ορθογώνια πλάκα μάζας Μ=12kg και πλευρών α=4m και β=3m. Σε μια στιγμή
δέχεται στην κορυφή Β μια σταθερή
οριζόντια δύναμη μέτρου F=24Ν, οπότε μετά από χρόνο t=1s η πλάκα έχει περιστραφεί
κατά θ, φτάνοντας στη θέση που φαίνεται στο σχήμα 2 .
μια
ορθογώνια πλάκα μάζας Μ=12kg και πλευρών α=4m και β=3m. Σε μια στιγμή
δέχεται στην κορυφή Β μια σταθερή
οριζόντια δύναμη μέτρου F=24Ν, οπότε μετά από χρόνο t=1s η πλάκα έχει περιστραφεί
κατά θ, φτάνοντας στη θέση που φαίνεται στο σχήμα 2 .
i) Να περιγράψετε την κίνηση της πλάκας.
ii) Να χαρακτηρίστε σαν σωστές ή λαθεμένες τις παρακάτω προτάσεις:
α) Η πλάκα εκτελεί ευθύγραμμη ομαλά επιταχυνόμενη κίνηση και ομαλά επιταχυνόμενη στροφική κίνηση.
β) Η πλάκα στρέφεται γύρω από οριζόντιο άξονα που διέρχεται από το κέντρο της.
γ) Η πλάκα στρέφεται γύρω από κατακόρυφο άξονα που διέρχεται από το κέντρο της.
δ) Η γωνιακή ταχύτητα περιστροφής της πλάκας μπορεί να υπολογιστεί από την εξίσωση θ= ½ αt2.
iii) Υπολογίστε την ταχύτητα του κέντρου Ο της πλάκας στη θέση (2).
iv) Βρείτε το έργο της δύναμης F μεταξύ των θέσεων (1) και (2).
v) Πόση είναι η γωνιακή ταχύτητα της πλάκας στη θέση (2);
Δίνεται η ροπή αδράνειας της πλάκας ως προς άξονα κάθετο στην πλάκα που διέρχεται από το κέντρο της Ι= 1/12Μ (α2+ β2).
38)
Τοποθετούμε τη μύτη ενός μολυβιού 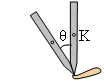 μήκους
12cm στο νύχι του χεριού
μας και φέρνουμε το μολύβι σε κατακόρυφη θέση. Αφήνουμε το μολύβι να πέσει,
οπότε η μύτη του εγκαταλείπει το νύχι σε μια θέση που σχηματίζει γωνία θ
με την κατακόρυφη. Ζητούνται:
μήκους
12cm στο νύχι του χεριού
μας και φέρνουμε το μολύβι σε κατακόρυφη θέση. Αφήνουμε το μολύβι να πέσει,
οπότε η μύτη του εγκαταλείπει το νύχι σε μια θέση που σχηματίζει γωνία θ
με την κατακόρυφη. Ζητούνται:
α) Η γωνία θ.
β) Η γωνιακή ταχύτητα του μολυβιού τη στιγμή που χάνει την επαφή με το νύχι.
γ) Πόση είναι η ταχύτητα του κέντρου Κ του μολυβιού στην παραπάνω θέση;
δ) Δίνεται η ροπή αδράνειας του μολυβιού ως προς κάθετο σε αυτό άξονα που περνά από το μέσον του Κ, που θεωρείται και κέντρο μάζας του μολυβιού Ιcm = 1/12ml2, όπου l το μήκος του.
Υπόδειξη:
Πόση δύναμη δέχεται το μολύβι από το νύχι τη στιγμή που το εγκαταλείπει και τι
ταχύτητα έχει το κέντρο Κ;
Γύρω από ποιο σημείο στρέφεται το μολύβι για όσο χρόνο βρίσκεται σε επαφή με το
νύχι;