Ανδρέας
Ιωάννου Κασσέτας
Οι
λύσεις των προβλημάτων 21- 30
21.Ο πίθηκος είναι νηστικός
Ένα
σκοινί περνάει από μία ακίνητη τροχαλία. Στο ένα του άκρο του είναι δεμένο ένα
τσαμπί με μπανάνες και στο άλλο είναι γαντζωμένος ένας πεινασμένος πίθηκος
χαμηλότερα από τις μπανάνες. Το τσαμπί με τις μπανάνες έχει το ίδιο βάρος με
εκείνο του πιθήκου. Αρχικώς το σύστημα ακινητεί. Ο πίθηκος αρχίζει να σκαρφαλώνει στο σκοινί
προσπαθώντας να φθάσει στο ίδιο ύψος με τις μπανάνες. Η διάμετρος της τροχαλίας είναι τόση ώστε εάν
φθάσει στο ίδιο ύψος με τις μπανάνες, απλώνοντας το χέρι, θα μπορέσει να τις
πιάσει. Θα τα καταφέρει; Θεωρούμε
ότι η μάζα τόσο του σκοινιού όσο και της τροχαλίας είναι αμελητέα.
(στον Κώστα
Σκορδούλη )
Η ΛΥΣΗ
Θεωρούμε
το σύστημα «πίθηκος μάζας m, μπανάνες μάζας m,, τροχαλία αμελητέας μάζας και ακτίνας r , σκοινί αμελητέας μάζας» . Η στροφορμή του συστήματος τη στιγμή που το
σύστημα ακινητεί είναι μηδενική και , κατά την εξέλιξη του φαινομένου, θα διατηρηθεί μηδενική. Καθώς λοιπόν
ανεβαίνει ο πίθηκος - ας υποθέσουμε από δεξιά μεριά όπως κοιτάμε- με ταχύτητα
μέτρου υ, η ( ως προς το 0 ) στροφορμή
του είναι ένα διάνυσμα ίσο με mυr . Για να διατηρείται η στροφορμή
μηδενική πρέπει και οι μάζας m οι
μπανάνες να έχουν στροφορμή ( ως προς το 0 ) ίση κατά μέτρο με εκείνη του
πίθηκου αλλά με αντίθετη κατεύθυνση . Αυτό σημαίνει ότι και αυτές θα ανεβαίνουν
με ταχύτητα μέτρου υ. Τόσο δηλαδή ο πίθηκος
όσο και οι μπανάνες θα ανεβαίνουν με ίσες ταχύτητες και ο πίθηκος δεν θα
καταφέρει να τις πιάσει .
22. Το
δακτυλίδι καθυστερεί.
Ένας
κύλινδρος και ένας δακτύλιος ίσων ακτίνων βρίσκονται το ένα δίπλα στο άλλο σε
κεκλιμένο επίπεδο γωνίας 300 και συγκρατούνται. Τα δύο σώματα
αφήνονται ταυτόχρονα και κυλίονται στην επιφάνεια του κεκλιμένου επιπέδου χωρίς
να ολισθαίνουν. Πόσο θα απέχουν τα
κέντρα μάζας των δύο σωμάτων μετά από ένα δευτερόλεπτο; Τα σώματα είναι
ομογενή. Απ: 41,7 cm.

( στον Λουκά
Κορφιάτη )
Η ΛΥΣΗ
Η
κύλιση του κυλίνδρου αναλύεται σε μεταφορική με την ταχύτητα του κέντρου μάζας
και σε στροφική περί άξονα που περνά από το κέντρο μάζας. Εφαρμόζουμε τον
δεύτερο νόμο της κίνησης για τη
μεταφορική κίνηση mgημθ Τ = macm - όπου Τ η στατική τριβή
- και για τη στροφική κίνηση ΤR = Icmαγων και εφόσον αcm = αγωνR τελικά acm = gημθ/( 1+
Ιcm/mR2 ) .
Το
κέντρο μάζας του σώματος με τη μεγαλύτερη ροπή αδράνειας, δηλαδή του δακτυλίου
( Ιcm= mR2) θα
έχει μικρότερη επιτάχυνση. Ο
κύλινδρος ( Ιcm= ½ mR2 ) θα
προηγηθεί.
Οι
αντίστοιχες επιταχύνσεις των δύο κέντρων μάζας θα είναι acm, δακτ = g/4 και acm, κυλ = g/3
Η
μετατόπιση του κέντρου μάζας του κυλίνδρου το πρώτο δευτερόλεπτο θα είναι 1,677
m και του δακτυλίου 1,25 m. Τα
δύο κέντρα μάζας θα απέχουν 41,7 cm .
23. Ο τροχός στο πεζοδρόμιο.
Πόση ταχύτητα πρέπει να
έχει το κέντρο μάζας του κυλιόμενου, χωρίς ολίσθηση, τροχού ώστε να ανέβει στο
πεζοδρόμιο;
Η ακτίνα του τροχού είναι
28 cm
και το ύψος του ρείθρου 8 cm.

Πόση
πρέπει να είναι η αντίστοιχη ταχύτητα ενός κύβου σε μεταφορική κίνηση - πλευράς ίσης με τη διάμετρο του τροχού ώστε
να ανέβει το ίδιο πεζοδρόμιο; (Σε
αυτή την περίπτωση θεωρούμε ότι στο
σημείο
που θα προσκρούσει ο κύβος υπάρχει ακμή όπως στο σχήμα )

( στον Παναγιώτη
Καραμουσαντά )
Η ΛΥΣΗ
Όταν
προσκρούσει ο τροχός στο πεζοδρόμιο, σε σημείο Α, ασκείται δύναμη στον τροχό
στο σημείο επαφής Α . Εφόσον η, ως προς το Α, ροπή της δύναμης, είναι μηδενική, η ως προς Α στροφορμή διατηρείται.
Εφαρμόζουμε
τη Διατήρηση της στροφορμής ως προς Α και εξισώνουμε την ως προς Α στροφορμή
του τροχού ΠΡΙΝ την πρόσκρουση με την ως προς Α στροφορμή του τροχού μετά την
πρόσκρουση.
Lπριν = mucmd + Icmω, όπου d = 20
cm. O πρώτος όρος mucmd είναι η ως προς Α στροφορμή λόγω της
μεταφορικής κίνησης με την ταχύτητα του
κέντρου μάζας και ο δεύτερος
όρος Icmω η ως προς Α στροφορμή λόγω της στροφικής
κίνησης περί άξονα που περνά από το κέντρο μάζας .
Αξίζει
εδώ να σημειώσουμε πως όταν ένα σώμα όπως ο τροχός εκτελεί στροφική κίνηση περί άξονα που περνά
από το κέντρο μάζας ,
η
στροφορμή ως προς το κέντρο μάζας είναι ίση με τη στροφορμή ως προς οποιοδήποτε
σημείο του επιπέδου.
Μετά
το «κτύπημα» στο σημείο Α , η κίνηση του
τροχού γίνεται στροφική περί Α, με αρχική τιμή γωνιακής ταχύτητας την ω1 οπότε Lμετά = IΑω1 .
mucmd + Icmω = IΑω1 Με
δεδομένα ότι Icm=
½ mR2 IΑ= ½ 3mR2/2 και υcm
= ωR η
προηγούμενη σχέση γίνεται
mucm(d+R/2) = 3mR2ω1/2. (1)
Κατά
την στροφική περί Α κίνηση, η οποία ακολουθεί, διατηρείται η ενέργεια, οπότε
εφαρμόζουμε τη Διατήρηση, εξισώνοντας την ενέργεια ½IΑω12
+ mgR
αμέσως μετά την πρόσκρουση με
την ενέργεια που έχει ο τροχός όταν φθάσει στο ανώτερο ύψος ½IΑωαν2
+ mg(R+h), όπου
h= 8 cm το ύψος του πεζοδρομίου. Η οριακή τιμή
της ωαν για την οποία θα καταφέρεινα «ανέβει» και να μείνει στο
πεζοδρόμιο είναι η μηδενική, οπότε ½IΑω12
+ mgR
= mg(R+h) ή ½IAω12= mgh
και τελικά 3mR2ω12 /4= mgh (2)
Από
τις (1)
και (2)
υπολογίζουμε την ελάχιστη τιμή της ucm του τροχού για την οποία
ανεβαίνει στο πεζοδρόμιο
ucm 2 =
3ghR2/(d+ ½ R)2 ucm = 1,28 m/s = 4,6 km/h
Με ανάλογο τρόπο υπολογίζουμε την ελάχιστη ταχύτητα για την οποία
ο κύβος ανεβαίνει στο πεζοδρόμιο
24. Κι αν αργήσουμε να κόψουμε το νήμα;
Το
ομογενές κιβώτιο μάζας m = 1
kg, έχει βάση πλευράς b = 26 cm, έχει ύψος Η = 70 cm, συνδέεται
με σπάγκο, 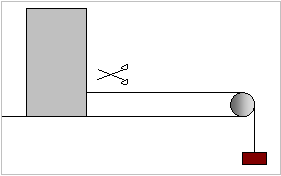 μέσα από τροχαλία, με ένα βαρίδι η μάζα του
οποίου είναι m/2.
Το νήμα προσδένεται στο κιβώτιο σε ύψος 24 cm από την επιφάνεια του τραπεζιού. Αρχικά συγκρατούμε το κιβώτιο
ώστε το σύστημα να ακινητεί και σε κάποια
χρονική στιγμή t= 0 το
αφήνουμε ελεύθερο. Το μέγεθος του τραπεζιού είναι μεγάλων διαστάσεων.
μέσα από τροχαλία, με ένα βαρίδι η μάζα του
οποίου είναι m/2.
Το νήμα προσδένεται στο κιβώτιο σε ύψος 24 cm από την επιφάνεια του τραπεζιού. Αρχικά συγκρατούμε το κιβώτιο
ώστε το σύστημα να ακινητεί και σε κάποια
χρονική στιγμή t= 0 το
αφήνουμε ελεύθερο. Το μέγεθος του τραπεζιού είναι μεγάλων διαστάσεων.
Να
προβλέψετε τι θα συμβεί σε καθεμιά από τις περιπτώσεις:
α.
Ο συντελεστής τριβής είναι 0,7 .
β. Ο συντελεστής τριβής είναι 0, 3 και
κόψουμε το νήμα τη χρονική στιγμή 3 s
Το
κιβώτιο έχει σχήμα ορθογωνίου παραλληλεπιπέδου με αμελητέα την τρίτη διάσταση .
Ο συντελεστής στατικής τριβής είναι ίσος με τον συντελεστή τριβής ολίσθησης .
Τόσο η μάζα της τροχαλίας όσο και η μάζα του νήματος θεωρούνται αμελητέες.
( στον Κώστα
Καλλέργη )
Η ΛΥΣΗ
α. Εάν ο συντελεστής
τριβής είναι 0,7 το κιβώτιο θα μείνει ακίνητο. Η οριζόντια δύναμη από το 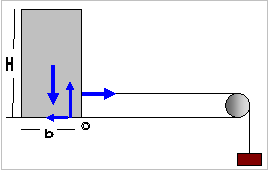 νήμα Fν- κατά τη χρονική εκείνη στιγμή - είναι 0,5 mg και η μέγιστη στατική τριβή είναι 0,7mg
νήμα Fν- κατά τη χρονική εκείνη στιγμή - είναι 0,5 mg και η μέγιστη στατική τριβή είναι 0,7mg
άρα
δεν θα ξεκινήσει για ολίσθηση.
Επίσης
δεν θα ανατραπεί διότι η μέγιστη ροπή της Fν ως προς Ο
είναι ½mg.24/100 Νm = 1,2 Νm και
δεν είναι αρκετή. Η ελάχιστη ροπή που απαιτείται για να αρχίσει να στρέφεται
περί Ο
με
ενδεχόμενο την ανατροπή του είναι mgb/2 = 1,3 Νm.
Το σημείο στο οποίο θα ασκείται η συνολική
κάθετη αντίδραση Ν απέχει 12 cm από το σημείο -προβολή του κέντρου μάζας και 1cm από το άκρο Ο.
β. Εάν ο συντελεστής τριβής είναι 0,3 το κιβώτιο θα
«ξεκινήσει», δεδομένου ότι η εκείνη τη
στιγμή ασκούμενη οριζόντια δύναμη από το νήμα είναι 0,5 mg και η μέγιστη στατική τριβή είναι 0,3mg.
Στη συνέχεια το κιβώτιο συρόμενο από το
τεντωμένο νήμα θα κινείται μεταφορικά με επιτάχυνση 2g/15 και στο τέλος του 3ου
δευτερολέπτου θα έχει αποκτήσει ταχύτητα 4m/s . Αν τη
στιγμή εκείνη κόψουμε το νήμα, το κιβώτιο θα συνεχίσει την μεταφορική  του
κίνηση αλλά με επιβραδύνουσα επιτάχυνση 0,3g = 3m/s2 και θα
σταματήσει σε 4/3s. Η
μεταφορική κίνηση η συνισταμένη όλων των ασκουμένων δυνάμεων διέρχεται από το
κέντρο μάζας και στην περίπτωση αυτή εξασφαλίζεται από το ότι «είναι δυνατόν το
έδαφος να ασκεί τέτοιες δυνάμεις ώστε η ολική ροπή ως προς το κέντο μάζας να
είναι μηδενική» . Η -ως προς το κέντρο μάζας- ροπή της τριβής είναι μmgH/2 = 10,5 Nm και
θα εξισορροπείται από τη ροπή της κάθετης αντίδρασης δεδομένου ότι η μέγιστη
ροπή που μπορεί δημιουργήσει η κάθετη αντίδραση είναι mgb/2 = 1,3 Nm.
του
κίνηση αλλά με επιβραδύνουσα επιτάχυνση 0,3g = 3m/s2 και θα
σταματήσει σε 4/3s. Η
μεταφορική κίνηση η συνισταμένη όλων των ασκουμένων δυνάμεων διέρχεται από το
κέντρο μάζας και στην περίπτωση αυτή εξασφαλίζεται από το ότι «είναι δυνατόν το
έδαφος να ασκεί τέτοιες δυνάμεις ώστε η ολική ροπή ως προς το κέντο μάζας να
είναι μηδενική» . Η -ως προς το κέντρο μάζας- ροπή της τριβής είναι μmgH/2 = 10,5 Nm και
θα εξισορροπείται από τη ροπή της κάθετης αντίδρασης δεδομένου ότι η μέγιστη
ροπή που μπορεί δημιουργήσει η κάθετη αντίδραση είναι mgb/2 = 1,3 Nm.
Η
ολική δύναμη από την επιφάνεια του τραπεζιού δεν θα ασκείται στο άκρο Ο
25. Ο Ηρακλής και το ρόπαλο
 Ο Ηρακλής παίζει με το ρόπαλο.
Επιχειρεί να το ισορροπήσει με το ένα δάκτυλο έτσι ώστε να το διατηρεί
κατακόρυφο. Πώς είναι πιο εύκολο να το πετύχει;
Ο Ηρακλής παίζει με το ρόπαλο.
Επιχειρεί να το ισορροπήσει με το ένα δάκτυλο έτσι ώστε να το διατηρεί
κατακόρυφο. Πώς είναι πιο εύκολο να το πετύχει;
Με το χοντρό μέρος να βρίσκεται προς τα πάνω ή με το χοντρό μέρος
να είναι προς τα κάτω;
Η ΕΜΠΕΙΡΙΑ του λέει να κάνει το πρώτο
αλλά
η ΙΔΕΑ ότι «εάν το κέντρο βάρους είναι ΧΑΜΗΛΑ η ισορροπία θα είναι καλύτερη» του λέει να κάνει το πρώτο.
Τι πρέπει να κάνει; Να εμπιστευτεί την εμπειρική του γνώση ή να
υιοθετήσει την ιδέα;
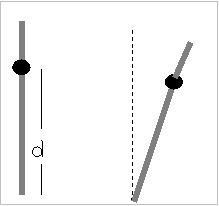 Ρωτήσαμε ένα φυσικό πως θα
μπορούσαμε να το ερευνήσουμε βασιζόμενοι στη
Φυσική και μας συμβούλευσε να επινοήσουμε ένα μοντέλο με γεωμετρική
λογική στο οποίο να εφαρμόσουμε τους φυσικούς νόμους. Φανταστήκαμε λοιπόν μία
μονοδιάστατη ράβδο αμελητέας μάζας
Ρωτήσαμε ένα φυσικό πως θα
μπορούσαμε να το ερευνήσουμε βασιζόμενοι στη
Φυσική και μας συμβούλευσε να επινοήσουμε ένα μοντέλο με γεωμετρική
λογική στο οποίο να εφαρμόσουμε τους φυσικούς νόμους. Φανταστήκαμε λοιπόν μία
μονοδιάστατη ράβδο αμελητέας μάζας
και σε κάποιο σημείο της προσαρμοσμένο ένα σημειακό αντικείμενο
μάζας m σε απόσταση d από τη βάση μεγαλύτερη από το μισό του μήκους της. Και την
φανταστήκαμε αρχικά να ισορροπεί κατακόρυφα με το χέρι μας στη βάση της και στη
συνέχεια να εκτρέπεται από την κατακόρυφο κατά γωνία φ. Ένας τρόπος να κρίνουμε
το κατά πόσο είναι εύκολο να ανατραπεί είναι να υπολογίσουμε τη ΓΩΝΙΑΚΗ
ΕΠΙΤΑΧΥΝΣΗ σε στιγμή που έχει εκτραπεί κατά γωνία φ για να διαπιστώσουμε έτσι
ότι η βασιζόμενη στην ΕΜΠΕΙΡΙΑ υποψία μας είναι βάσιμη. Πώς θα το καταφέρουμε;
Το
πρόβλημα γίνεται λίγο πιο δύσκολο εάν χρησιμοποιήσουμε ομογενή ράβδο μάζας Μ.
( στη Λία
Χαλκιά )
Η ΛΥΣΗ
Θεωρούμε
τη μονοδιάστατη ράβδο με το προσαρμοσμένο αντικείμενο σε απόσταση d από το
κάτω άκρο- να βρίσκεται σε θέση που να σχηματίζει μια μικρή γωνία φ με την
κατακόρυφο και αναζητούμε απάντηση στο ερώτημα «από τι εξαρτάται η ΓΩΝΙΑΚΗ
ΕΠΙΤΑΧΥΝΣΗ, τη στιγμή εκείνη.
Εφαρμόζουμε
στο «σύστημα ράβδος-αντικείμενο» τον νόμο του Νεύτωνα για τη στροφική κίνηση.
0λική ροπή = ροπή αδράνειας x γωνιακή επιτάχυνση
mgdημφ = md 2 αγων άρα αγων = gημφ/d.
Με το να
εμπιστευτούμε δηλαδή τον νόμο του Νεύτωνα διαπιστώνουμε ότι για δεδομένη γωνία
φ η τιμή της γωνιακής επιτάχυνσης είναι αντιστρόφως ανάλογη με το ύψος στο
οποίο βρίσκεται το κέντρο μάζας
Το καλύτερο που έχει να κάνει ο Ηρακλής
είναι να εμπιστευθεί την ΕΜΠΕΙΡΙΑ διότι η ΙΔΕΑ που αναφέρεται στη θέση του
κέντρου βάρους αγνοεί τον ρόλο της ροπής αδράνειας .
26. Η άσπρη κιμωλία και η κόκκινη κιμωλία
Δύο
κιμωλίες όμοιες πάνω σε θρανίο για το οποίο έχουμε μεριμνήσει ώστε να είναι
κεκλιμένο επίπεδο γωνίας θ. Τη  μία κιμωλία, την κόκκινη, τη συγκρατούμε έτσι ώστε ο άξονας της να
είναι παράλληλος προς το κεκλιμένο και να σχηματίζει με τον ορίζοντα γωνία
θ. Αν την αφήσουμε ελεύθερη θα ολισθήσει
σε μεταφορική κίνηση. Η άσπρη κιμωλία
συγκρατείται στο χαμηλότερο σημείο της κόκκινης με τον άξονά της κάθετο στον
άξονα της πρώτης και αν την αφήσουμε θα κυλήσει χωρίς ολίσθηση.
μία κιμωλία, την κόκκινη, τη συγκρατούμε έτσι ώστε ο άξονας της να
είναι παράλληλος προς το κεκλιμένο και να σχηματίζει με τον ορίζοντα γωνία
θ. Αν την αφήσουμε ελεύθερη θα ολισθήσει
σε μεταφορική κίνηση. Η άσπρη κιμωλία
συγκρατείται στο χαμηλότερο σημείο της κόκκινης με τον άξονά της κάθετο στον
άξονα της πρώτης και αν την αφήσουμε θα κυλήσει χωρίς ολίσθηση.
Εάν
τις αφήσουμε ταυτόχρονα μπορούμε, βάσει φυσικών νόμων, να προβλέψουμε ότι η
άσπρη θα φθάσει πρώτη κάτω;
Μπορούμε
επίσης να αποδείξουμε ότι
α.
για να συμβεί η ΜΕΤΑΦΟΡΙΚΗ ΚΙΝΗΣΗ της
κόκκινης πρέπει να ισχύει μ < εφθ
β.
για να συμβεί η ΚΥΛΙΣΗ ΧΩΡΙΣ ΟΛΙΣΘΗΣΗ
της άσπρης πρέπει να ισχύει μσ
> εφθ/3 και
γ.
εφόσον εφθ > μ > εφθ/3 η κυλιόμενη λευκή θα φθάσει πρώτη κάτω.
Το
μσ παριστάνει τον συντελεστή στατικής τριβής και το μ τον συντελεστή
τριβής ολίσθησης
( στον Παντελή
Λαρεντζάκη )
Η ΛΥΣΗ

α. Για την κόκκινη
κιμωλία. Έστω ότι ισορροπεί. mgημθ= Τσ
και mgσυνθ = Ν
Επίκειται ολίσθηση
εφόσον Τσ = μσΝ mgημθ = μσmgσυνθ
ή μσ
= εφφ
β. Για την άσπρη κιμωλία
Υποθέτουμε ότι κυλίεται χωρίς ολίσθηση. Σύμφωνα με
τον δεύτερο νόμο τόσο για τη μεταφορική όσο και για τη στροφική κίνηση ισχύει
mgημθ-
Τσ = macm .
Τσ
R = Icm. aγων . Αλλά
Icm. = ½ mR2 και acm = aγωνR
οπότε acm = 2gημθ/3 και
Τσ = 1/3. mgημθ
Για
να γίνεται η κύλιση χωρίς ολίσθηση πρέπει Τσ ≤ μ Ν
Και
εφόσον Ν = mgσυνθ 1/3. mgημθ ≤ μ mgσυνθ εφθ/3 ≤ μ

γ. Εφόσον εφθ
> μ > εφθ/3 η μεν κόκκινη θα
ολισθήσει. Η
ολίσθηση είναι μεταφορική κίνηση για την οποία mgημφ-μΝ= ma και Ν = mgσυνθ
’ρα η επιτάχυνση της κόκκινης θα είναι ακοκ =g(ημθ-μσυνθ)
Η λευκή θα κυλίσει με επιτάχυνση του κέντρου μάζας η οποία
υπολογίστηκε προηγουμένως και είναι
acmλευκής
= 2gημθ/3 Για να ισχύει acmλευκής >
ακοκ
μ > εφθ/3
2gημθ/3 > g(ημθ-μσυνθ) αρκεί να είναι μ > εφθ/3
27. Κάθε σημείο και διαφορετική ταχύτητα
 Πιάνουμε με το χέρι ένα τετράγωνο
χαρτόνι ΑΒΓΔ και το εκτοξεύουμε πάνω στο
τραπέζι. Η κίνηση που κάνει δεν είναι μεταφορική. Σέρνεται πάνω στο τραπέζι και
στρίβει ταυτόχρονα. Αν ξέρουμε ότι σε κάποια χρονική στιγμή η ταχύτητα του σημείου Α έχει μέτρο υ και κατεύθυνση προς το κέντρο του
τετραγώνου και ότι η διεύθυνση της
ταχύτητας του Γ είναι κατά την ευθεία ΒΓ μπορούμε να προσδιορίσουμε τις
ταχύτητες των Β, Δ και Γ. Πώς θα γίνει αυτό;
Πιάνουμε με το χέρι ένα τετράγωνο
χαρτόνι ΑΒΓΔ και το εκτοξεύουμε πάνω στο
τραπέζι. Η κίνηση που κάνει δεν είναι μεταφορική. Σέρνεται πάνω στο τραπέζι και
στρίβει ταυτόχρονα. Αν ξέρουμε ότι σε κάποια χρονική στιγμή η ταχύτητα του σημείου Α έχει μέτρο υ και κατεύθυνση προς το κέντρο του
τετραγώνου και ότι η διεύθυνση της
ταχύτητας του Γ είναι κατά την ευθεία ΒΓ μπορούμε να προσδιορίσουμε τις
ταχύτητες των Β, Δ και Γ. Πώς θα γίνει αυτό;
( στον Πέτρο
Μιχαλακάκο )
Η ΛΥΣΗ
Μπορούμε να το
αντιμετωπίσουμε με δύο τρόπους που αντιστοιχούν στις δύο διαφορετικές θεωρήσεις
της κίνησης ενός σώματος.
Ο πρώτος.
Να θεωρήσουμε την κίνηση του χαρτονιού
ως ΣΤΡΟΦΙΚΗ ΠΕΡΙ  ΣΤΙΓΜΙΑΙΟ
ΑΞΟΝΑ και να
ΣΤΙΓΜΙΑΙΟ
ΑΞΟΝΑ και να
προσδιορίσουμε
τη θέση του άξονα τη στιγμή εκείνη. Για
τον σκοπό αυτό φέρνουμε μια κάθετο στην ευθεία της ταχύτητας υ του σημείου Α
και μια άλλη κάθετο στην ευθεία της
ταχύτητας του σημείου Γ.
Το σημείο
τομής 0 των δύο καθέτων είναι το σημείο από το οποίο διέρχεται ο στιγμιαίος
άξονας περιστροφής του σώματος.
Οι τιμές
των ταχυτήτων θα είναι
υΑ(υ)
= ω(ΟΑ),
υΒ = ω(ΟΒ), υΓ = ω(ΟΓ)
και υΔ = ω(ΟΔ),
όπου ω
η στιγμιαία ταχύτητα της περί Ο περιστροφής.
Από τη
Γεωμετρία και την Τριγωνομετρία μπορούμε να συμπεράνουμε ότι
ΟΑ =√2α ΟΒ =√5α ΟΓ = 2α και ΟΔ
= α , όπου α η
πλευρά του τετραγώνου , οπότε καταλήγουμε στο ότι
υΒ = υ√5/√2 , υΓ = υ√2 και υΔ = υ/√2
Η διεύθυνση
της υΒ είναι κάθετη στην ΟΒ και η διεύθυνση της υΔ κάθετη
στην ΟΔ
Ο δεύτερος
τρόπος. Να θεωρήσουμε την κίνηση του
χαρτονιού ως σύνθεση
 μιας
μεταφορικής με την
ταχύτητα υcm του κέντρου μάζας και μιας στροφικής περί άξονα, κάθετο στο επίπεδο του
σχήματος,ο οποίος διέρχεται από το κέντρο μάζας Κ.
μιας
μεταφορικής με την
ταχύτητα υcm του κέντρου μάζας και μιας στροφικής περί άξονα, κάθετο στο επίπεδο του
σχήματος,ο οποίος διέρχεται από το κέντρο μάζας Κ.
28. Τα μυρμήγκια μετακινούν το ξυλαράκι
 Σε εντυπωσιακή συνεργασία τα
μυρμήγκια μετακινούν το ξυλαράκι ΖΗ. Πρόκειται για μια τυχαία κίνηση.
Σε εντυπωσιακή συνεργασία τα
μυρμήγκια μετακινούν το ξυλαράκι ΖΗ. Πρόκειται για μια τυχαία κίνηση.
Το άκρο Ζ έχει ταχύτητα
μέτρου υ το διάνυσμα της οποίας σχηματίζει γωνία φ με τον άξονα ΖΗ.
Το άκρο Η έχει
ταχύτητα άγνωστου μέτρου η διεύθυνση της οποίας σχηματίζει γωνία θ με την
ευθεία ΖΗ.
Πώς
μπορούμε να υπολογίσουμε το μέτρο της ταχύτητας του άκρου Η ; ( από το
περιοδικό QUANTUM)
( στην Πανδώρα
Χατζηδάκη )
Η
ΛΥΣΗ
Μπορούμε να το
αντιμετωπίσουμε με δύο τρόπους που αντιστοιχούν στις δύο διαφορετικές θεωρήσεις
της κίνησης ενός σώματος.
Ο πρώτος.
Να θεωρήσουμε την κίνηση του σώματος ΖΗ ως ΣΤΡΟΦΙΚΗ ΠΕΡΙ
ΣΤΙΓΜΙΑΙΟ ΑΞΟΝΑ και να  προσδιορίσουμε
τη θέση του άξονα τη στιγμή εκείνη. Για
τον σκοπό αυτό φέρνουμε μια κάθετο στην ευθεία της ταχύτητας υ του σημείου Ζ
και μια άλλη κάθετο στην ευθεία της
ταχύτητας του σημείου Η.
προσδιορίσουμε
τη θέση του άξονα τη στιγμή εκείνη. Για
τον σκοπό αυτό φέρνουμε μια κάθετο στην ευθεία της ταχύτητας υ του σημείου Ζ
και μια άλλη κάθετο στην ευθεία της
ταχύτητας του σημείου Η.
Το σημείο τομής
0 των δύο καθέτων είναι το σημείο από το οποίο διέρχεται ο στιγμιαίος άξονας
περιστροφής του σώματος. Η τιμές των δύο ταχυτήτων θα είναι υΗ =
ω(ΟΗ) και υΖ = ω(ΟΖ) όπου ω η στιγμιαία ταχύτητα της περί Ο
περιστροφής. Ισχύει συνεπώς υΗ /υΖ = (ΟΗ)/(ΟΖ)
Ο λόγος
υπολογίζεται από τη σχέση των ημιτόνων στο τρίγωνο ΟΖΗ.
(ΟΗ)/(ΟΖ)= ημ(
90-φ)/ημ(90+θ) = συνφ/συνθ . Τελικά υΗ = υσυνφ/συνθ
Ο δεύτερος. Να
θεωρήσουμε την κίνηση του σώματος (μήκους L = ΖΗ) ως σύνθεση μιας μεταφορικής με την ταχύτητα υcm
του κέντρου μάζας και μιας στροφικής περί άξονα, κάθετο στο επίπεδο του
σχήματος,
 ο οποίος διέρχεται από το κέντρο μάζας Κ, στο
μέσον του ΖΗ.
ο οποίος διέρχεται από το κέντρο μάζας Κ, στο
μέσον του ΖΗ.
Για την
ταχύτητα υ του σημείου Η ισχύει
|
|
από
την οποία προκύπτουν οι αλγεβρικές σχέσεις
υημφ = υcmx + ωL /2
και υσυνφ = υcmy
όπου
ω η γωνιακή ταχύτητα της στροφικής κίνησης περί το κέντρο μάζας
Από
την αντίστοιχη σχέση για την ταχύτητα
του σημείου Η
|
|
προκύπτουν
οι αλγεβρικές σχέσεις
υHημθ = υcmx
- ωL /2 και υH συνθ = υcmy
Από τις τέσσερεις αλγεβρικές σχέσεις θα
χρειαστούμε τις δύο, την υσυνφ
= υcmy και
την υH συνθ = υcmy
για για να συμπεράνουμε ότι υΗ = υσυνφ/συνθ.
Από τις άλλες δύο μπορούμε να υπολογίσουμε τηνταχύτητα του κέντρου
μάζας και τη γωνιακή ταχύτητα
29. Το βλήμα σε μεταφορική και στροφική κίνηση
Το
βλήμα έχει μάζα m και
κατευθύνεται προς τον στόχο του έχοντας και στροφική κίνηση περί τον άξονά του.
Σε κάθε πλήρη περιστροφή το κέντρο μάζας του μετακινείται κατά 84π cm. Να υπολογίσετε πόσες φορές μεγαλύτερη
είναι η κινητική του ενέργεια λόγω μεταφοράς από την κινητική ενέργεια λόγω
περιστροφής.
Η
ροπή αδράνειας του βλήματος ως προς άξονα που περνάει από το κέντρο μάζας είναι
ίση με τη ροπή αδράνειας
ενός
δακτυλίου μάζας m
και ακτίνας R = 12 cm.
( στον Γιώργο
Μωραΐτη )
Αν συμβολίσουμε με λ το
ζητούμενο «πόσες φορές» θα είναι Κμετ = λΚπερ
½mυcm2
= λ ½mR2ω2 άρα λ = (υcm/ωR)2
Κάθε περιστροφή
ολοκληρώνεται σε χρόνο t
για τον οποίο 2π = ωt
Στη χρονική αυτή
διάρκεια το κέντρο μάζας θα έχει μετατοπιστεί κατά d = 84π cm. ’ρα d = υcm t.
Προκύπτει ότι υcm /ω
= d/2π
οπότε λ = (υcm/ωR)2 = (d/2πR)2 = 12,25
30. Η σανίδα και οι κύλινδροι
Η
πρισματική σανίδα έχει μάζα m, βρίσκεται πάνω σε δύο κυλίνδρους και σύρεται
σε μεταφορική κίνηση με οριζόντια δύναμη F ίση με το ¼ του βάρους της. Οι δύο
κύλινδροι - καθένας τους μάζας ½m -κυλίονται
χωρίς ολίσθηση σε οριζόντιο έδαφος, Να προσδιορίσετε την επιτάχυνση της
σανίδας.

(Απάντηση
: 2g/11)
( στον Βασίλη
Δικαιουλάκο )
Η
ΛΥΣΗ
Για το σώμα
«ένας κύλινδρος» το οποίο κυλίεται χωρίς ολίσθηση ισχύει

F1+T = mκυλ.αcm,κυλ ( 1)
F1R TR
= Icm αγων ή F1R
TR = ½ mR2 αγων
ή F1 T = ½mκυλαcm,κυλ ( 2)
Από τις (1) και (2) F1 = ¾ mκυλαcm,κυλ . Η επιτάχυνση του
κέντρου μάζας του κυλίνδρου είναι το μισό της επιτάχυνσης του ανώτερου σημείου
του κυλίνδρου άρα ίση συνεπώς με το της επιτάχυνσης της σανίδας αcm,κυλ = ½ ασαν
Με δεδομένο ότι mκυλ= m/2 η τιμή της θα είναι F1 = 3/16mασαν
Για το σώμα
«σανίδα» το οποίο κινείται μεταφορικά.

Οι ασκούμενες στη σανίδα δυνάμεις είναι η οριζόντια F
= mg/4 , η
δύναμη από τον ένα κύλινδρο ίση κατά μέτρο με την F1 αλλά με αντίθετη
κατεύθυνση νόμος δράσης αντιδρασης και μια ακόμα από τον άλλο κύλινδρο ίση
με την προηγούμενη
F - 2F1 = m.ασαν και λόγω της σχέσης (3) mg/4 - 3/8mασαν = mασαν
ασαν= 2g/11