Reconstruction OF
A CROP CIRCLE
”Crop circle s
Crop
circles (in French : les agroglyphes, in German : Kornkreise) are geometric,
non-geometric or random figures in crops or vegetation. They appear in the form
of one simple circle, multiple circles or more extensive and complicated
patterns. The dimensions of crop circles differ too. Simple circles can have a
diameter of just a few metres but the more complicated patterns can be as big
as several football fields. These figures are most commonly witnessed in the
South of England, in areas close to old places of worship like
The
picture below is a corn circle found on

Many
patterns of crop circles show such an
intriguing structure that they are simply waiting to be discovered. The purpose
of this article is not to find out how crop circles are being made. The
internet offers a lot of information (but unfortunately also a lot of nonsense)
on this subject. Theories about the origin of the circles differ : some see
them as messages of aliens, others think they are produced by well organised circle
makers (hoaxes), still others think they are the result of exceptional weather
conditions.
This
article concentrates on the mathematical patterns that are hidden behind the
crop circle structures and wants to support the willingness to discover the
underlying mathematical patterns that enhance the fascination for the artistic
beauty of the patterns.
“Construction
with compass and ruler” seems to be a particularly efficient tool for these
reconstructions but modern geometry software offers us precision, unknown
before. One thing cannot be denied : the makers of crop circles must have a
sound knowledge of geometry.
On
the next page the Bishop Cannings circle is being meticulously reconstructed,
step by step, using the GeoGebra geometry software.
|
|
|
|
|
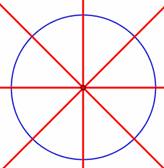
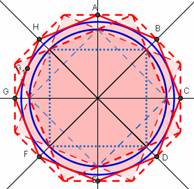
Draw
a circle. |
Draw 4 centerlines at 45°. |
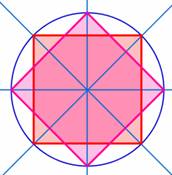
Construct two
squares. |
|
|
|
|
|
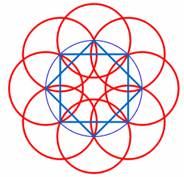
Draw eight
circles, centered at the corners of the squares, and passing through the
adjacent corners. |
Construct two
larger squares through the corners of the smaller ones as shown. |
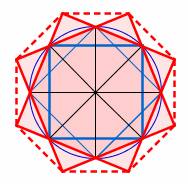
Construct a
large octagon by connecting the corners of the larger squares. |
|
|
|
|
|
From the
endpoints of the centerlines, construct again an octagon, inscribed in the
large one. |
The outer border
of the ring is formed by a circle, inscribed in the octagon of the previous
step. |
Construct the
arcs as shown and remove all the
superfluous parts |
Try to reconstruct another crop circle in a similar
way. Note down all the steps you take and use GeoGebra. It can be downloaded,
completely free of charge, from www.geogebra.at.
The most interesting creations might be published on the websites of the European Com@net project, http://www.vivante.it/com@net , http://www.math.be or http://users.sch.gr/dkastani/encrop.html