Απόλυτα – mathland

ΑΛΓΕΒΡΑ Α΄ ΛΥΚΕΙΟΥ

Για το πως μπορούμε να απαλλαγούμε από τις απόλυτες τιμές που τυχόν εμφανίζονται σε μία αλγεβρική παράσταση έχουμε αναφερθεί σε προηγούμενο άρθρο μας (και καλό θα ήταν να του ρίξετε μια ματιά κάνοντας κλικ εδώ). Σε αυτή τη δημοσίευση θα ασχοληθούμε με εξισώσεις στις οποίες ο άγνωστος βρίσκεται πίσω από τις μπάρες της απόλυτης τιμής. Εξισώσεις δηλαδή που ο άγνωστος είναι «φυλακισμένος» μέσα σε μία ή και περισσότερες απόλυτες τιμές. Σκοπός μας σε μια τέτοια εξίσωση (όπως και σε κάθε εξίσωση άλλωστε) είναι να βρούμε ποιος αριθμός είναι «κρυμμένος πίσω από τη μάσκα του x». Στόχος μας είναι να «ελευθερώσουμε» το x μέσα από την απόλυτη τιμή. Για να το καταφέρουμε αυτό ας θυμηθούμε πρώτα τι είναι η απόλυτη τιμή ενός αριθμού και μετά βλέπουμε πως λύνουμε την εξίσωση.

Η απόλυτη τιμή ενός αριθμού ορίζεται και αλγεβρικά και γεωμετρικά. Εμείς θα αρκεστούμε στο δεύτερο μιας και είναι αρκετό για να στηριχτούμε σε αυτό και να καταφέρουμε να λύσουμε τις εξισώσεις.

Τι είναι λοιπόν η απόλυτη τιμή;

Γνωρίζουμε ότι κάθε πραγματικός αριθμός x παριστάνεται με ένα σημείο πάνω στον άξονα των πραγματικών αριθμών. Την απόσταση του σημείου αυτού από το 0 τη λέμε απόλυτη τιμή του αριθμού x και τη συμβολίζουμε |x|.

absolute — Η απόλυτη τιμή ενός αριθμού εκφράζει την απόστασή του από το 0, χωρίς να μας ενδιαφέρει η σχετική του θέση αν δηλαδή βρίσκεται πριν ή μετά το 0

Έτσι μπορούμε να εξηγήσουμε και πολλές από τις ιδιότητες της απόλυτης τιμής όπως

Η απόλυτη τιμή οποιουδήποτε αριθμού είναι είτε θετικός αριθμός είτε μηδέν, γιατί όπως είναι γνωστό αρνητική απόσταση δεν υπάρχει. Έτσι έχουμε,
$|x|\geq0$

Οι αντίθετοι αριθμοί έχουν την ίδια απόλυτη τιμή, αφού ισαπέχουν από το 0.
$|-x|=|x|$

Ας δούμε τώρα τι γίνεται με τις εξισώσεις.

Σας θυμίζω ότι για να αντιλαμβανόμαστε καλύτερα τις εξισώσεις μπορούμε να τις θεωρούμε σαν ερωτήσεις. Έτσι η εξίσωση |x|= -5 , μας ρωτάει ποιος αριθμός είναι αυτός που απέχει από το 0 -5 μονάδες; Προφανώς η απάντηση είναι κανένας (αναφέραμε και πιο πάνω ότι δεν νοείται αρνητική απόσταση). Ενώ η απάντηση στην ερώτηση(=εξίσωση) |x|=0 είναι «ο μοναδικός αριθμός που απέχει από το μηδέν 0 μονάδες είναι ο 0». Όμως η εξίσωση |χ|=2 μας ζητάει να βρούμε τον αριθμό που απέχει από το 0 2 μονάδες. Η απάντηση είναι ότι δεν υπάρχει μόνο ένας αριθμός με αυτή την ιδιότητα αλλά δύο αριθμοί ο 2 και ο -2. Έτσι η εξίσωσή μας έχει δύο λύσεις τις x=2 ή x= -2. Για να γενικεύσουμε λίγο τα πράγματα και να τα βάλουμε σε μία τάξη δείτε το παρακάτω σχεδιάγραμμα.

Εξισώσεις με απόλυτα — Προσοχή! Όταν a>0 έχουμε 2 λύσεις

Όπου βλέπετε f(x) θα εννοούμε «μια παράσταση που περιέχει x». Γιατί μέσα στο απόλυτο δεν είναι απαραίτητο να υπάρχει μόνο x, μπορεί κάποιοι «κακοί μαθηματικοί» (σαν κι εμένα) να ζητήσουν να λυθούν εξισώσεις που μέσα στο απόλυτο να υπάρχουν αρκετά πράγματα.

Για να λύσουμε οποιαδήποτε εξίσωση στην οποία το x βρίσκεται μέσα σε απόλυτο, πρέπει να στηριχτούμε στα συμπεράσματα του παραπάνω πίνακα. Πρέπει λοιπόν να απομονώσουμε το απόλυτο στο ένα μέλος και μετά κοιτώντας τι ρόλο παίζει το άλλο μέλος να αποφανθούμε αν η εξίσωση έχει λύσεις ή όχι και στην περίπτωση που έχει ποιες είναι αυτές. Ας δούμε τώρα μερικά παραδείγματα:

Άσκηση 1: Να λυθεί η εξίσωση 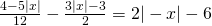$\frac{4-5|x|}{12}-\frac{3|x|-3}{2}=2|-x|-6$

[gn_spoiler title=»Λύση:»]Φαίνεται η εξίσωση μας να έχει δύο διαφορετικές απόλυτες τιμές την |x| και την |-x|. Αυτό όμως δεν αληθεύει γιατί ξέρουμε ότι |-x|=|x|. Οπότε μπορούμε στην εξίσωση που μας δώσανε όπου έχει |-x| εμείς να βάλουμε |x|. Για να απομονώσουμε το απόλυτο που θέλουμε θα ακολουθήσουμε τη γνωστή διαδικασία που ακολουθούμε σε όλες τις εξισώσεις α΄ βαθμού.
Πρώτα θα διώξουμε τους παρονομαστές πολλαπλασιάζοντας κάθε όρο με το Ε.Κ.Π. των παρονομαστών που είναι το 12

$12\frac{4-5|x|}{12}-12\frac{3|x|-3}{2}=12\cdot 2|x|-12\cdot 6 \Leftrightarrow$

$4-5|x|-6(3|x|-3)=24|x|-72$

Τώρα διώχνουμε τις παρενθέσεις κάνοντας χρήση της επιμεριστικής ιδιότητας

$4-5|x|-18|x|+18=24|x|-72$

Χωρίζουμε τους γνωστούς από τους άγνωστους ώστε να μπορέσουμε να συνεχίσουμε τις πράξεις χωρίς να ξεχνάμε ότι προς το παρόν άγνωστος είναι το |x| κι όχι το x

$-5|x|-18|x|-24|x|=-4-18-72\Leftrightarrow$

$-47|x|=-94\Leftrightarrow 47|x|=94$

άρα

$|x|=\frac{94}{47}$

ή πιο απλά

$|x|=2$

Αφού καταφέραμε κι απομονώσαμε το απόλυτο μπορούμε σύμφωνα με όσα έχουμε πει πιο πάνω ν΄απαντήσουμε ότι $x=2$ ή $x=-2$
[/gn_spoiler]

Άσκηση 2: Να λυθεί η εξίσωση 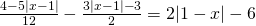$\frac{4-5|x-1|}{12}-\frac{3|x-1|-3}{2}=2|1-x|-6$

[gn_spoiler title=»Λύση:»]Όπως θα παρατηρήσατε η εξίσωση αυτή είναι ίδια με την προηγούμενη με την μόνη αλλαγή αντί για |x| έχουμε |x-1|. Και πάλι επειδή οι αριθμοί 1-x και x-1 είναι αντίθετοι η εξίσωση θα γίνει

$\frac{4-5|x-1|}{12}-\frac{3|x-1|-3}{2}=2|x-1|-6$

και θα λυθεί με τον ίδιο ακριβώς τρόπο καταλήγοντας στο

$|x-1|=2 \Leftrightarrow\left\{\begin{matrix}x-1=-2\Leftrightarrow x=-2+1=-1\\ \eta\\x-1=2\Leftrightarrow x=2+1=3\end{matrix}$

Έτσι λοιπόν βλέπουμε ότι αν τα απόλυτα που έχουμε στην εξίσωση περιέχουν ίσες ή ακόμη και αντίθετες παραστάσεις, τότε δεν μας ενδιαφέρει το περιεχόμενη της απόλυτης τιμής. Λύνουμε την εξίσωση κανονικά όπως όλες τις εξισώσεις «κουβαλώντας» το απόλυτο μέχρι να καταφέρουμε να το απομονώσουμε και στο τέλος το πετάμε (πάντα σύμφωνα με το διάγραμμα που έχουμε παραπάνω).
Επειδή κάποιοι μπορεί να «ψιλό» μπερδεύονται κουβαλώντας το απόλυτο μπορούν να γλυτώσουν από αυτό με την συνηθισμένη στα μαθηματικά μέθοδο: «αν κάτι μ΄ενοχλεί κάνω πως δεν το βλέπω». Έτσι λοιπόν θα μπορούσαμε να θέσουμε όπου |x-1|=α (σχέση 1) και να λύσουμε την εξίσωση χωρίς το απόλυτο. Μόλις ξεμπερδέψουμε με το α και το βρούμε γυρίζουμε και το αντικαθιστούμε στη σχέση 1 απ’ όπου υπολογίζουμε το x που μας ενδιαφέρει.
Watch me
Θέτω |χ-1|=α (σχέση 1) οπότε η εξίσωση γίνεται

$\frac{4-5a}{12}-\frac{3a-3}{2}=2a-6\Leftrightarrow$

$12\frac{4-5a}{12}-12\frac{3a-3}{2}=12\cdot 2a-12\cdot 6 \Leftrightarrow$

$4-5a-6(3a-3)=24a-72\Leftrightarrow$

$-5a-18a-24a=-4-18-72\Leftrightarrow$

$-47a=-94\Leftrightarrow a=2$

Ας μην ξεχνάμε όμως ότι δεν ψάχναμε το α αλλά το x. Πάμε λοιπόν στη σχέση 1 και αντικαθιστούμε όπου α=2, οπότε

$|x-1|=a \Leftrightarrow|x-1|=2 \Leftrightarrow\left\{\begin{matrix}x-1=-2\Leftrightarrow x=-2+1=-1\\ \eta\\x-1=2\Leftrightarrow x=2+1=3 \end{matrix}$

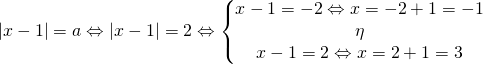
Τη μέθοδο αυτή για να είμαι ειλικρινής δεν σας την έδειξα μόνο για την περίπτωση που κάποιος δυσκολεύεται με τα πολλά απόλυτα αλλά και γιατί σε κάποιες περιπτώσεις θα έλεγα δεν μπορούμε να την αποφύγουμε γι’ αυτό καλό είναι να την ξέρουμε. Δείτε την επόμενη άσκηση και θα καταλάβετε. [/gn_spoiler]

Άσκηση 3: Να βρεθούν οι αριθμοί που ικανοποιούν τη σχέση 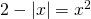$2-|x|=x^2$

[gn_spoiler title=»Λύση:»] Την άσκηση αυτή θα μπορούσαμε να τη λύσουμε απομονώνοντας το απόλυτο στο ένα μέλος, οπότε η εξίσωση να γίνει |x|=2 – x² αλλά πιστεύω ότι έτσι δεν θα μας συνέφερε γιατί το δεύτερο μέλος (το 2 – x²) δεν γνωρίζουμε αν είναι θετικός ή αρνητικός αριθμός ( για κάποιες τιμές του x γίνεται θετικός, για κάποιες αρνητικός και για κάποιες γίνεται ίσος με 0). Έτσι θα έπρεπε να διακρίνουμε περιπτώσεις και να πούμε

Περίπτωση 1η: αν το 2 – x² είναι αρνητικό η εξίσωσή μας είναι αδύνατη (βλέπε και το σχεδιάγραμμα πιο πάνω)

Περίπτωση 2η: αν $2 - x^2\geq0$ , τότε x=2-x² ή x= – (2-x²) και να λύσω δύο εξισώσεις (δεύτερου βαθμού η καθεμία) κι αφού βρω τις λύσεις να κρατήσω από αυτές μόνο εκείνες που επαληθεύουν τον περιορισμό $2 - x^2\geq0$ .

Για να γλυτώσουμε όλη αυτή τη δουλειά μπορούμε να σκεφτούμε λίγο πιο έξυπνα και να αντικαταστήσουμε το |x| με έναν άλλο αριθμό έστω α. Τότε θα έχουμε γλυτώσει και από το |x| αλλά και από το x² γιατί το x²=|x²|=|x|²=α² (ρίξε μια ματιά στις ιδιότητες των απολύτων). Ας δούμε τώρα πως έχει καταντήσει η εξίσωσή μας θέτοντας |x|=α,

$2-a=a^2\Leftrightarrow a^2+a-2=0$

Η διακρίνουσα του τριωνύμου είναι

$\Delta=1^2-4(-2)=9$

και οι λύσεις της εξίσωσης αυτής είναι

$a=1$

$a=-2$

Εύκολα λοιπόν βρήκαμε το α, το x όμως είναι αυτό που μας ενδιαφέρει

$\left | x \right |=\alpha \Leftrightarrow \left\{\begin{matrix} \left | x \right |=1 \Leftrightarrow x=\pm 1\\\eta'\\ \left | x \right |=-2 & \alpha \delta \upsilon \nu \alpha \tau \eta \end{matrix}\right.$

[/gn_spoiler]

Άσκηση 4: Να βρεθούν οι αριθμοί που ικανοποιούν τη σχέση 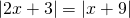$|2x+3|=|x+9|$

[gn_spoiler title=»Λύση:»] Στην άσκηση αυτή ανήκει στη γενική κατηγορία

$|f(x)|=|g(x)|$

και λύνεται με την ισοδυναμία

$|f(x)|=|g(x)| \Leftrightarrow \left\{\begin{matrix}f(x)=g(x)\\ \eta\\f(x)=-g(x) \end{matrix}$

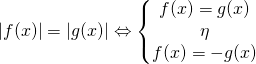
Έχουμε λοιπόν 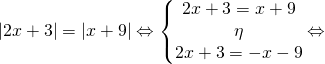$|2x+3|=|x+9| \Leftrightarrow \left\{\begin{matrix}2x+3=x+9\\ \eta\\2x+3=-x-9 \end{matrix}\Leftrightarrow$

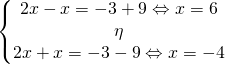$\left\{\begin{matrix}2x-x=-3+9\Leftrightarrow x=6\\ \eta\\2x+x=-3-9\Leftrightarrow x=-4 \end{matrix}$ [/gn_spoiler]

Ετικέτα: Απόλυτα

Θέλω να μάθω … να λύνω εξισώσεις με απόλυτα