Ας δούμε λοιπόν το πλαίσιο ...

• Ο βασιλιάς Πύρρος επιστρέφει από την Ιταλία έχοντας ουσιαστικά αποτύχει στην εκστρατεία του.

• Η Ρώμη έχει καταλάβει την κεντρική Ιταλία και επεκτείνεται σταδιακά στις Ελληνικές πόλεις του νότου.

• Στην Αίγυπτο βασιλεύει ο Πτολεμαίος ο Β' ο φιλάδελφος (δηλαδή αυτός που αγαπά την αδελφή του μια και μέσα από μια ιστορία με ίντριγκες και δολοφονίες βρέθηκε παντρεμένος με την ομόαιμη αδελφή του την Αρσινόη).

• Στην Ινδία βασιλεύει ένας φωτισμένος μονάρχης ο Ασόκα.

• Δεν μπορούμε να πούμε το ίδιο για την Κίνα όπου Σιχ Χουόνγκ Τι στα πλαίσια των μεταρρυθμίσεών του , για να γίνει μια νέα αρχή , δίνει εντολή να καταστραφούν όλα τα γραπτά κείμενα , με εξαίρεση αυτά που αναφέρονται στις πρακτικές τέχνες.

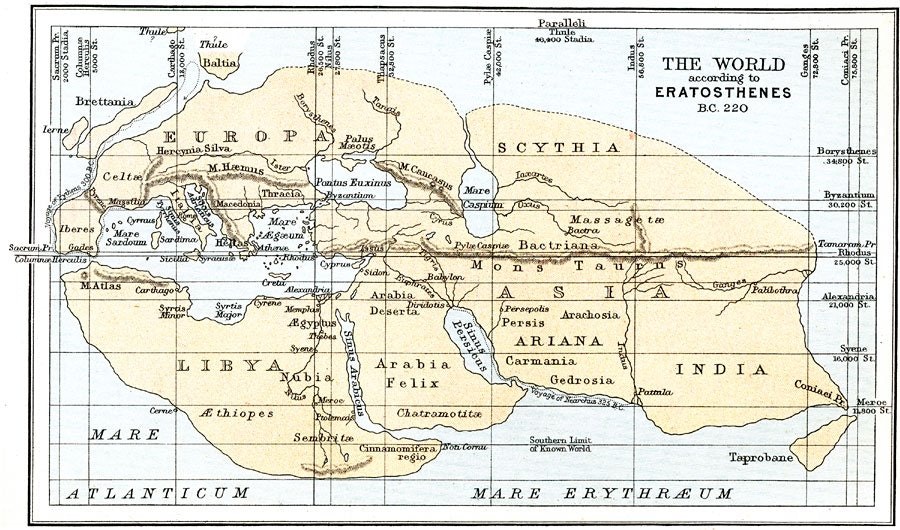
    Το 276 π.Χ. στην αποικία των Θηραίων , Κυρήνη , στην σημερινή Λιβύη γεννιέται ο Ερατοσθένης. Στα 40 του χρόνια θα γίνει βιβλιοθηκονόμος στην βιβλιοθήκη της Αλεξάνδρειας. Πρώτος απ'όλους θα καταρτίσει μια ενιαία χρονολόγηση προκειμένου να λύσει το πρόβλημα των τοπικών χρονολογήσεων που ίσχυε μέχρι τότε. Θα προσπαθήσει να διαμορφώσει την χρονολόγησή του μέχρι τον Τρωικό πόλεμο και θα καταφέρει να αποδώσει με ικανοποιητική ακρίβεια κυρίως τα έτη μετά το 312 π.Χ.

   Η πρώτη αναφορά στη σφαιρική Γη έγινε από τον Πυθαγόρα τον 6ο π.Χ. αιώνα και βασιζόταν στη αίσθηση του για την συμμετρία και την αισθητική. Αυτός που παρουσιάζει πρώτος μια δομημένη εξήγηση του γιατί η Γη είναι σφαιρική είναι ο Αριστοτέλης , περίπου 200 χρόνια αργότερα. Τα επιχειρήματά του βασίζονται στην λογική και στην παρατήρηση.

    - Κατά την σεληνιακή έκλειψη η σκιά της Γής είναι εμφανώς κυκλική.

    - Κατά την απομάκρυνση των πλοίων από το λιμάνι το κατάρτι ήταν το τελευταίο που χανόταν στον ορίζοντα.

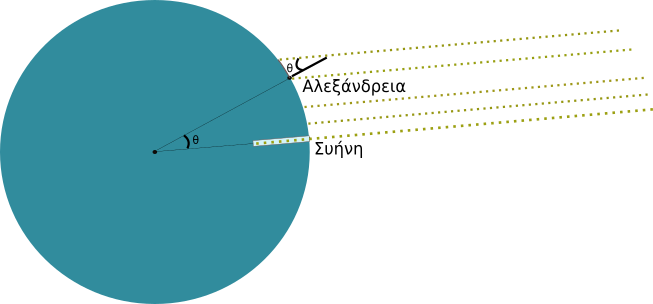
    Ο Ερατοσθένης τα γνώριζε αυτά. Ζεί περίπου 60 χρόνια μετά από την χρονιά που ο Αριστοτέλης ίδρυσε το Λύκειό του και εργαζόμενος στην βιβλιοθήκη της Αλεξάνδρειας έχει πρόσβαση σε όλη την μέχρι τότε καταγεγραμμένη ανθρώπινη γνώση. Ετσι όταν έμαθε ότι σε μια πόλη νότια της Αλεξάνδρειας που τότε λεγόταν Συήνη ( το σημερινό Ασουάν με το γνωστό φράγμα ) κατά το μεσημέρι του θερινού ηλιοστασίου ο ήλιος φώτιζε τον πάτο των πηγαδιών χωρίς να αφήνει σκιές , είχε μια καταπληκτική ιδέα. Την συγκεκριμένη μέρα και ώρα στην Αλεξάνδρεια έστησε μια ράβδο κάθετα στην Γη και μέτρησε , προφανώς με την βοήθεια της σκιάς της , την γωνία θ ανάμεσα στις ακτίνες του Ηλιου και την ράβδο. Η γωνία αυτή , με δεδομένο ότι τις ακτίνες του Ηλιου μπορούμε να τις θεωρήσουμε παράλληλες , θα έπρεπε να είναι ίση με την γωνία που αντιστοιχεί στο τόξο πάνω στην περιφέρεια της Γης ανάμεσα στην Αλεξάνδρεια και την Συήνη (οι γωνίες θ στο σχήμα είναι γωνίες εντός εναλλάξ). Υπολόγισε την γωνία θ στις 7,2 μοίρες. Αυτό που κατά πάσα πιθανότητα υπολόγισε είναι ότι η γωνία αυτή ήταν περίπου 50 φορές μικρότερη από την γωνία που αντιστοιχεί σε έναν κύκλο. Άρα με βάση τις αναλογίες και η περιφέρεια της Γης θα έπρεπε να είναι 50 φορές μεγαλύτερη απο το μήκος του τόξου ανάμεσα στις δύο πόλεις.