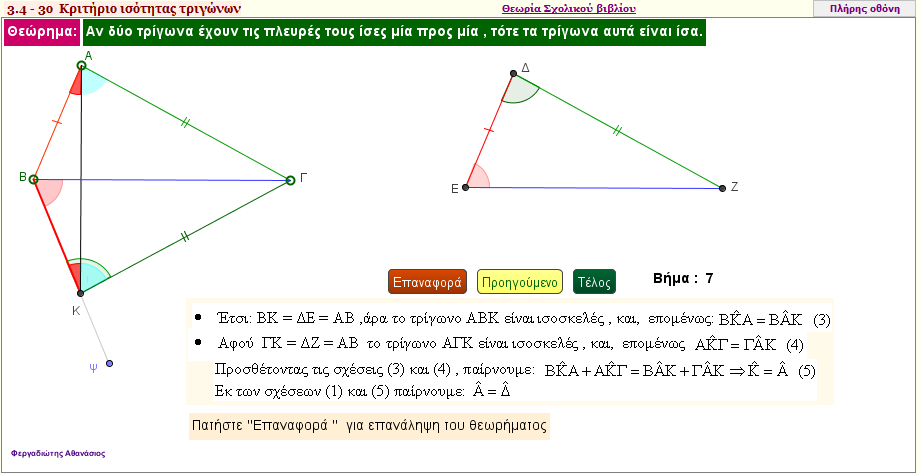
3ο Κριτήριο ισότητας τριγώνων
Αν δύο τρίγωνα έχουν τις πλευρές τους ίσες μία προς μία , τότε είναι ίσα
| | |  |
| | | | |
Ύπαρξη καθέτου από σημείο Α της ευθείας (ε) προς την (ε) - Κατασκευή 1
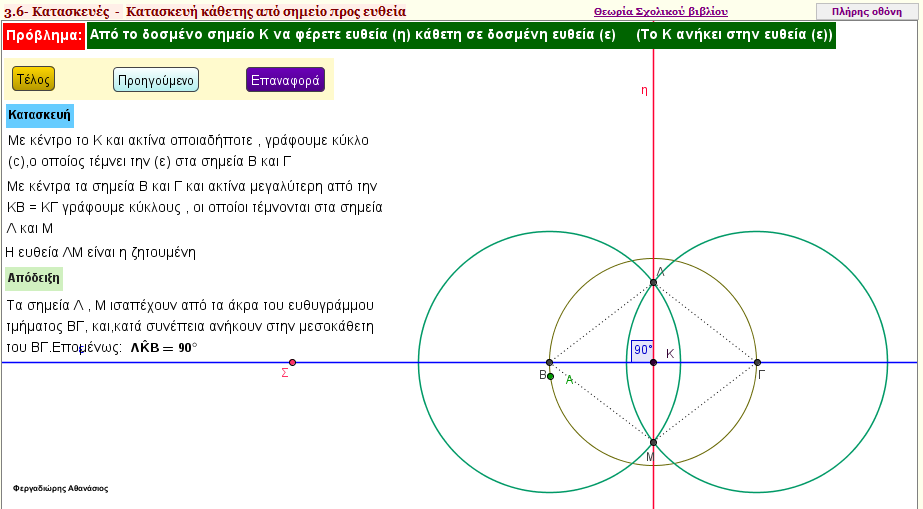
Από σημείο Κ , που βρίσκεται στην ευθεία (ε) , να χαράξετε ευθεία που να περνά από το Κ , και να είναι κάθετη στην ευθεία (ε) - Πρώτη κατασκευή
| | |  |
| | | | |
Ύπαρξη καθέτου από σημείο Α της ευθείας (ε) προς την (ε) - Κατασκευή 2
Από σημείο Κ , που βρίσκεται στην ευθεία (ε) , να χαράξετε ευθεία που να περνά από το Κ , και να είναι κάθετη στην ευθεία (ε) - Δεύτερη κατασκευή | | | 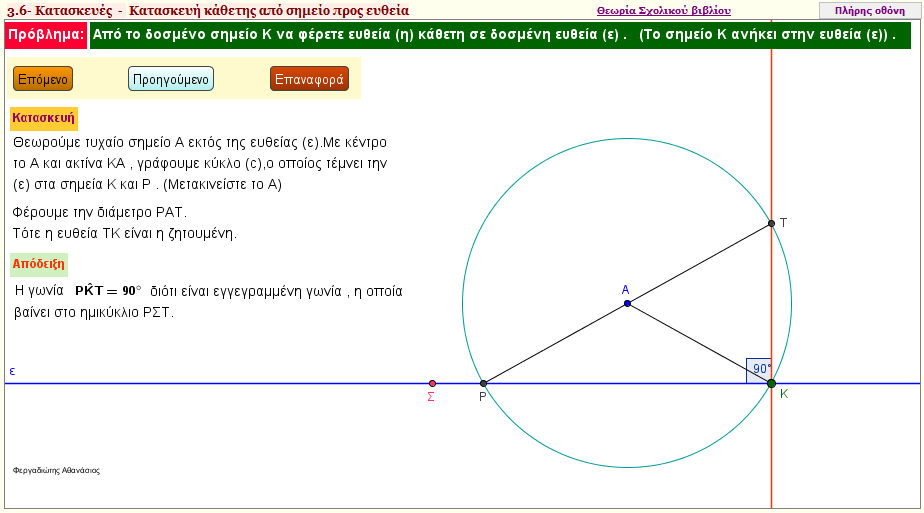 |
| | | | |
Ύπαρξη καθέτου από σημείο Α εκτός ευθείας (ε) - Κατασκευή 1
Από σημείο Κ , που βρίσκεται έξω από την ευθεία (ε) , να χαράξετε ευθεία που να περνά από το Κ , και να είναι κάθετη στην ευθεία (ε) - Πρώτη κατασκευή | | | 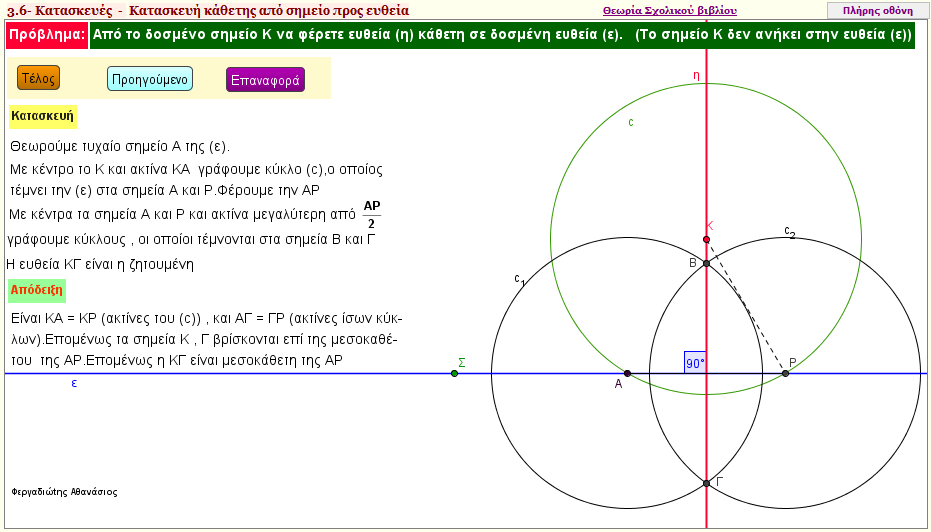 |
| | | | |
Ύπαρξη καθέτου από σημείο Α εκτός ευθείας (ε) - Κατασκευή 2
Από σημείο Κ , που βρίσκεται έξω από την ευθεία (ε) , να χαράξετε ευθεία που να περνά από το Κ , και να είναι κάθετη στην ευθεία (ε) - Δεύτερη κατασκευή | | | 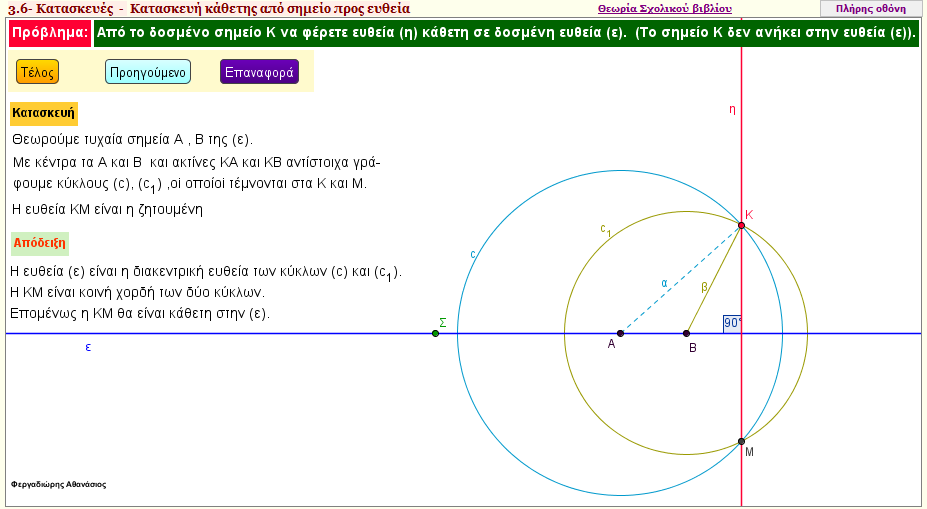 |
| | | | |
Ο Κύκλος
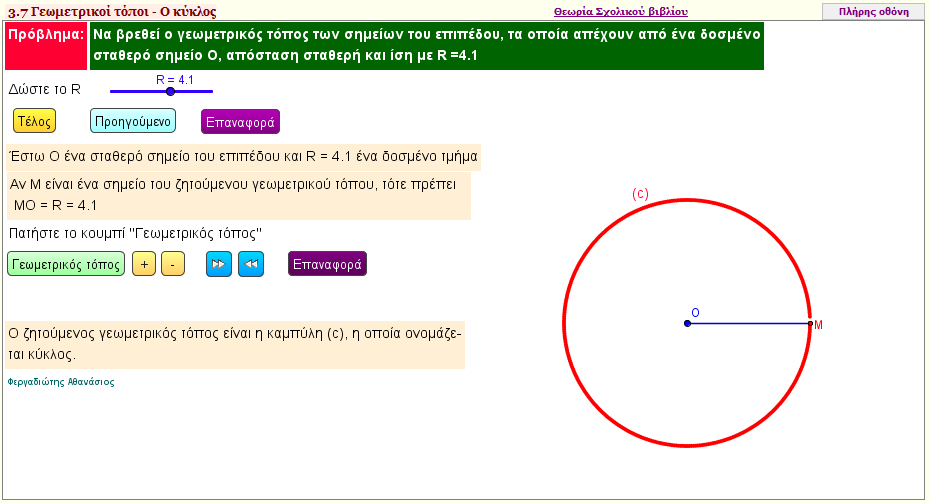
Ο κύκλος , ως γεωμετρικός τόπος σημείων του επιπέδου
Η εφαρμογή αυτή κατασκευάζει κύκλο , αφού δοθούν το κέντρο και η ακτίνα του
Μπορείτε να μετακινήσετε το κέντρο Ο του κύκλου , και να δώσετε την ακτίνα R , που θέλετε
| | |  |
| | | | |
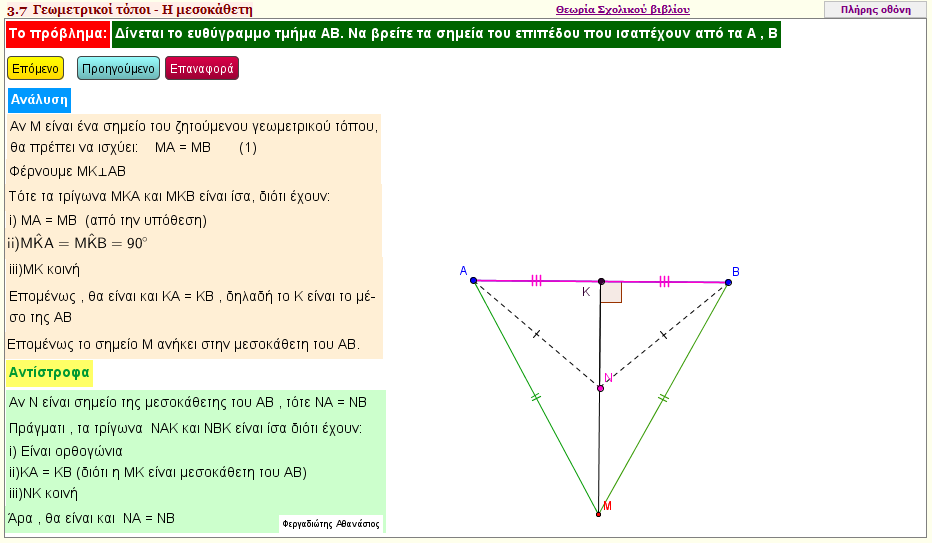
Η μεσοκάθετος ευθύγραμμου τμήματος
Η μεσοκάθετος , ως γεωμετρικός τόπος σημείων του επιπέδου
Η εφαρμογή αυτή κατασκευάζει την μεσοκάθετη , αφού δοθεί ένα ευθύγραμμο τμήμα ΑΒ
Μπορείτε να αυξομοιώσετε το μήκος του ευθυγράμμου τμήματος ΑΒ, μετακινώντας τα σημεία Α και Β
| | |  |
| | |
|
Η διχοτόμος γωνίας
Η διχοτόμος γωνίας , ως γεωμετρικός τόπος σημείων του επιπέδου
Η εφαρμογή αυτή κατασκευάζει την διχοτόμο μιας γωνίας xΟy.
Μπορείτε να δημιουργήσετε την γωνία που θέλετε , μετακινώντας την κορυφή Ο και τους οδηγούς που βρίσκονται στις πλευρές Οx , Oy της γωνίας | | | 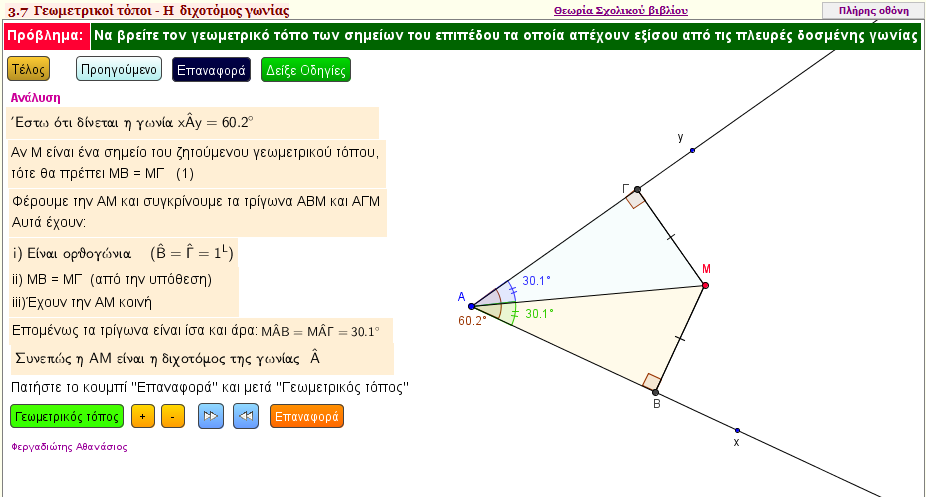 |
| | |
|
Κατασκευή διχοτόμου γωνίας
Με την εφαρμογή αυτή , κατασκευάζουμε την διχοτόμο μιας γωνίας με κανόνα και διαβήτη | | | 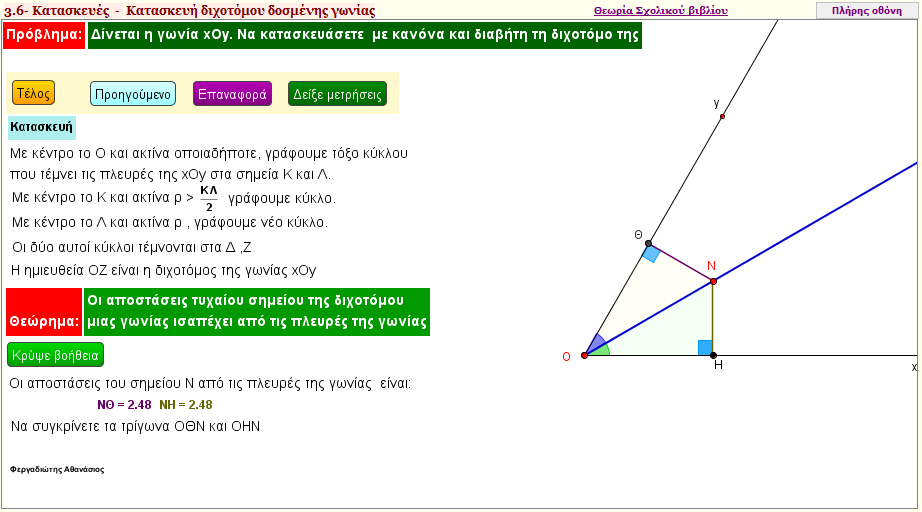 |
| | | | |
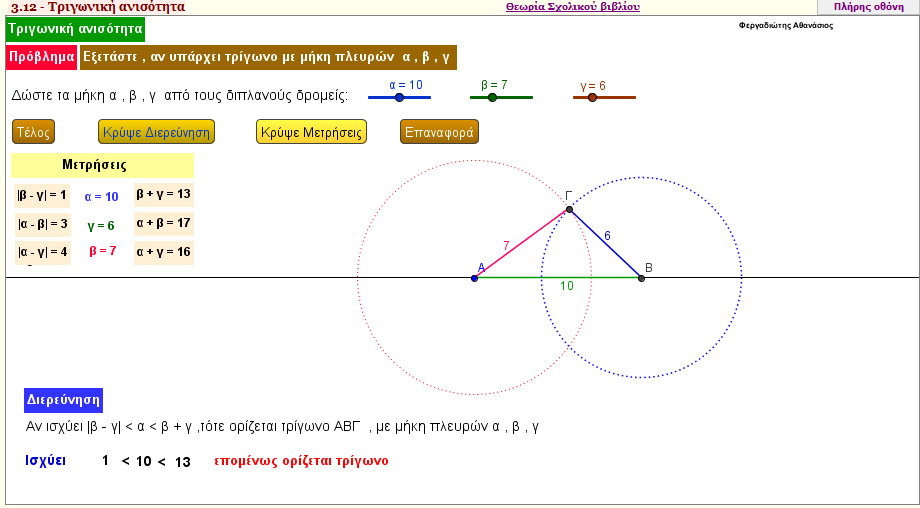
Η Τριγωνική ανισότητα
Αν σας δοθούν τα μήκη τριών ευθύγραμμων τμημάτων , πότε ορίζεται τρίγωνο με τα μήκη αυτά;
Διερευνήστε το θέμα αυτό , με την εφαρμογή αυτή.
| | |  |
| | | | |
Σχετικές θέσεις ευθείας και κύκλου
Με την εφαρμογή αυτή , εξετάστε τις σχετικές θέσεις ευθείας και κύκλου , και διατυπώστε τα συμπεράσματά σας. | | | 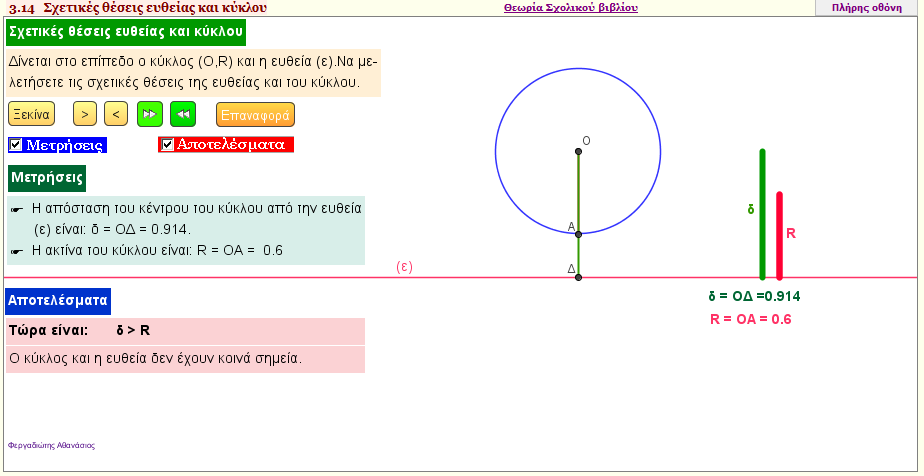 |
| | | | |
Σχετικές θέσεις δύο κύκλων
Με την εφαρμογή αυτή , εξετάστε τις σχετικές θέσεις δύο κύκλων , μελετώντας τις ακτίνες του και το μήκος της διακέντρου , και διατυπώστε τα συμπεράσματά σας. | | | 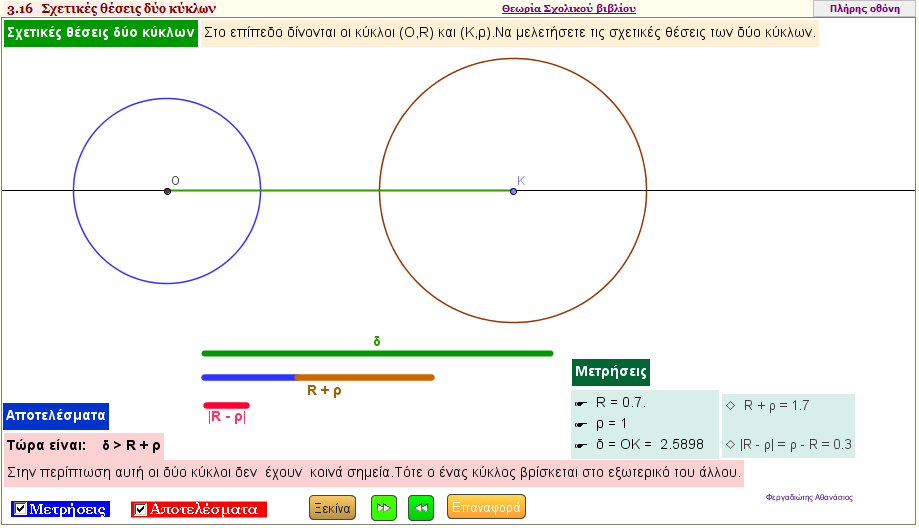 |
| | | | |
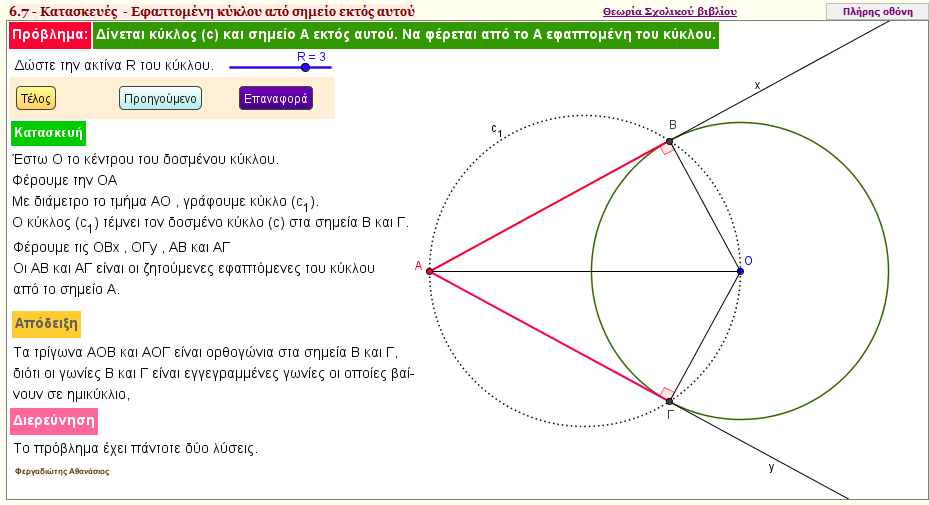
Κατασκευή εφαπτομένης από σημείο που βρίσκεται έξω από κύκλο
Με την εφαρμογή αυτή , κατασκευάζουμε την εφαπτομένη ενός κύκλου που διέρχεται από σημείο που βρίσκεται έξω από δοσμένο κύκλο
| | |  |
| | | | |
Κατασκευή τριγώνου από β =ΑΓ , γ = ΑΒ και γωνία Α
Με την εφαρμογή αυτή , κατασκευάζουμε το τρίγωνο με τα παραπάνω δοσμένα στοιχεία | | | 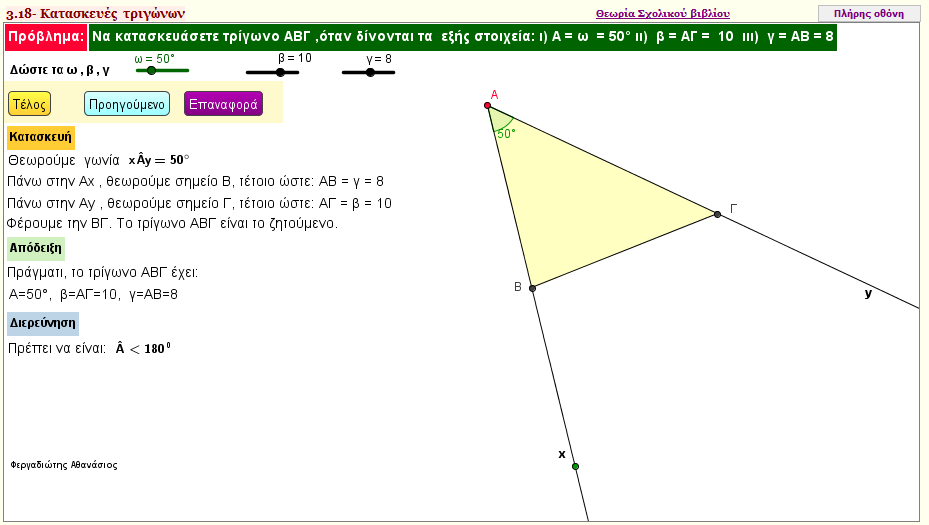 |
| | | | |
Κατασκευή τριγώνου από β =ΑΓ , γ = ΑΒ και α = ΒΓ
Με την εφαρμογή αυτή , κατασκευάζουμε το τρίγωνο με τα παραπάνω δοσμένα στοιχεία | | | 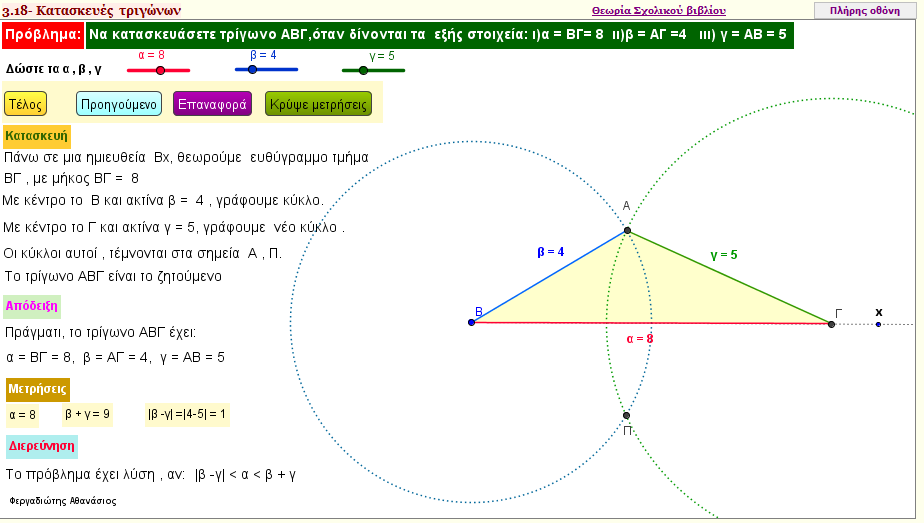 |