Αναλογίες

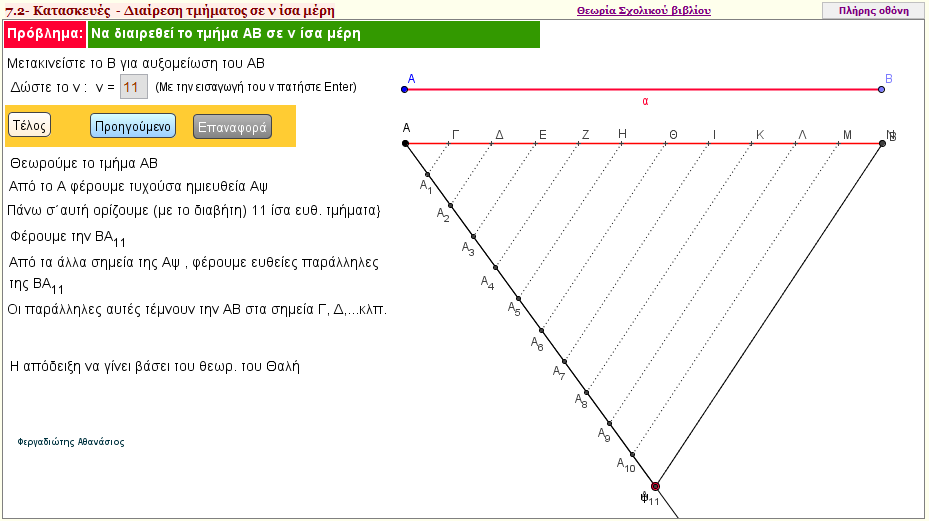
Διαίρεση ευθύγραμμου τμήματος σε ν ίσα μέρη Πως θα διαιρέσετε ένα δοσμένο ευθύγραμμο τμήμα σε ν ίσα μέρη; (Ο αριθμός ν είναι φυσικός και μεγαλύτερος του δύο)

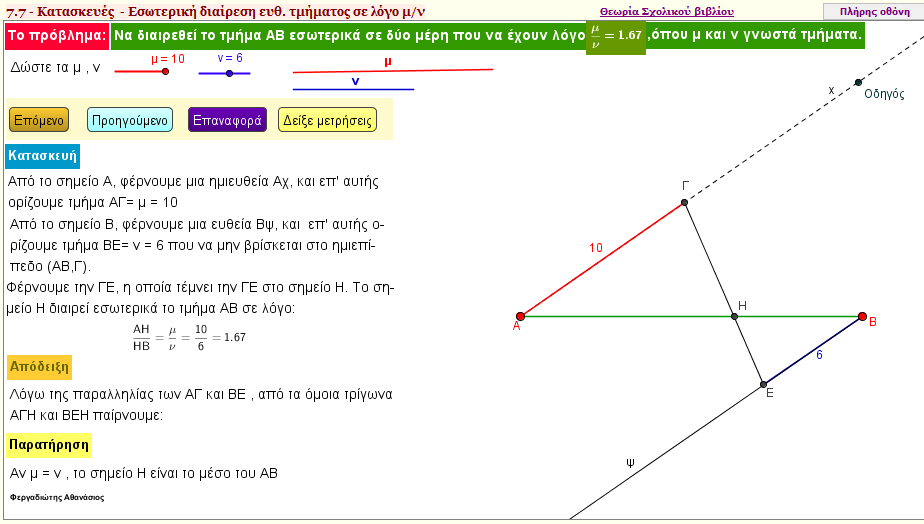
Εσωτερική διαίρεση ευθύγραμμου τμήματος Πως θα διαιρέσετε εσωτερικά ένα δοσμένο ευθύγραμμο τμήμα σε δοσμένο λόγο μ/ν; Δηλαδή , να εντοπίσετε ένα σημείο Ζ , εσωτερικό ενός δοσμένου ευθύγραμμου τμήματος ΑΒ , ώστε ο λόγος ΖΑ/ΖΒ να είναι ίσος με μ/ν

Εξωτερική διαίρεση ευθύγραμμου τμήματος Πως θα διαιρέσετε εξωτερικά ένα δοσμένο ευθύγραμμο τμήμα σε δοσμένο λόγο μ/ν; Δηλαδή , να εντοπίσετε ένα σημείο Ζ , εξωτερικό ενός δοσμένου ευθύγραμμου τμήματος ΑΒ , ώστε ο λόγος ΖΑ/ΖΒ να είναι ίσος με μ/ν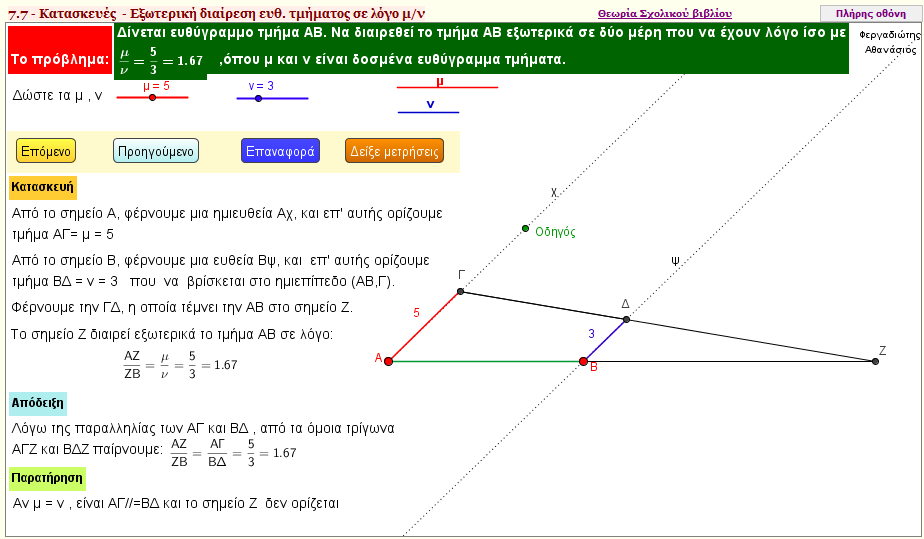

Αρμονική διαίρεση ευθύγραμμου τμήματος Πως θα διαιρέσετε εσωτερικά και εξωτερικά ένα δοσμένο ευθύγραμμο τμήμα σε δοσμένο λόγο μ/ν; Δηλαδή , να εντοπίσετε δύο σημεία Η και Ζ , Η εσωτερικό και Ζ εξωτερικό ενός δοσμένου ευθύγραμμου τμήματος ΑΒ , ώστε ο λόγος ΖΑ/ΖΒ να είναι ίσος με τον λόγο ΗΑ/ΗΒ ίσοι με μ/ν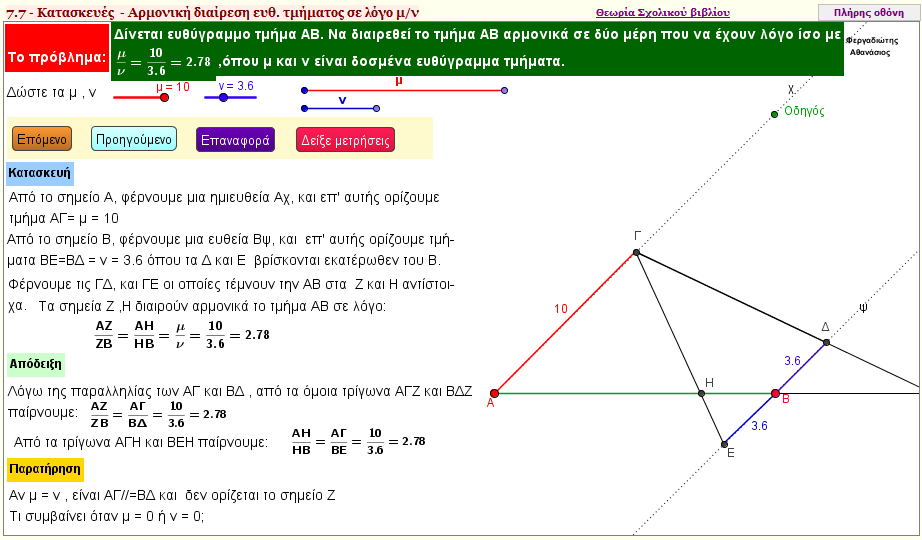

Τετάρτη ανάλογος τριών ευθύγραμμων τμημάτων 1 Όταν σας δοθούν τρία ευθύγραμμα τμήματα α , β , γ , μπορείτε να κατασκευάσετε ένα ευθύγραμμο τμήμα x , τέτοιο , ώστε α/β = γ/x; - Πρώτη απόδειξη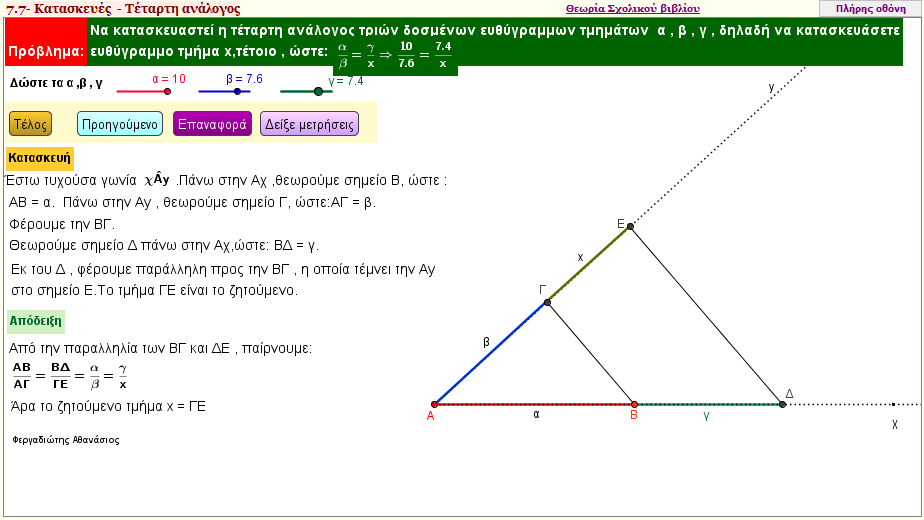

Τετάρτη ανάλογος τριών ευθύγραμμων τμημάτων 2 Όταν σας δοθούν τρία ευθύγραμμα τμήματα α , β , γ , μπορείτε να κατασκευάσετε ένα ευθύγραμμο τμήμα x , τέτοιο , ώστε α/β = γ/x; - Δεύτερη απόδειξη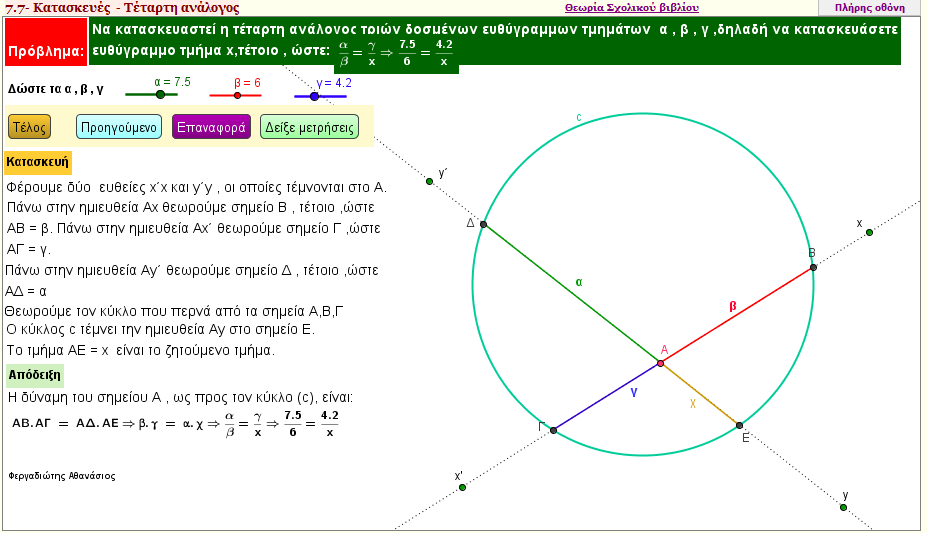

Τετάρτη ανάλογος τριών ευθύγραμμων τμημάτων 3 Όταν σας δοθούν τρία ευθύγραμμα τμήματα α , β , γ , μπορείτε να κατασκευάσετε ένα ευθύγραμμο τμήμα x , τέτοιο , ώστε α/β = γ/x; - Τρίτη απόδειξη

Συζυγή αρμονικά σημεία Όταν σας δοθεί ένα ευθύγραμμο τμήμα ΑΒ και ένα σημείο Μ εσωτερικό του ΑΒ , μπορείτε να εντοπίσετε ένα σημείο Δ εξωτερικό του ΑΒ , τέτοιο , ώστε ΜΑ/ΜΒ = ΔΑ/ΔΒ;

Ο Απολλώνιος κύκλος Ο γεωμετρικός τόπος των σημείων του επιπέδου , οι αποστάσεις των οποίων από δύο δοθέντα σημεία είναι σταθερός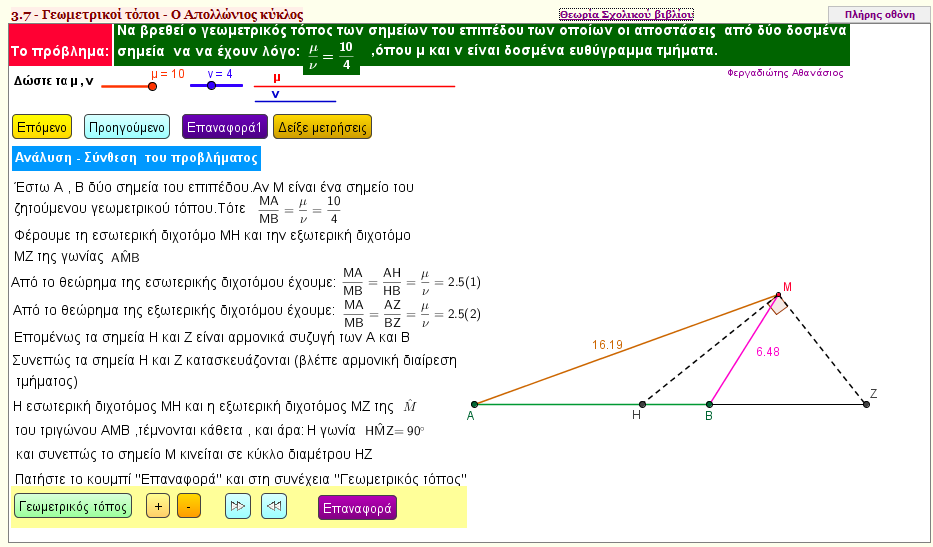