Μετρικές σχέσεις

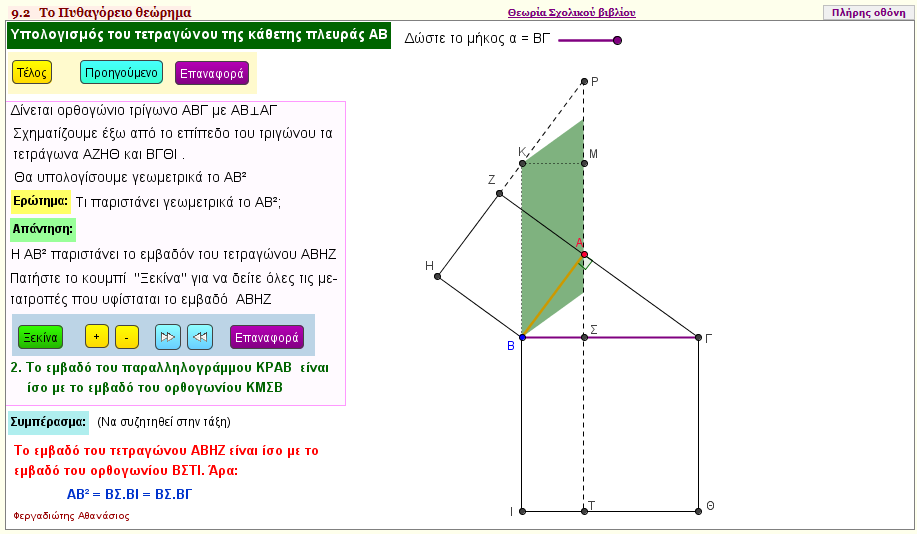
Yπολογισμός του ΑΒ² της κάθετης πλευράς ΑΒ σε ορθογώνιο τρίγωνο ΑΒΓ (1) Ποιά είναι η γεωμετρική ερμηνεία της σχέσης β² = α.ΔΒ σε ένα ορθογώνιο τρίγωνο ΑΒΓ με κάθετες πλευρές β και γ και ΔΒ είναι η προβολή της κάθετης β στην υποτείνουσα α;

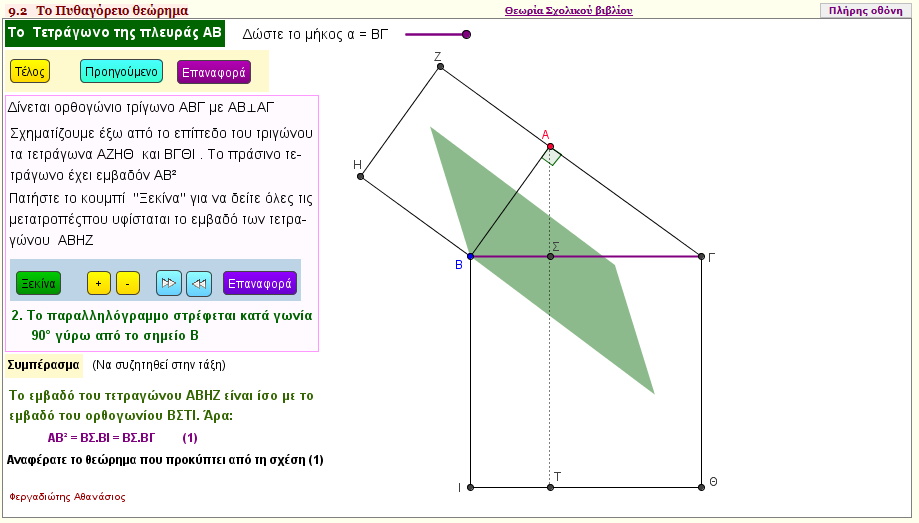
Yπολογισμός του ΑΒ² της κάθετης πλευράς ΑΒ σε ορθογώνιο τρίγωνο ΑΒΓ (2) Ποιά είναι η γεωμετρική ερμηνεία της σχέσης β² = α.ΔΒ σε ένα ορθογώνιο τρίγωνο ΑΒΓ με κάθετες πλευρές β και γ και ΔΒ είναι η προβολή της κάθετης β στην υποτείνουσα α;

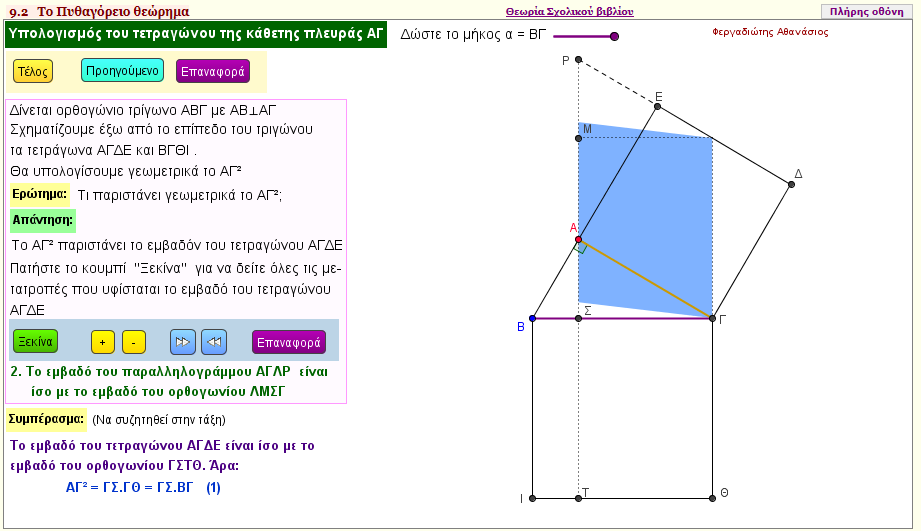
Yπολογισμός του ΑΓ² της κάθετης πλευράς ΑΓ σε ορθογώνιο τρίγωνο ΑΒΓ Ποιά είναι η γεωμετρική ερμηνεία της σχέσης γ² = α.ΔΓ σε ένα ορθογώνιο τρίγωνο ΑΒΓ με κάθετες πλευρές β και γ και ΔΓ είναι η προβολή της κάθετης γ στην υποτείνουσα α;

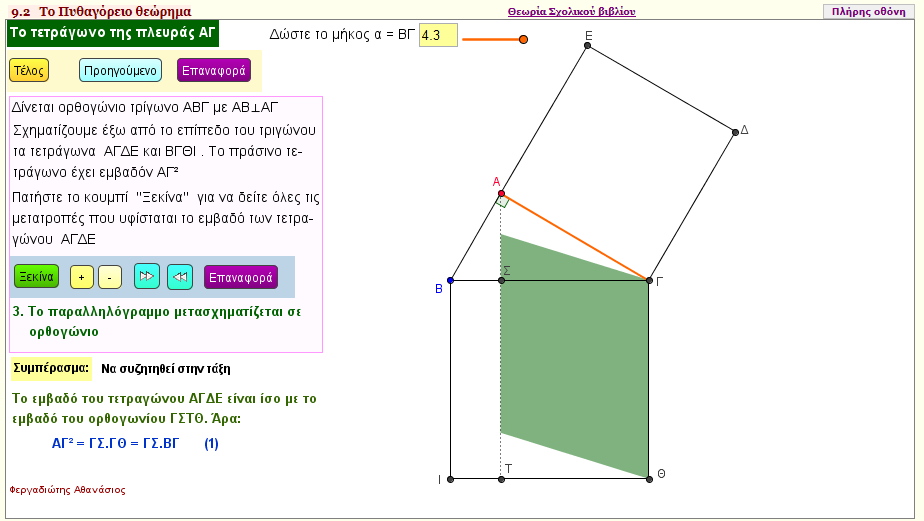
Yπολογισμός του ΑΓ² της κάθετης πλευράς ΑΓ σε ορθογώνιο τρίγωνο ΑΒΓ (2) Ποιά είναι η γεωμετρική ερμηνεία της σχέσης γ² = α.ΔΓ σε ένα ορθογώνιο τρίγωνο ΑΒΓ με κάθετες πλευρές β και γ και ΔΓ είναι η προβολή της κάθετης γ στην υποτείνουσα α;

Το Πυθαγόρειο Θεώρημα 1 Μια απόδειξη του Πυθαγορείου θεωρήματος

Το Πυθαγόρειο Θεώρημα 2 Μια απόδειξη του Πυθαγορείου θεωρήματος

Το Πυθαγόρειο Θεώρημα 3 Μια απόδειξη του Πυθαγορείου θεωρήματος

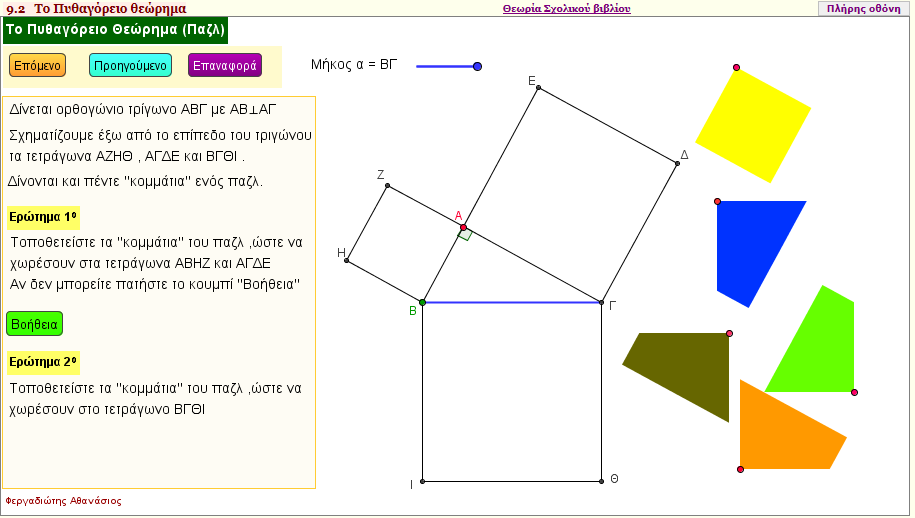
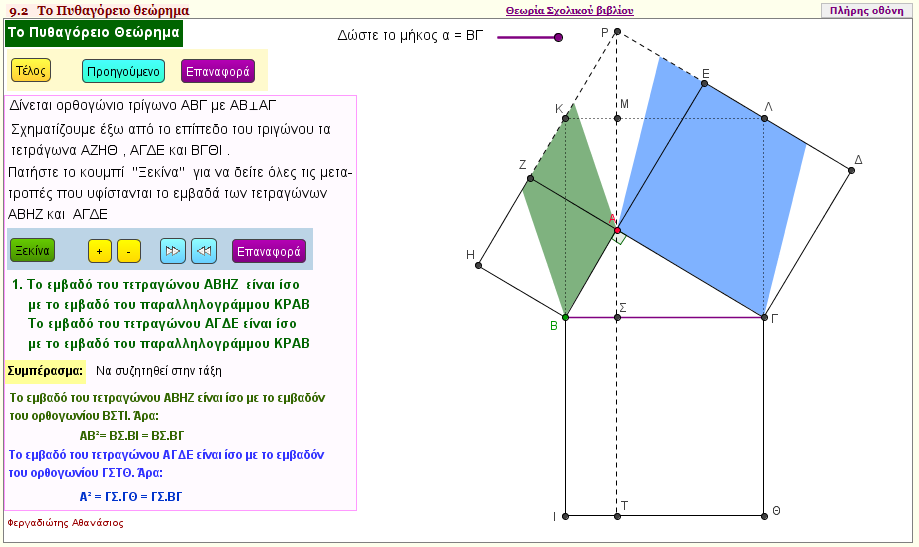
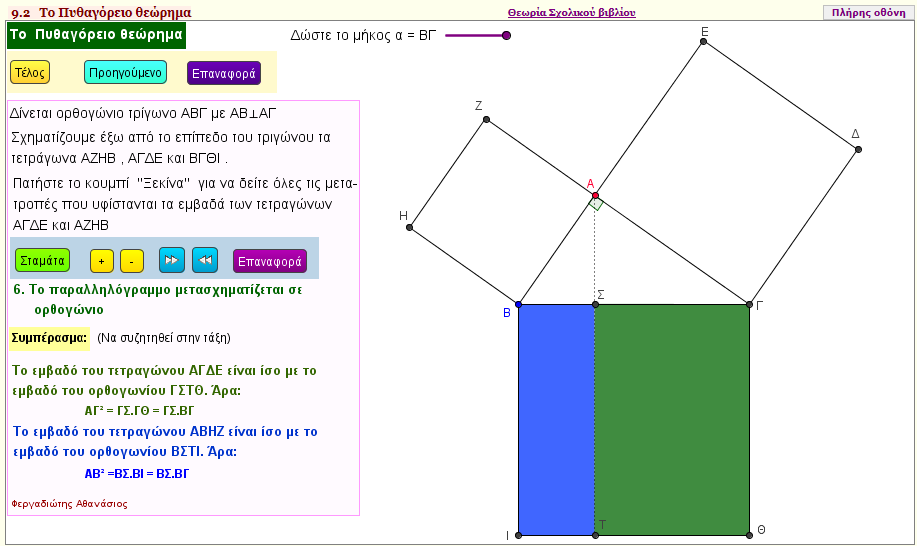
Το Πυθαγόρειο θεώρημα (παζλ) 4 Με την εφαρμογή αυτή αποδεικνύουμε το Πυθαγόρειο θεώρημα , τοποθετώντας τα κομμάτια του ''παζλ'' στα τετράγωνα που δημιουργούνται με τις πλευρές του ορθογώνιου τριγώνου ΑΒΓ εκτός του επιπέδου του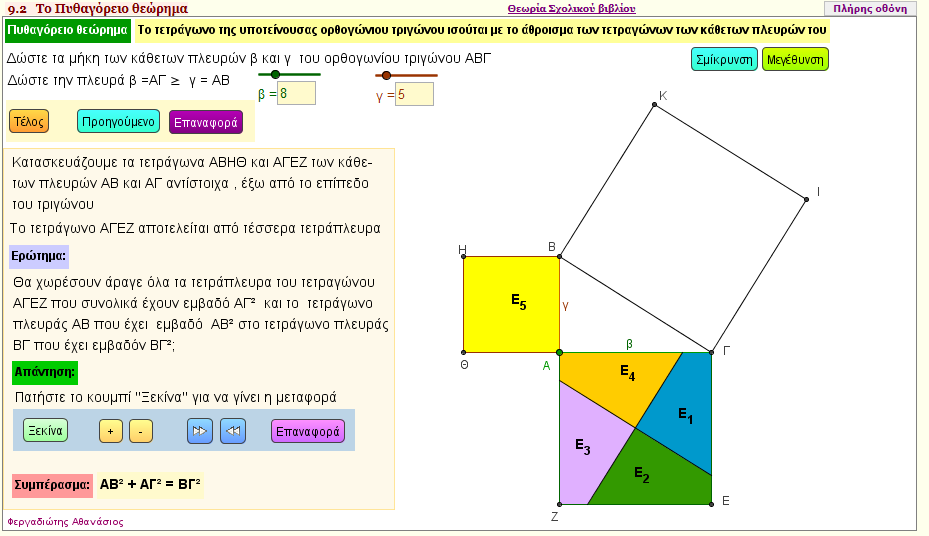

Το Πυθαγόρειο θεώρημα (παζλ) 5 Με την εφαρμογή αυτή αποδεικνύουμε το Πυθαγόρειο θεώρημα , τοποθετώντας τρίγωνα με κέθετες πλευρές β και γ και υποτείνουσα α σε ένα τετράγωνο με πλευρά α + β.

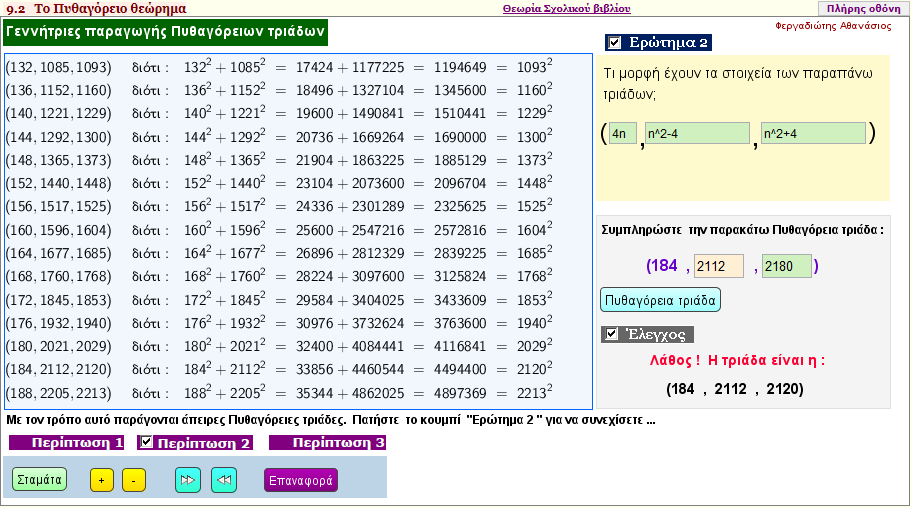
Γεννήτρια Πυθαγόρειων τριάδων Με την βοήθεια της εφαρμογής αυτής δημιουργούμε Πυθαγόρειες τριάδες , δηλαδή τριάδες της μορφής (α , β , γ) για τις οποίες ισχύει το Πυθαγόρειο θεώρημα. Προσπαθείστε , κατόπιν τριών περιπτώσεων παραγωγής Πυθαγόρειων τριάδων , να εντοπίσετε τον γενικό τύπο παραγωγής των Πυθαγόρειων τριάδων με βάση την εφαρμογή αυτή.


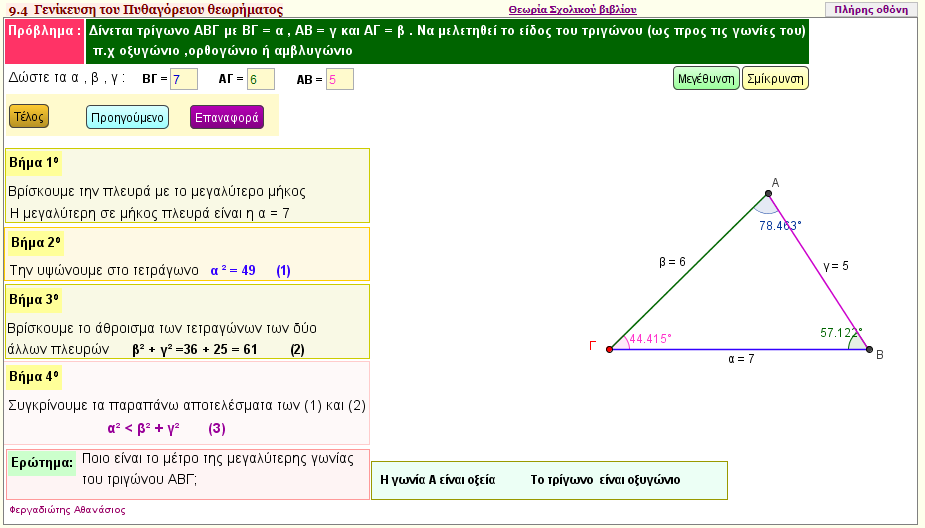
Μελέτη του είδους του τριγώνου , ως προς τις γωνίες του Δώστε τις πλευρές α = ΒΓ , β = ΑΓ και γ = ΑΒ για να μελετηθούν τα παρακάτω α) Αν τα παραπάνω δοσμένα μήκη αποτελούν πλευρές τριγώνου β)Να εξεταστεί αν το τρίγωνο είναι οξυγώνιο , αμβλυγώνιο ή ορθογώνιο

Υπολογισμός όλων των προβλών των πλευρών σε τυχαίο τρίγωνο Δώστε τις πλευρές α = ΒΓ , β = ΑΓ και γ = ΑΒ για να βρείτε: α) Αν τα παραπάνω δοσμένα μήκη αποτελούν πλευρές τριγώνου β)Τα μήκη όλων των προβολών των πλευρών του τριγώνου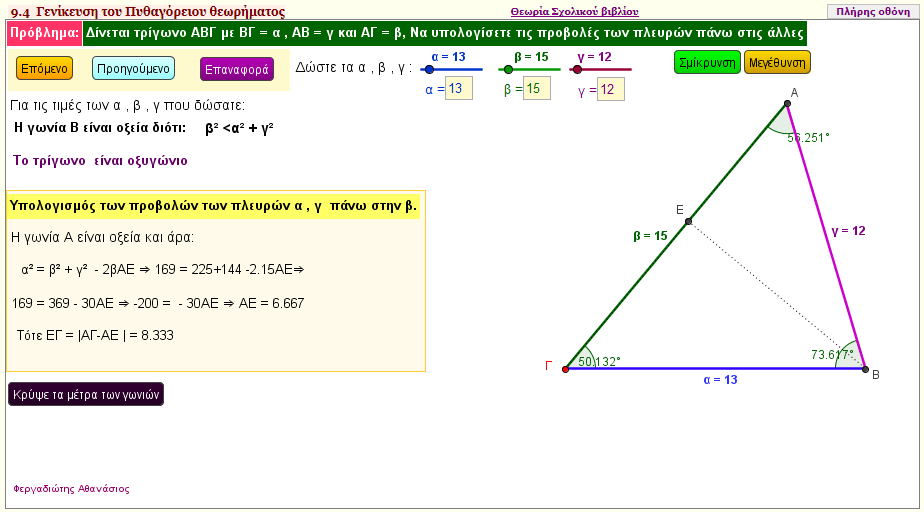

Υπολογισμός του μήκους όλων των διαμέσων σε τυχαίο τρίγωνο Δώστε τις πλευρές α = ΒΓ , β = ΑΓ και γ = ΑΒ για να βρείτε: α) Αν τα παραπάνω δοσμένα μήκη αποτελούν πλευρές τριγώνου β)Τα μήκη όλων των διαμέσων του τριγώνου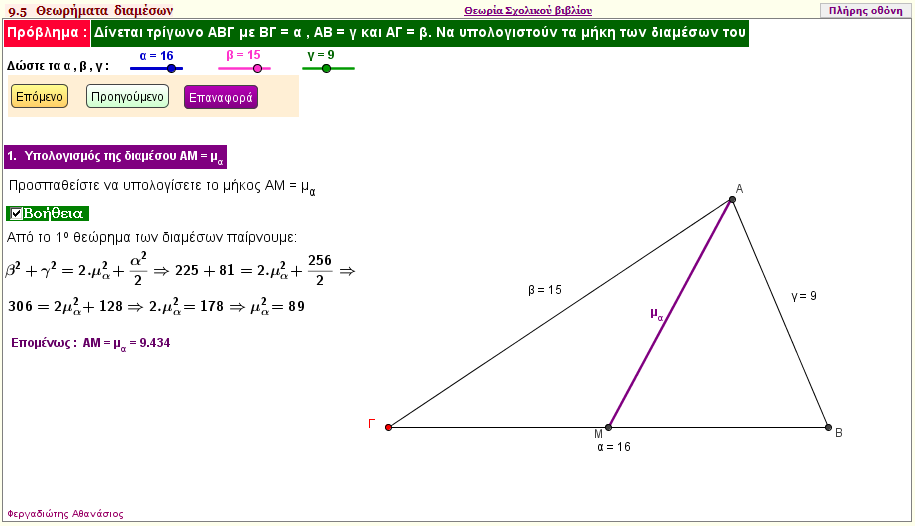

Υπολογισμός του μήκους των προβλών των διαμέσων σε τυχαίο τρίγωνο Δώστε τις πλευρές α = ΒΓ , β = ΑΓ και γ = ΑΒ για να βρείτε: α) Αν τα παραπάνω δοσμένα μήκη αποτελούν πλευρές τριγώνου β)Τα μήκη όλων των προβολών των διαμέσων του τριγώνου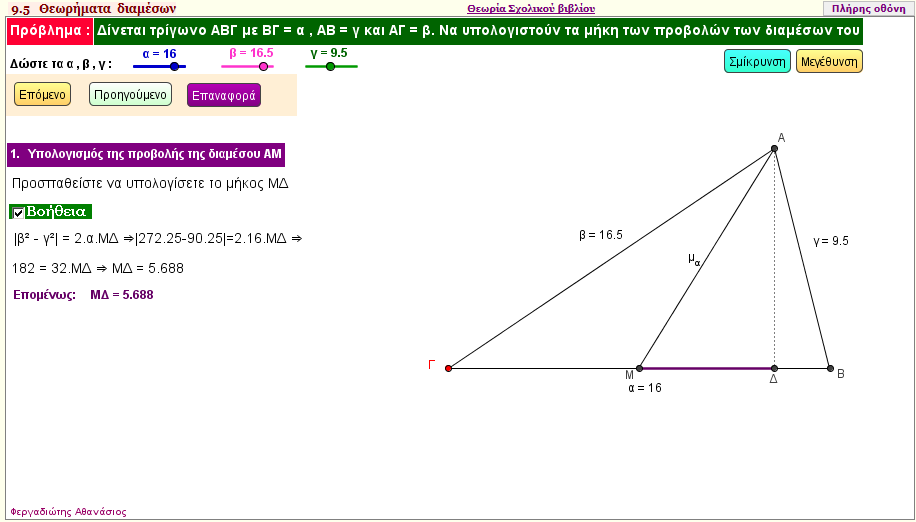
Προβλήματα γεωμετρικών τόπων
Πρόβλημα 1 Δίνονται δύο σταθερά σημεία Α και Β και ένα ευθύγραμμο τμήμα k. Nα βρείτε τον γεωμετρικό τόπο των σημείων, των οποίων το άθροισμα των τετραγώνων των αποστάσεων από τα Α , Β ισούται με k².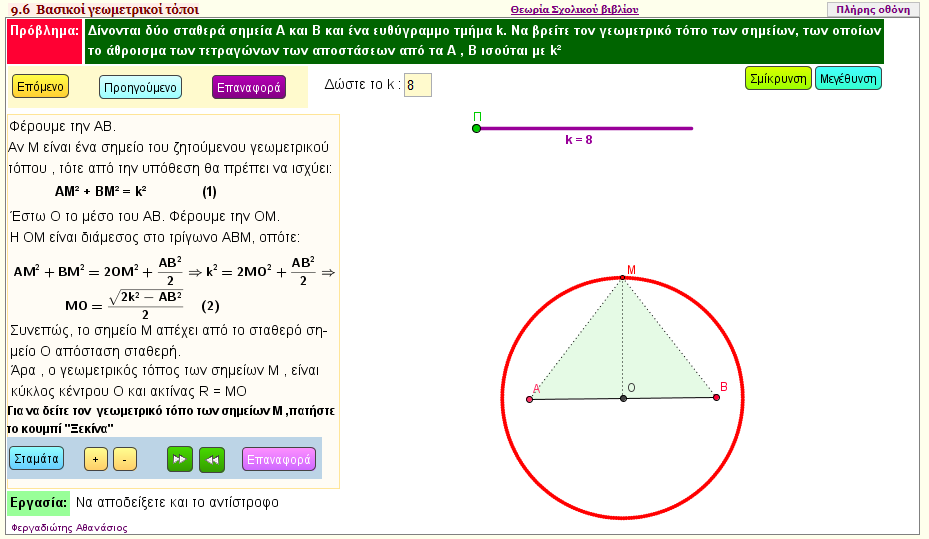

Πρόβλημα 2 Δίνονται δύο σταθερά σημεία Α και Β και ένα ευθύγραμμο τμήμα k. Nα βρείτε τον γεωμετρικό τόπο των σημείων, για τα οποία η διαφορά των τετραγώνων των αποστάσεών τους από τα Α , Β ισούται με k²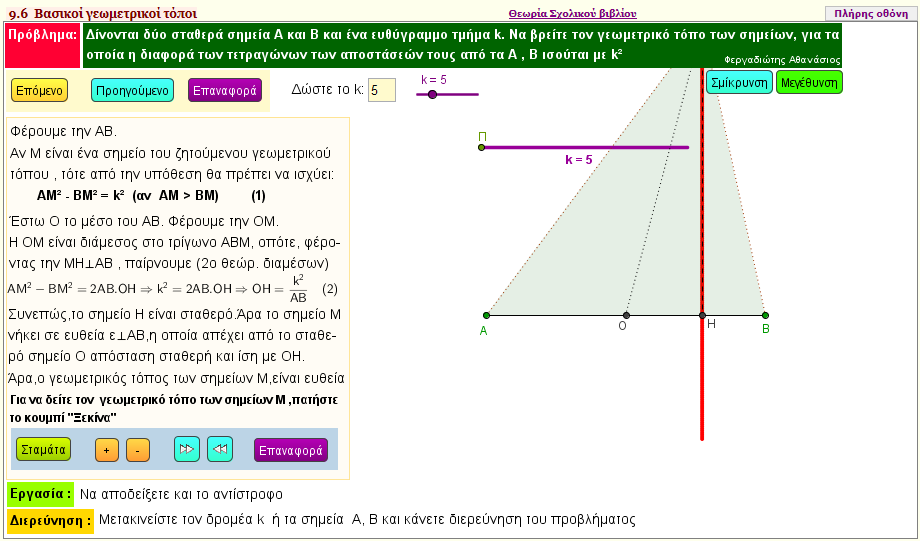
Bασικό Θεώρημα
Θεώρημα του Stewart Έστω τρίγωνο ΑΒΓ με ΑΒ = γ , ΑΓ = β και ΒΓ = α. Έστω Δ τυχαίο σημείο της ΒΓ. Θέτουμε ΒΔ = λ , ΓΔ = μ και ΑΔ = δ. Να αποδείξετε τη μετρική σχέση:μβ²+λγ² = α(δ²+ λμ)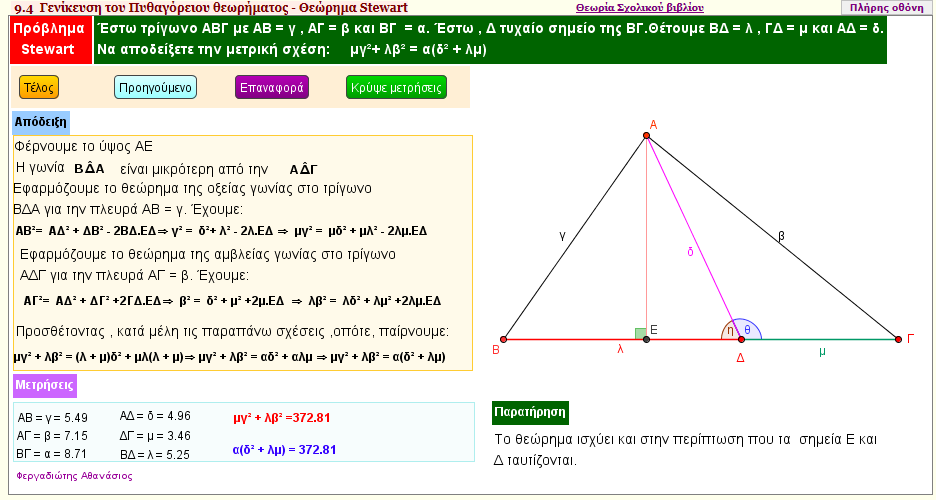
Δύναμη σημείου ως προς κύκλο - Τέμνουσες κύκλου
Δύναμη σημείου ως προς κύκλο - Θεωρία Τι παριστάνει η δύναμη ενος σημείου Ρ ως προς ένα κύκλο (Ο,ρ) για τις διάφορες θέσεις του σημείου Ρ;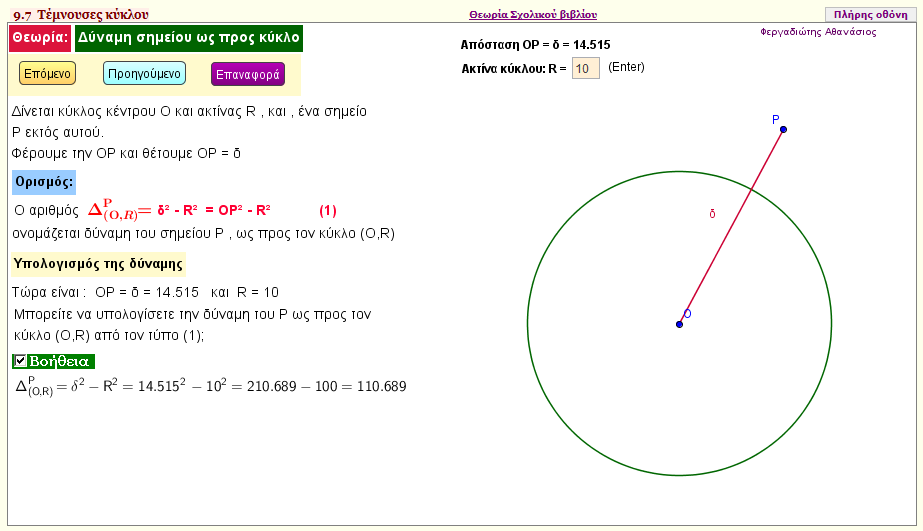

Τέμνουσες κύκλου Αν σας δοθεί ένας κύκλος (Ο,ρ) και δύο χορδές ΑΒ και ΓΔ αυτού , οι οποίες τέμνονται στο Ρ, τότε διαπιστώστε με βάση την εφαρμογή αυτή ότι ΡΑ.ΡΒ = ΡΓ.ΡΔ = R² - δ² , μετακινώντας τα σημεία Α , Β , Γ , Δ πάνω στον κύκλο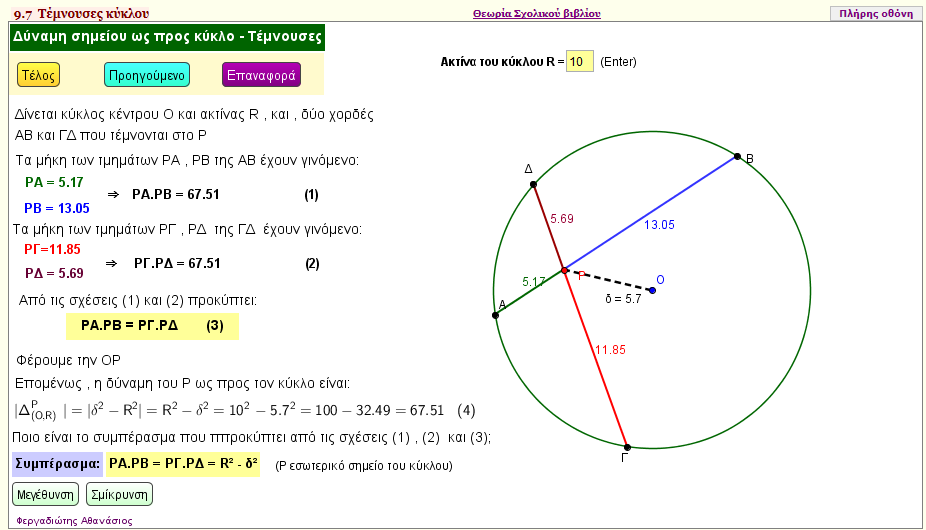

Τέμνουσες κύκλου - Γενική περίπτωση Αν σας δοθεί ένας κύκλος (Ο,ρ) και δύο χορδές ΑΒ και ΓΔ αυτού , οι οποίες τέμνονται στο Ρ (είτε στο εσωτερικό είτε στο εξωτερικό μέρος του κύκλου), τότε διαπιστώστε με βάση την εφαρμογή αυτή ότι ΡΑ.ΡΒ = ΡΓ.ΡΔ = \|δ² - R²\| = ΡΣ² (ΡΣ εφαπτομένη του κύκλου από το σημείο Ρ) μετακινώντας τα σημεία Α , Β , Γ , Δ πάνω στον κύκλο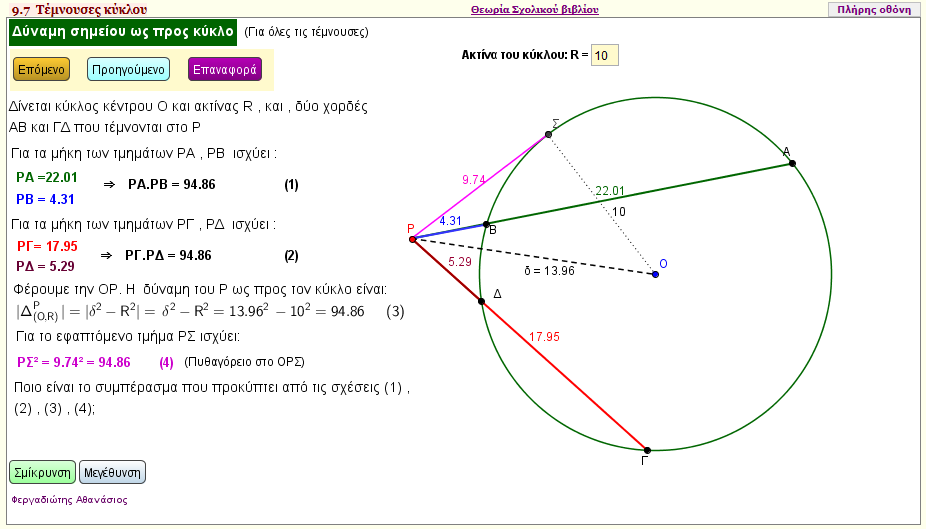

Το πρόβλημα της Χρυσής τομής Να διαιρεθεί ένα δοσμένο τμήμα ΑΒ = α σε δύο άνισα τμήματα ΑΓ ,ΓΒ ,ώστε , το μεγαλύτερο από αυτά τα τμήματα να είναι μέσο ανάλογο του μικροτέρου και του αρχικού τμήματος ΑΒ Δηλαδή, αν ΑΓ είναι το μεγαλύτερο τμήμα , να ισχύει: ΑΓ² = ΑΒ.ΓΒ Διαίρεση ενός ευθύγραμμου τμήματος σε μέσο και άκρο λόγο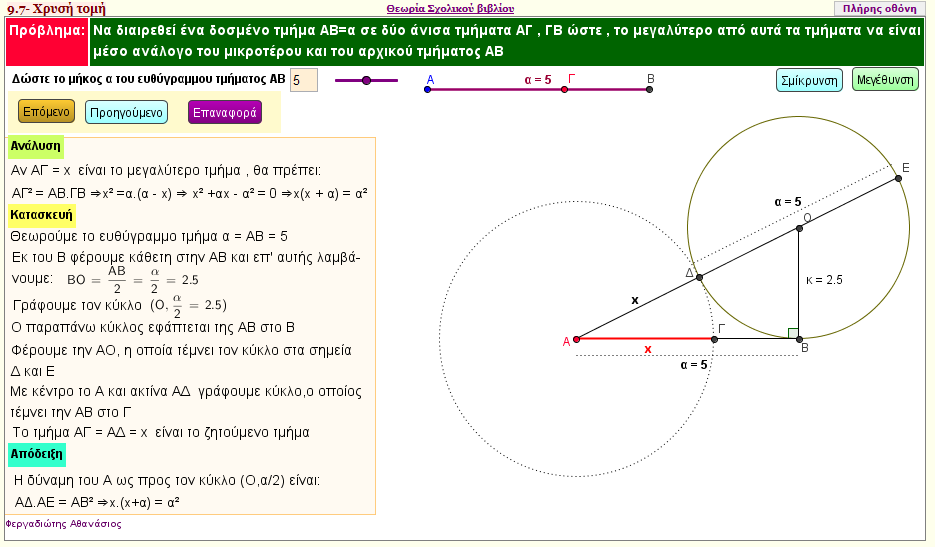

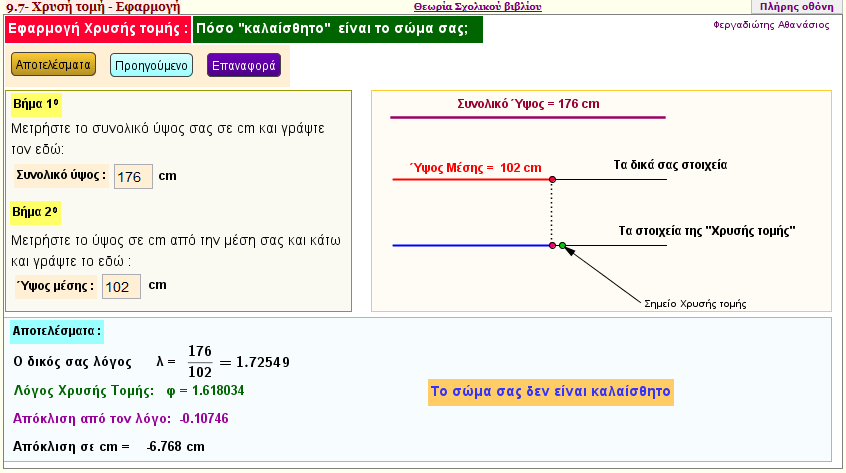
Χρυσή τομή - Εφαρμογή Ο Έλληνας γλύπτης Φειδίας , χρησιμοποιούσε τον αριθμό φ = 1,618034 για να έχουν τα γλυπτά του την αίσθηση της αρμονίας. Το ίδιο έκαναν οι αρχαίοι Έλληνες στην κατασκευή του Παρθενώνα. Είναι το δικό σας σώμα ''καλαίσθητο''; 1. Μετρήστε το α = συνολικό ύψος σας και β =το ύψος της μέσης σας 2. Βρείτε το πηλίκο α/β Αν -0.03 < α/β < 0.03 το σώμα σας έχει την αίσθηση της αρμονίας

Ριζικός άξονας δύο κύκλων Δίνονται δύο κύκλοι.Ζητάμε να βρούμε τα σημεία του επιπέδου που έχουν ίσες δυνάμεις ως προς τους δύο κύκλους.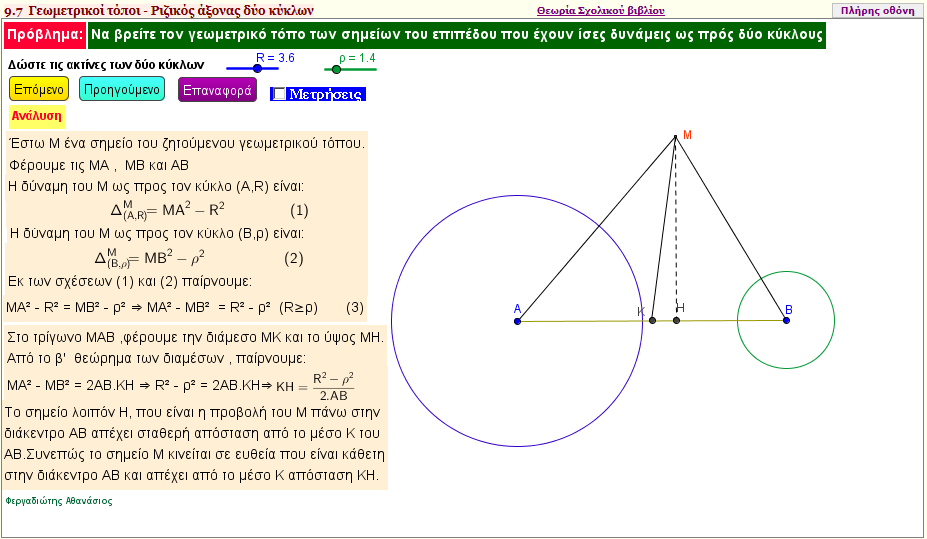

Κατασκευή τέταρτης αναλόγου 1 Κατασκευή ενός τμήματος x , τέτοιο, ώστε α/β = γ/x , όπου α , β , γ είναι γνωστά ευθύγραμμα τμήματα.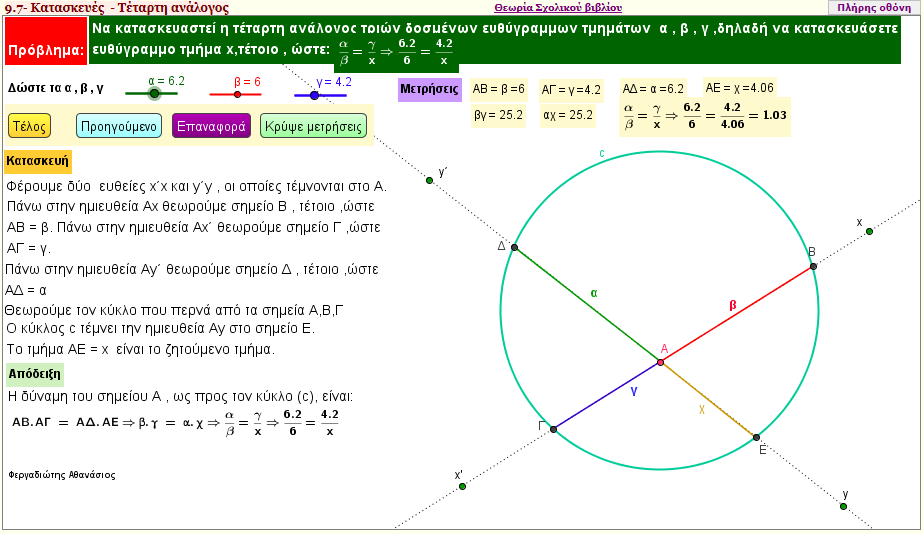

Κατασκευή τέταρτης αναλόγου 2 Κατασκευή ενός τμήματος x , τέτοιο, ώστε α/β = γ/x , όπου α , β , γ είναι γνωστά ευθύγραμμα τμήματα.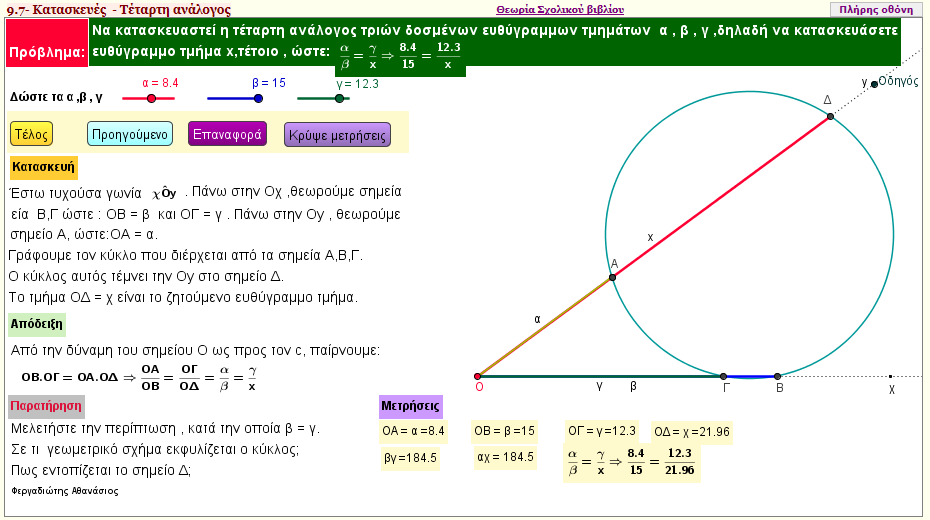