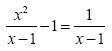3.1Εξισώσεις 1oυ βαθμού

Η Εξίσωση αx + β = 0

Στο Γυμνάσιο μάθαμε τον τρόπο επίλυσης των εξισώσεων της μορφής αx + β = 0 για συγκεκριμέ–νους αριθμούς α, β, με α ≠ 0.
Γενικότερα τώρα, θα δούμε πώς με την βοήθεια των ιδιοτήτων των πράξεων, επιλύουμε την παραπάνω εξίσωση, οποιοιδήποτε και αν είναι οι αριθμοί α, β .

Έχουμε λοιπόν

αx + β = 0 <=> αx + β – β = – β
<=> αx = –β

Διακρίνουμε τώρα τις περιπτώσεις:

Αν α ≠ 0 τότε:

αx = –β <=>

Επομένως, αν α ≠ 0 η εξίσωση έχει ακριβώς μία λύση, την .

Αν α = 0 , τότε η εξίσωση αx = – β γίνεται 0x = –β, η οποία:

αν είναι β ≠ 0 δεν έχει λύση και γι αυτό λέμε ότι είναι αδύνατη, ενώ
αν είναι β = 0 έχει τη μορφή 0x = 0 και αληθεύει για κάθε πραγματικό αριθμό x δηλαδή είναι ταυτότητα.

Η λύση της εξίσωσης αx + β = 0 και γενικά κάθε εξίσωσης λέγεται και ρίζα αυτής.

Για παράδειγμα

Για την εξίσωση 4(x – 5) = x – 5 έχουμε:

4(x – 5) = x – 5 <=> 4x – 20 = x – 5
<=> 4x – x = 20 – 5
<=> 3x = 15
<=>=5.

Άρα, η εξίσωση έχει μοναδική λύση, την x = 5 .

Για την εξίσωση 3x – x – 3 = 2x Έχουμε

3x – x – 3 = 2x <=> 3x – x – 2x = 3 <=> 0x = 3

Για τη εξίσωση 4(x – 5) – x = 3x – 20 έχουμε

4x – 20 – x = 3x – 20 <=> 4x – x – 3x = 20 – 20 <=> 0x = 0

που είναι ταυτότητα.

ΣΧΟΛΙΟ

Όπως βλέπουμε στα παραπάνω παραδείγματα, κάθε φορά καταλήγουμε σε εξίσωση της μορφής αx + β = 0, της οποίας οι συντελεστές α και β είναι συγκεκριμένοι αριθμοί και μπορούμε αμέσως να δούμε ποια από τις προηγούμενες περιπτώσεις ισχύει. Δεν συμβαίνει όμως το ίδιο, αν οι συντελεστές α και β της εξίσωσης αx + β = 0 εκφράζονται με τη βοήθεια γραμμάτων. Σε τέτοιες περιπτώσεις, τα γράμματα αυτά λέγονται παράμετροι, η εξίσωση λέγεται παραμετρική και η εργασία που κάνουμε για την εύρεση του πλήθους των ριζών της λέγεται διερεύνηση.

Για παράδειγμα η εξίσωση

(λ² – 1)x – λ + 1 = 0, λ R

έχει παράμετρο το λ και γράφεται ισοδύναμα

(λ² – 1)x – λ + 1 = 0 <=> (λ² – 1)x = λ – 1
<=> (λ + 1)(λ – 1)x = λ – 1

Επομένως

Αν λ ≠ –1 και λ ≠ 1, η εξίσωση έχει μοναδική λύση, την

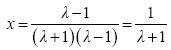
Αν λ = –1, η εξίσωση γίνεται 0x = –2 και είναι αδύνατη.

Αν λ = 1, η εξίσωση γίνεται 0x = 0 και είναι ταυτότητα.

ΕΦΑΡΜΟΓΗ

Ένας ποδηλάτης πήγε από μια πόλη Α σε μία πόλη Β και επέστρεψε από τον ίδιο δρόμο. Στην μετάβαση οδηγούσε με μέση ταχύτητα 25km/h και ξεκουράστηκε ενδιάμεσα 1 ώρα. Στην επιστροφή οδηγούσε με μέση ταχύτητα 20 km/h και δεν έκανε καμία στάση. Αν ο συνολικός χρόνος του ταξιδιού ήταν 10 ώρες, να υπολογιστεί το μήκος της διαδρομής ΑΒ.

ΛΥΣΗ

Αν x km είναι η απόσταση ΑΒ, τότε ο ποδηλάτης χρειάστηκε ώρες για να πάει από το Α στο Β και ώρες για να επιστρέψει. Αφού ξεκουράστηκε και 1 ώρα, ο συνολικός χρόνος του ταξιδιού ήταν

Επειδή ο χρόνος αυτός είναι 10 ώρες έχουμε την εξίσωση:

=10

Λύνουμε την εξίσωση και έχουμε:

=10 <=> 4x + 5x + 100 = 1000
<=> 9x = 900
<=> x = 100

Άρα το μήκος της διαδρομής είναι 100 km.

Εξισώσεις που ανάγονται σε εξισώσεις 1ου βαθμού

Στην συνέχεια θα δούμε, με τη βοήθεια παραδειγμάτων, πώς μπορούμε να επιλύσουμε εξισώσεις οι οποίες δεν είναι μεν εξισώσεις 1ου βαθμού, αλλά, με κατάλληλη διαδικασία, ανάγονται σε εξισώσεις 1ου βαθμού.

ΠΑΡΑΔΕΙΓΜΑ 1ο

Να λυθεί η εξίσωση

ΛΥΣΗ

Η εξίσωση αυτή ορίζεται για κάθε x ≠ 1. Με αυτόν τον περιορισμό έχουμε:

Επομένως η εξίσωση έχει μοναδική λύση, την x = 0.

ΠΑΡΑΔΕΙΓΜΑ 2_ο

Να λυθεί η εξίσωση

|2x –1| = |x + 3|

ΛΥΣΗ

Από τις ιδιότητες των απολύτων τιμών έχουμε:

|2x –1| = |x + 3| <=> 2x – 1 = x + 3 ή 2x –1 = –(x + 3)

Όμως:

2x – 1 = x + 3 <=> 2x – x = 4 <=> x = 4

2x – 1 = –(x + 3) <=> 2x + x = –3 + 1 <=> 3x = –2 <=> .

Επομένως η εξίσωση έχει δυο λύσεις, τους αριθμούς 4 και .

ΣΧΟΛΙΟ

Με τον ίδιο τρόπο λύνουμε κάθε εξίσωση της μορφής |f(x)| = |g(x)| .

ΠΑΡΑΔΕΙΓΜΑ 3_ο

Να λυθεί η εξίσωση

|2x – 3| = 3x – 2

ΛΥΣΗ

Επειδή το πρώτο μέλος της εξίσωσης είναι μη αρνητικό, για να έχει λύση η εξίσωση αυτή πρέπει και το δεύτερο μέλος της να είναι μη αρνητικό. Δηλαδή, πρέπει:

3x – 2 > 0 (1)

Με αυτόν τον περιορισμό, λόγω των ιδιοτήτων των απόλυτων τιμών, έχουμε:

|2x – 3| = 3x – 2<=> 2x – 3 = 3x – 2 ή 2x – 3 = 2 – 3x

<=> 2x – 3x = –2 + 3 ή 2x + 3x = 2 + 3

<=> –x = 1 ή 5x = 5

<=> x = –1 ή x = 1

Από τις παραπάνω λύσεις δεκτή είναι μόνο η x = 1, διότι μόνο αυτή ικανοποιεί τον περιορισμό (1).

ΣΧΟΛΙΟ

Με τον ίδιο τρόπο λύνουμε εξισώσεις της μορφής |f(x)| = g(x).

Ασκήσεις

Α' ΟΜΑΔΑΣ
1.	Να λύσετε τις εξισώσεις
2.	Να λύσετε τις εξισώσεις
3.	Να λύσετε τις εξισώσεις για τις διάφορες τιμές της παραμέτρου λ R
4.	Στο παρακάτω ορθογώνιο τραπέζιο να βρεθεί η θέση του σημείου Μ στην ΑΔ ώστε για τα εμβαδά
5.	Από κεφάλαιο 4000 € ένα μέρος του κατατέθηκε σε μια τράπεζα προς 5% και το υπόλοιπο σε μια άλλη τράπεζα προς 3%. Ύστερα από 1 χρόνο εισπράχθηκαν συνολικά 175€ τόκοι. Ποιο ποσό τοκίστηκε προς 5% και ποιο προς 3%;
6.	Να επιλυθούν οι παρακάτω τύποι ως προς την αναφερόμενη μεταβλητή:
7.	Να λύσετε τις εξισώσεις i) x² (x – 4) + 2x(x – 4) + (x – 4) = 0. ii) (x – 2 )² – (2 – x) (4 + x) = 0.
8.	Να λύσετε τις εξισώσεις i) x(x² –1) – x³ + x² = 0 ii) (x +1)² + x² – 1 = 0
9.	Να λύσετε τις εξισώσεις i) x(x – 2)² = x² – 4x + 4 ii) (x² – 4)(x – 1) = (x² – 1)(x – 2).
10.	Να λύσετε τις εξισώσεις i) x³ – 2x² – x + 2 = 0 ii) x³ – 2x² – (2x –1)(x – 2) = 0.
11.	Να λύσετε τις εξισώσεις
12.	Να λύσετε τις εξισώσεις
13.	Να βρείτε τρεις διαδοχικούς ακέραιους τέτοιους ώστε το άθροισμα τους να ισούται με το γινόμενο τους.
14.	Να λύσετε τις εξισώσεις
15.	Να λύσετε τις εξισώσεις
16.	Να λύσετε τις εξισώσεις

B' ΟΜΑΔΑΣ
1.	Να αποδείξετε ότι οι εξισώσεις: έχουν πάντα λύση, οποιοιδήποτε και αν είναι οι πραγματικοί αριθμοί α, β.
2.	Ποιοί περιορισμοί πρέπει να ισχύουν για τα α, β R , ώστε να έχει λύση η εξίσωση
3.	Πόσο καθαρό οινόπνευμα πρέπει να προσθέσει ένας φαρμακοποιός σε 200ml διάλυμα οινοπνεύματος περιεκτικότητας 15%, για να πάρει διάλυμα οινοπνεύματος περιεκτικότητας 32%;
4.	Ένα αυτοκίνητο Α κινείται με 100km/h. Ένα δεύτερο αυτοκίνητο Β που κινείται με 120km/h προσπερνάει το Α. Σε πόσα λεπτά τα δυο αυτοκίνητα θα απέχουν 1km;
5.	Να λύσετε την εξίσωση για όλες τις τιμές του α R
6.	Να λύσετε την εξίσωση
7.	Να λύσετε την εξίσωση \|2\|x\|–1\| = 3
8.	Να λύσετε την εξίσωση