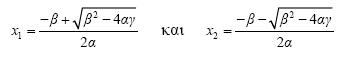|
ΙΣΤΟΡΙΚΟ ΣΗΜΕΙΩΜΑ
Από τα αρχαία χρόνια οι μαθηματικοί χρησιμοποίησαν διάφορες τεχνικές για να λύσουν μια εξίσωση 2ου βαθμού.
Οι αρχαίοι Έλληνες χρησιμοποίησαν γεωμετρικές μεθόδους, ίσως λόγω των δυσκολιών που είχαν με τους άρρητους αριθμούς, αλλά και λόγω πρακτικών δυσκολιών που προέκυπταν από τα ελληνικά ψηφία.
Οι Ινδοί και οι Άραβες χρησιμοποίησαν μια μέθοδο όμοια με τη σημερινή διαδικασία «συμπλήρωσης τετραγώνου», περιγράφοντας όμως λεκτικά τον τρόπο εύρεσης των λύσεων. Αυτοί θεωρούσαν ως διαφορετικού τύπου κάθε μία από τις εξισώσεις
x2 + px = q, x2 – px = q, x2
– px = –q .
Σήμερα όμως γράφουμε τις εξισώσεις αυτές με τη γενική μορφή
αx2 + βx + γ = 0
Ο σύγχρονος συμβολισμός άρχισε να εμφανίζεται περί το 1500 μ.Χ, και οι δυνατότητες χρησιμοποίησης αρνητικών ριζών και ακόμα μιγαδικών ριζών προτάθηκαν από τους Cardano και Girard. Η γεωμετρική παράσταση των αρνητικών ριζών από τον Descartes και των μιγαδικών αριθμών από τούς Wessel, Argand και Gauss έκαμε τους αριθμούς αυτούς περισσότερο αποδεκτούς ως ρίζες μιας δευτεροβάθμιας εξίσωσης.
Όμως η ποικιλία των επιλύσεων που αναπτύχθηκε τα αρχαία χρόνια μας ενέπνευσε να αναπτύξουμε μερικούς τρόπους εξαγωγής του τύπου
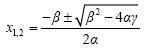
που δίνει τις ρίζες της γενικής εξίσωσης 2ου βαθμού
αx2 + βx + γ = 0, α ≠ 0 .
Στη συνέχεια παρουσιάζουμε τρεις μεθόδους επίλυσης μίας εξίσωσης 2ου βαθμού.
Μέθοδος των Ινδών
Η επίλυση αυτή που επινοήθηκε στην Ινδία, αποδίδεται στον Sridhara (1025 μ. Χ. περίπου).
Έχουμε διαδοχικά:
αx2 + βx + γ = 0
αx2 + βx = –γ
Πολλαπλασιάζουμε και τα δύο μέλη της εξίσωσης με 4α και ύστερα προσθέτουμε το β2 και στα δύο μέλη, για να προκύψει ένα «τέλειο» τετράγωνο στο αριστερό μέλος. Δηλαδή
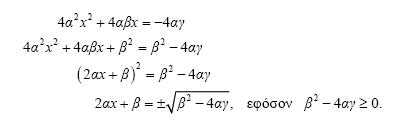
Έτσι προκύπτει ότι:
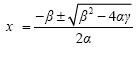
Σχόλιο: Η απλότητα της μεθόδου των Ινδών χαρακτηρίζεται από το γεγονός ότι το κλάσμα δεν εμφανίζεται. παρά μόνο στο τελευταίο βήμα.
Μέθοδος του Vieta
Η εξίσωση 2ου βαθμού αx2 + βx + γ = 0, α ≠ 0 μπορεί να λυθεί ευκολότερα, αν δεν περιέχει τον πρωτοβάθμιο όρο βx, πράγμα που μπορεί εύκολα να επιτευχθεί με την αντικατάσταση
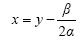
Τότε η εξίσωση γίνεται:
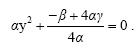 η οποία όταν απλοποιηθεί γίνεται: η οποία όταν απλοποιηθεί γίνεται:
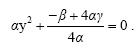
Οι ρίζες της εξίσωσης αυτής είναι
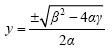 εφόσον β2
– 4αγ ≥ 0 εφόσον β2
– 4αγ ≥ 0
Για να βρούμε τις ρίζες της αρχικής εξίσωσης αντικαθιστούμε την παραπάνω τιμή του y στην (1) και έχουμε:
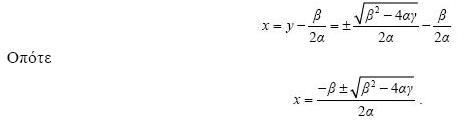
Σχόλιο: Η μέθοδος αυτή του Vieta είναι ενδιαφέρουσα, γιατί είναι ο προάγγελος της τεχνικής για την επίλυση της γενικής τριτοβάθμιας καθώς και της διτετράγωνης εξίσωσης. Για παράδειγμα, το πρώτο βήμα στην επίλυση της
εξίσωσης αx3 + βx2 + γx + δ = 0, είναι η αντικατάσταση
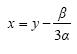 που απαλλάσσει την εξίσωση από το δευτεροβάθμιο όρο. που απαλλάσσει την εξίσωση από το δευτεροβάθμιο όρο.
Μέθοδος του Harriot
Ο μαθηματικός Thomas Harriot (1560–1621) εφάρμοσε τη μέθοδο της παραγοντοποίησης, για να βρει τις λύσεις μιας εξίσωσης 2ου βαθμού, στο μεγάλο έργο του για την άλγεβρα «Artis Analytical Praxis». Η τεχνική του είναι η εξής περίπου:
Υποθέτουμε ότι x1 και x2 είναι οι ρίζες της δευτεροβάθμιας εξίσωσης
αx2 + βx + γ = 0, α ≠ 0 (1).
Σχηματίζουμε τώρα μία εξίσωση με ρίζες x1 και x2. Αυτή είναι η (x
– x1 )(x – x2 ) = 0 ή ,ισοδύναμα, η
x2 – (x1 + x2) x + x2 x2 = 0 (2)
Με διαίρεση των μελών της (1) με α ≠ 0 , βρίσκουμε:
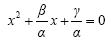 (3) (3)
Επειδή οι εξισώσεις (2) και (3) είναι ίδιες, οι αντίστοιχοι συντελεστές πρέπει να είναι ίσοι. Επομένως:
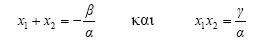 (4) (4)
Η ταυτότητα (x1 – x2 )2 = (x1 + x2 )2
– 4x1 x2 σε συνδυασμό με την (4) δίνει
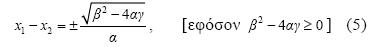
Λύνοντας το σύστημα των εξισώσεων (4) και (5) έχουμε:
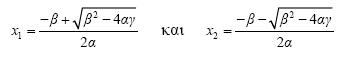
Σχόλιο: Είναι αρκετό να θεωρήσουμε μόνο τη θετική τετραγωνική ρίζα της (5). Η αρνητική ρίζα απλώς εναλλάσσει τη διάταξη των x1 και x2.
| ![]() ,
όπου S το διάστημα που διανύει κινητό σε χρόνο t, με
αρχική ταχύτητα v0 και επιτάχυνση γ. Αν
θεωρήσουμε ως άγνωστο τον χρόνο t, τότε προκύπτει η εξίσωση:
,
όπου S το διάστημα που διανύει κινητό σε χρόνο t, με
αρχική ταχύτητα v0 και επιτάχυνση γ. Αν
θεωρήσουμε ως άγνωστο τον χρόνο t, τότε προκύπτει η εξίσωση:![]()
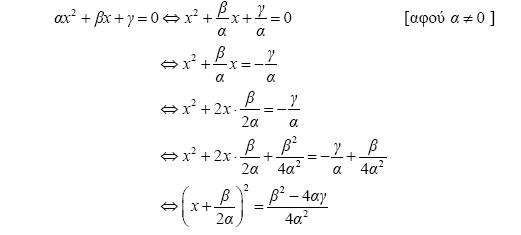

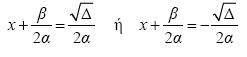
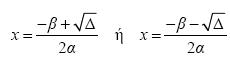
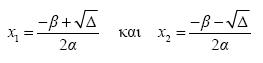
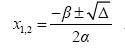 .
.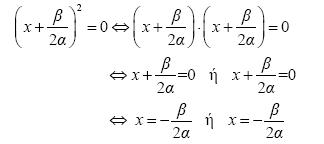
![]()
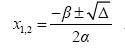
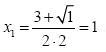 και
και
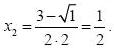
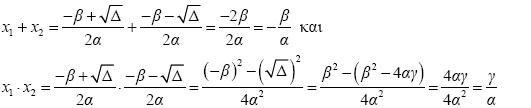
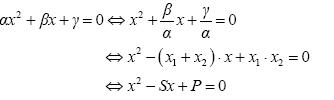
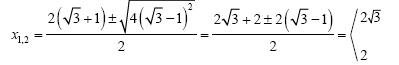
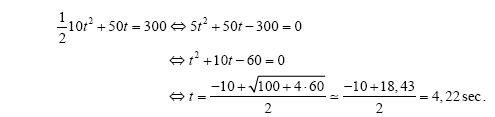
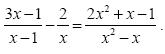
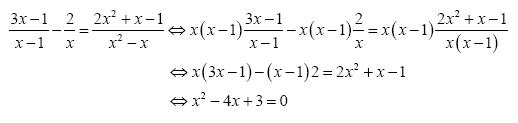
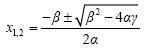
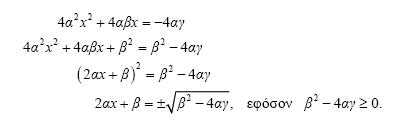
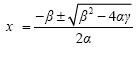
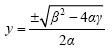 εφόσον β2
– 4αγ ≥ 0
εφόσον β2
– 4αγ ≥ 0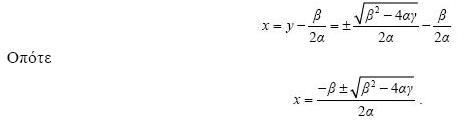
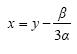 που απαλλάσσει την εξίσωση από το δευτεροβάθμιο όρο.
που απαλλάσσει την εξίσωση από το δευτεροβάθμιο όρο.