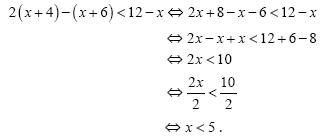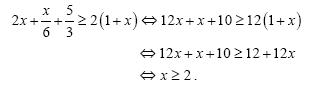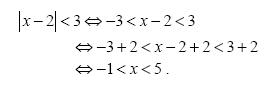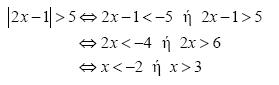ΑΝΙΣΩΣΕΙΣ

Οι ανισώσεις: αx + β > 0 και αx + β < 0

Γνωρίσαμε στο Γυμνάσιο τη διαδικασία επίλυσης μιας ανίσωσης της μορφής αx + β > 0 ή της μορφής αx + β < 0 , με α και β συγκεκριμένους αριθμούς.

Γενικότερα έχουμε:

αx + β > 0 <=> αx + β – β > –β
<=>αx > –β

Διακρίνουμε τώρα τις εξής περιπτώσεις:

Αν α > 0, τότε:

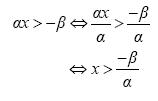
Αν α < 0, τότε:

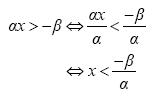
Αν α = 0, τότε η ανίσωση γίνεται 0x > –β, η οποία

αληθεύει για κάθε x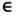R, αν είναι β > 0, ενώ

είναι αδύνατη, αν είναι β < 0 .

Για παράδειγμα:

Η ανίσωση 4x > 8 γράφεται:

Επομένως η ανίσωση αυτή αληθεύει για x (2, +∞)

Η ανίσωση –4x > 8 γράφεται:

Επομένως η ανίσωση αυτή αληθεύει για x (–∞,–2).

Η ανίσωση 0x > –2 αληθεύει για κάθε x 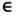R , ενώ η ανίσωση 0x > 2 είναι αδύνατη.

ΕΦΑΡΜΟΓΗ

i) Να λυθούν οι ανισώσεις:

ii) Να βρεθούν οι κοινές λύσεις των δύο ανισώσεων.

ΛΥΣΗ

i) Για την πρώτη ανίσωση έχουμε:

Άρα η ανίσωση αληθεύει για κάθε πραγματικό αριθμό x < 5 .

Για τη δεύτερη ανίσωση έχουμε:

Άρα η ανίσωση αληθεύει για κάθε πραγματικό αριθμό x ≥ 2

ii) Επειδή η πρώτη ανίσωση αληθεύει για x < 5 και η δεύτερη για x ≥ 2, οι ανισώσεις συναληθεύουν για κάθε πραγματικό αριθμό x με 2 ≤ x ≤ 5 , δηλαδή οι ανισώσεις συναληθεύουν όταν x [2,5).

Για τον προσδιορισμό των κοινών λύσεων των δύο ανισώσεων μας διευκολύνει να παραστήσουμε τις λύσεις τους στον ίδιο άξονα (Σχήμα), απ’ όπου προκύπτει ότι 2 ≤ x ≤ 5

Ανισώσεις με απόλυτες τιμές

Με τη βοήθεια των ιδιοτήτων της απόλυτης τιμής και της έννοιας της απόστασης δύο αριθμών, μπορούμε να επιλύουμε ανισώσεις που περιέχουν απόλυτες τιμές. Στη συνέχεια θα δούμε μερικά παραδείγματα επίλυσης τέτοιων ανισώσεων.

ΠΑΡΑΔΕΙΓΜΑ 1^ο/

Να λυθεί η ανίσωση: |x – 2| < 3 .

ΛΥΣΗ/

Η επίλυση της ανίσωσης |x – 2| < 3,με τη βοήθεια της ιδιότητας

|x – x_ο| < ρ <=> x_ο – ρ < x < x_ο + ρ

γίνεται ως εξής:

|x – 2| < 3 <=> 2 – 3 < x < 2 + 3
<=> –1 < x < 5

Μπορούμε όμως να λύσουμε την παραπάνω ανίσωση και με τη βοήθεια της ιδιότητας

|x| < ρ<=> –ρ < x < ρ

ως εξής:

Άρα η ανίσωση αληθεύει για x (–1,5).

ΠΑΡΑΔΕΙΓΜΑ 2^ο/

Να λυθεί η ανίσωση: |2x –1| > 5

ΛΥΣΗ/

Από την ιδιότητα |x| > ρ <=> x < –ρ ή x > ρ έχουμε :

Άρα η ανίσωση αληθεύει για x (–∞,–2) U (3,+∞).

Ασκήσεις

Α' ΟΜΑΔΑΣ
1.	Να λύσετε τις ανισώσεις:
2.	Να βρείτε τις τιμές του x για τις οποίες συναληθεύουν οι ανισώσεις
3.	Να εξετάσετε αν συναληθεύουν οι ανισώσεις:
4.	Να βρείτε τα x Z για τα οποία συναληθεύουν οι ανισώσεις:
5.	Να λύσετε τις ανισώσεις: i) \|x\| < 3 ii) \|x –1\| ≤ 4 iii) \|2x +1\| < 5
6.	Να λύσετε τις ανισώσεις: i) \|x\| ≥ 3 ii) \|x – 1\| > 4 iii) \|2x +1\| ≥ 5.
7.	Να λύσετε τις εξισώσεις: i) \|2x – 6\| = 2x – 6 ii) \|3x –1\| = 1 – 3x.
8.	Να λύσετε τις ανισώσεις:
9.	Να λύσετε την ανίσωση
10.	Να βρείτε την ανίσωση της μορφής \|x – x₀\| < ρ, που έχει ως λύσεις τους αριθμούς του διαστήματος (–7,3).
11.	Η σχέση που συνδέει τους βαθμούς Κελσίου (^oC) με τους βαθμούς Φαρενάϊτ (^oF) είναι η . Στη διάρκεια μιας νύχτας η θερμοκρασία σε μια πόλη κυμάνθηκε από 41^oF μέχρι 50^oF. Να βρείτε το διάστημα μεταβολής της θερμοκρασίας σε ^oC.

B' ΟΜΑΔΑΣ
1.	Να βρείτε τις τιμές x για τις οποίες ισχύει: i) 3 ≤ 4x –1 ≤ 6 ii) –4 ≤ 2 – 3x ≤ –2.
2.	Να βρείτε τις τιμές x για τις οποίες ισχύει: i) 2 ≤ \|x\| ≤ 4 ii) 2 ≤ \|x – 5\| ≤ 4.
3.	Έστω Α και Β τα σημεία που παριστάνουν σε έναν άξονα τους αριθμούς –3 και 5 και Μ το μέσο του τμήματος ΑΒ. i) Ποιος αριθμός αντιστοιχεί στο σημείο Μ; ii) Να διατυπώσετε γεωμετρικά το ζητούμενο της ανίσωσης \|x – 5\| ≤ \|x + 3\| και να βρείτε τις λύσεις της. iii) Να επιβεβαιώσετε αλγεβρικά τα συμπεράσματά σας.
4.	Έστω Α και Β τα σημεία που παριστάνουν σε έναν άξονα τους αριθμούς 1 και 7 και Μ το μέσο του τμήματος ΑΒ. i) Ποιος αριθμός αντιστοιχεί στο σημείο Μ; ii) Να διατυπώσετε γεωμετρικά το ζητούμενο της εξίσωσης \|x – 1\| + \|x – 7\| = 6 και να βρείτε τις λύσεις της. iii) Να επιβεβαιώσετε αλγεβρικά τα συμπεράσματά σας, αφού προηγουμένως συντάξετε πίνακα προσήμου των παραστάσεων x – 1 και x – 7 .