Μορφές τριωνύμου
Η παράσταση αx2 + βx + γ, α = 0 λέγεται τριώνυμο 2ου βαθμού ή, πιο απλά, τριώνυμο. Η διακρίνουσα Δ της αντίστοιχης εξίσωσης αx2 + βx + γ = 0 λέγεται και διακρίνουσα του τριωνύμου. Οι ρίζες της εξίσωσης αx2 + βx + γ = 0, δηλαδή οι
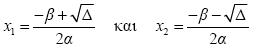 ονομάζονται και ρίζες του τριωνύμου.
ονομάζονται και ρίζες του τριωνύμου.
Το τριώνυμο αx2 + βx + γ, α ≠ 0 μετασχηματίζεται ως εξής:
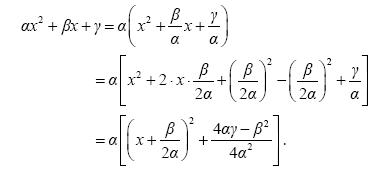
Επομένως:
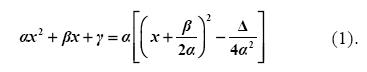
Διακρίνουμε τώρα τις εξής περιπτώσεις:
- Δ > 0 . Τότε ισχύει
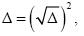 , οπότε έχουμε:
, οπότε έχουμε:
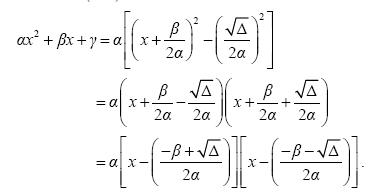
Επομένως:
αx2 + βx + γ = α(x – x1)(x – x2) ,
όπου x1, x2 οι ρίζες του τριωνύμου.
Άρα, όταν Δ > 0, τότε το τριώνυμο μετατρέπεται σε γινόμενο του α επί δύο πρωτοβάθμιους παράγοντες.
- Δ = 0 . Τότε από την ισότητα (1) έχουμε:
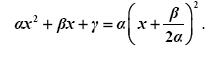
Άρα, όταν Δ = 0, τότε το τριώνυμο μετατρέπεται σε γινόμενο του α επί ένα τέλειο τετράγωνο.
- Δ < 0 . Τότε ισχύει |Δ| = –Δ, οπότε έχουμε:
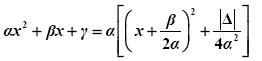
Επειδή για κάθε x
![]() R , η παράσταση μέσα στην αγκύλη είναι θετική, το τριώνυμο δεν αναλύεται σε γινόμενο πρωτοβάθμιων παραγόντων.
R , η παράσταση μέσα στην αγκύλη είναι θετική, το τριώνυμο δεν αναλύεται σε γινόμενο πρωτοβάθμιων παραγόντων.
Συνοψίζοντας τα παραπάνω συμπεράσματα για τις μορφές του τριωνύμου αx2 + βx + γ, α ≠ 0 με διακρίνουσα Δ έχουμε:
αx2 + βx + γ = α(x – x1 )(x – x2), όπου x1, x2 οι ρίζες του τριωνύμου.
|
Για παράδειγμα:
- Το τριώνυμο 2x2 + 3x – 2 έχει Δ = 9 + 16 = 25 > 0 και ρίζες
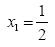 και x2 =
–2. Επομένως:
και x2 =
–2. Επομένως:
![]()
- Το τριώνυμο
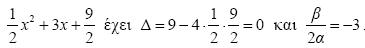 . Eπομένως:
. Eπομένως:
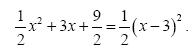
- Το τριώνυμο 2x2 – 6x + 5 έχει Δ= – 4 < 0 . Επομένως:
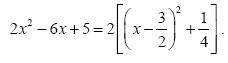
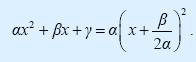
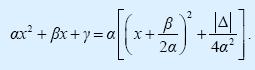
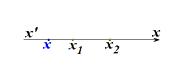
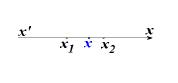
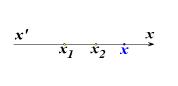
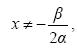 , ενώ μηδενίζεται για
, ενώ μηδενίζεται για
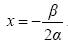
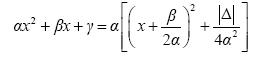
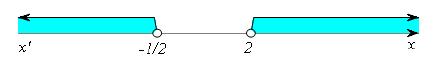
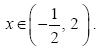 . Οι λύσεις αυτές εποπτικά φαίνονται στο παρακάτω σχήμα.
. Οι λύσεις αυτές εποπτικά φαίνονται στο παρακάτω σχήμα.

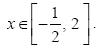 . Οι λύσεις αυτές εποπτικά φαίνονται στο παρακάτω σχήμα.
. Οι λύσεις αυτές εποπτικά φαίνονται στο παρακάτω σχήμα.


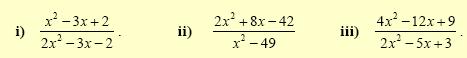
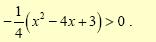
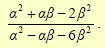
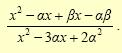
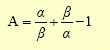 για τις διάφορες τιμές των α,
β ≠ 0 .
για τις διάφορες τιμές των α,
β ≠ 0 .