4.3 ΑΝΙΣΩΣΕΙΣ ΓΙΝΟΜΕΝΟ & ΑΝΙΣΩΣΕΙΣ ΠΗΛΙΚΟ
Πρόσημο γινομένου
Έστω ότι θέλουμε να μελετήσουμε ένα γινόμενο P(x) = Α(x) · Β(x) · … · Φ(x) ως προς το πρόσημό του, όπου οι παράγοντες Α(x), Β(x) , … , Φ(x) είναι της μορφής αx + β (πρωτοβάθμιοι) ή της μορφής αx2 + βx + γ (τριώνυμα).
Βρίσκουμε το πρόσημο κάθε παράγοντα χωριστά και στη συνέχεια το πρόσημο του P(x), όπως φαίνεται στο παράδειγμα που ακολουθεί.
ΠΑΡΑΔΕΙΓΜΑ
Να βρεθεί για τις διάφορες τιμές του x![]() R το πρόσημο του γινομένου
R το πρόσημο του γινομένου
P(x) = (x – 1) (x2 + x – 6)(2x2 + x + 1) .
ΛΥΣΗ
Αρχικά βρίσκουμε το πρόσημο του κάθε παράγοντα χωριστά ως εξής:
- Επειδή
x – 1 ≥ 0 <=> x ≥ 1,
το x – 1 είναι θετικό για x > 1, μηδέν για x = 1 και αρνητικό για x < 1.
- Επειδή
x2 + x – 6 ≥ 0<=> (x + 3)(x – 2) ≥ 0 <=> x ≤ –3 ή x ≥ 2,
το x2 + x – 6 είναι θετικό για x < –3 και για x > 2 , μηδέν για x = –3 και για x = 2 και αρνητικό για –3 < x < 2 .
- Επειδή το 2x2 + x +1 έχει διακρίνουσα Δ = 1 – 8 = –7 < 0, το τριώνυμο αυτό είναι θετικό για κάθε x
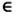 R .
R .
Ο προσδιορισμός, τώρα, του προσήμου του γινομένου P(x) γίνεται με τη βοήθεια του παρακάτω πίνακα, εφαρμόζοντας τον κανόνα των προσήμων.
| x | –∞ –3 1 2 +∞ |
|---|---|
| x –1 | – | – 0 + | + |
| x2 + x – 6 | + 0 – | – 0 + |
| 2x2 + x + 1 | + | + | + | + |
| P(x) | – 0 + 0 – 0 + |
Ώστε το γινόμενο P(x) είναι θετικό για –3 < x < 1 και για x > 2, ενώ είναι αρνητικό για x < –3 και για 1 < x < 2. Τέλος είναι μηδέν για x = –3, για x = 1 και για x = 2 .
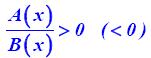
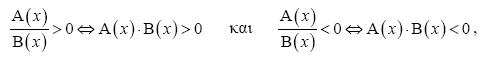
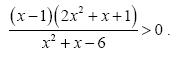
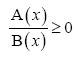 αληθεύει για εκείνους τους πραγματικούς αριθμούς x για τους οποίους ισχύουν συγχρόνως
αληθεύει για εκείνους τους πραγματικούς αριθμούς x για τους οποίους ισχύουν συγχρόνως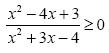 . Έχουμε:
. Έχουμε: