Πρόοδοι

5.1 Ακολουθίες

Η έννοια της ακολουθίας

Ας υποθέσουμε ότι καταθέτουμε στην τράπεζα ένα κεφάλαιο 10000 ευρώ με ανατοκισμό ανά έτος και με επιτόκιο 2%. Αυτό σημαίνει ότι σε ένα χρόνο οι τόκοι που θα αποδώσει το κεφάλαιο προστίθενται σε αυτό και το ποσό που προκύπτει ξανατοκίζεται για τον επόμενο χρόνο με το ίδιο επιτόκιο. Η διαδικασία αυτή μπορεί να συνεχιστεί όσα χρόνια θέλουμε. Επομένως, το κεφάλαιο των 10000 ευρώ θα γίνει:

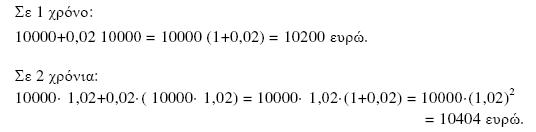
Συνεχίζοντας με τον ίδιο τρόπο βρίσκουμε ότι το ποσό των 10000 ευρώ θα γίνει:

Σε 3 χρόνια 10000 (1,02)4 ευρώ, σε 4 χρόνια 10000•(1,02)⁴ ευρώ κτλ. και σε ν χρόνια θα γίνει 10000(1,02 )^ν ευρώ.

Έτσι έχουμε τον πίνακα:

Παρατηρούμε ότι κάθε θετικός ακέραιος ν αντιστοιχίζεται στον πραγματικό αριθμό 10000•(1,02)^ν.

Η παραπάνω αντιστοίχιση ονομάζεται ακολουθία πραγματικών αριθμών.

Γενικά ακολουθία πραγματικών αριθμών είναι μια αντιστοίχιση των φυσικών αριθμών 1,2,3,…,ν,… στους πραγματικούς αριθμούς. Ο αριθμός στον οποίο αντιστοιχεί ο 1 καλείται πρώτος όρος της ακολουθίας και τον συμβολίζουμε συνήθως με α₁, ο αριθμός στον οποίο αντιστοιχεί ο 2 καλείται δεύτερος όρος της ακολουθίας και τον συμβολίζουμε συνήθως με α2 κ.λ.π. Γενικά ο αριθμός στον οποίο αντιστοιχεί ένας φυσικός αριθμός ν καλείται ν–οστός ή γενικός όρος της ακολουθίας και το συμβολίζουμε συνήθως με α_ν. Δηλαδή, 1→ α₁, 2→ α₂, 3→α₃, …, ν→α_ν, … Την ακολουθία αυτή τη συμβολίζουμε (α_ν).

Παραδείγματα.

1. Η αντιστοίχιση 1→1², 2→2²,... ν→ν²,... είναι η ακολουθία (αν) με πρώτο όρο α₁=1², δεύτερο όρο α₂=2² κλπ. και γενικό όρο α_ν=ν².
2. Η ακολουθία (α_ν) με γενικό όρο α_ν= (–1)^ν έχει όρους: α₁=–1, α₂=1, α₃= –1,…
3. 

Ακολουθίες που ορίζονται αναδρομικά

Στην ακολουθία 1², 2², 3², ..., ν²,... ο γενικός της όρος α_ν = ν² μας επιτρέπει να βρούμε τον οποιονδήποτε όρο της. Είναι π.χ. α₂₀ = 20² = 400, α₁₀₀ = 100² = 10000 κτλ.

Υπάρχουν όμως και ακολουθίες που για το γενικό τους όρο είναι δύσκολο να βρεθεί ένας μαθηματικός τύπος

Ας θεωρήσουμε π.χ. την ακολουθία (α_ν), της οποίας ο πρώτος όρος είναι το 1, ο δεύτερος όρος είναι επίσης το 1 και κάθε άλλος όρος, από τον τρίτο και μετά, είναι ίσος με το άθροισμα των δυο προηγούμενων όρων:

Έχουμε:

Παρατηρούμε ότι μπορούμε με διαδοχικά βήματα να βρούμε τον οποιονδήποτε όρο της ακολουθίας. Αυτό σημαίνει ότι η ακολουθία (α_ν) είναι τελείως ορισμένη.

Λέμε ότι η ακολουθία (α_ν) ορίζεται αναδρομικά και η ισότητα α_ν+2 = α_ν+1+α_ν λέγεται αναδρομικός τύπος της ακολουθίας. Γενικότερα, για να ορίζεται μια ακολουθία αναδρομικά, απαιτείται να γνωρίζουμε:

1. Τον αναδρομικό της τύπο και
2. Όσους αρχικούς όρους μας χρειάζονται, ώστε ο αναδρομικός τύπος να αρχίσει να δίνει όρους.

Σχόλιο: Υπάρχουν ακολουθίες, για τις οποίες μέχρι τώρα δε γνωρίζουμε ούτε έναν τύπο για το γενικό τους όρο ούτε έναν αναδρομικό τύπο. Μια τέτοια ακολουθία είναι π.χ. η ακολουθία των πρώτων αριθμών:

2, 3, 5, 7, 11, 13,...

Γραφική παράσταση ακολουθίας

ΠΑΡΑΔΕΙΓΜΑΤΑ

1ο Να γράψετε τους τέσσερις πρώτους όρους και τους 20ους όρους των ακολουθιών

ΛΥΣΗ

2ο Δίνεται η ακολουθία με α = 2 και α = α² + 1. Να βρεθούν οι πρώτοι τέσσερις όροι της ακολουθίας

ΛΥΣΗ

3ο Δίνεται η ακολουθία α_ν = 3ν+5. Να οριστεί η ακολουθία αυτή και αναδρομικά.

ΛΥΣΗ

ΑΣΚΗΣΕΙΣ

Α' ΟΜΑΔΑΣ

ΑΣΚΗΣΕΙΣ

B' ΟΜΑΔΑΣ

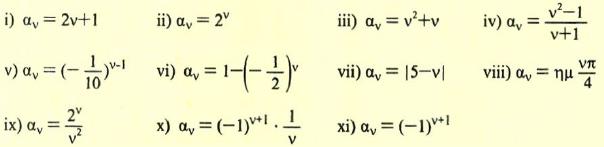
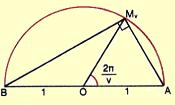
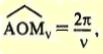1.	Το σημείο Μν κινείται στο ημικύκλιο κέντρου Ο και ακτίνας ,1 έτσι, ώστε θετικός ακέραιος μεγαλύτερος της μονάδας. Να βρείτε το γενικό όρο της ακολουθίας (αν), της οποίας κάθε όρος εκφράζει το μήκος του ΑΜν. /td>
2.	Θεωρούμε την ευθεία y = x + 1 και την ακολουθία (αν), της οποίας ο όρος αν εκφράζει το γραμμοσκιασμένο εμβαδό. Να βρείτε το αν .
3.	Θεωρούμε την ακολουθία Να χαράξετε τη γραφική παράσταση της συνάρτησης εξηγήσετε στο σχήμα τι παριστάνει η ακολουθία ( αν ). Να αποδείξετε ότι για την ακολουθία αυτή ισχύει αν+1 < αν .
4.	Να βρείτε το ν° όρο της ακολουθίας με α1 = 1 και αν = ν · αν
5.	Αν δοθεί ένας αριθμός Α > 0, τότε αποδεικνύεται ότι οι διαδοχικοί όροι της ακολουθίας με προσεγγίζουν όλο και περισσότερο την καθώς το ν μεγαλώνει. Να βρείτε μια προσέγγιση της υπολογίζοντας τον α4. (Να συγκρίνετε το αποτέλεσμα με την τιμή της που δίνουν οι πίνακες).
6.	Κάθε πλευρά ενός ισόπλευρου τριγώνου χωρίζεται σε τρία ίσα τμήματα. Το μεσαίο τμήμα κάθε πλευράς αντικαθίσταται από τις δυο πλευρές ισόπλευρου τριγώνου. Στο σχήμα με μορφή αστεριού που προκύπτει αντικαθιστούμε πάλι το μεσαίο κάθε πλευράς με δυο πλευρές ισόπλευρου τριγώνου. Με ανάλογο τρόπο συνεχίζουμε για κάθε σχήμα που προκύπτει από τη διαδικασία αυτή. Να βρείτε έναν αναδρομικό τύπο και το γενικό όρο της ακολουθίας (Sv) που εκφράζει το πλήθος των πλευρών κάθε σχήματος. Να βρείτε έναν αναδρομικό τύπο και το γενικό όρο της ακολουθίας (Uv) που εκφράζει την περίμετρο κάθε σχήματος, αν το αρχικό ισόπλευρο τρίγωνο έχει πλευρά ίση με 1.