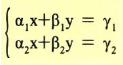Πρόοδοι

5.2 Αριθμητική πρόοδος

–Στην ακολουθία 1, 3, 5, 7,... των περιττών αριθμών, κάθε όρος προκύπτει από τον προηγούμενό του με πρόσθεση του αριθμού 2. Δηλαδή για την ακολουθία αυτή ισχύει:

Η ακολουθία (α_ν) λέγεται αριθμητική πρόοδος με διαφορά 2.

–Στην ακολουθία 15, 10, 5, 0, –5, –10,... κάθε όρος προκύπτει από τον προηγούμενό του με πρόσθεση του αριθμού –5. Δηλαδή για την ακολουθία αυτή ισχύει:

Όπως και προηγουμένως, η ακολουθία (α_ν) λέγεται αριθμητική πρόοδος με διαφορά –5.

Γενικότερα ορίζουμε ότι:

Μια ακολουθία λέγεται αριθμητική πρόοδος, αν κάθε όρος της προκύπτει από τον προηγούμενό του με πρόσθεση του ίδιου πάντοτε αριθμού.

Τον αριθμό αυτό τον συμβολίζουμε με ω και τον λέμε διαφορά της προόδου.

Επομένως, η ακολουθία (α_ν) είναι αριθμητική πρόοδος με διαφορά ω, αν και μόνο αν ισχύει:

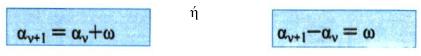
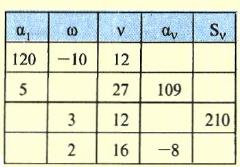
Αν σε μια αριθμητική πρόοδο γνωρίζουμε τον πρώτο όρο της α1 και τη διαφορά της ω τότε ο αναδρομικός της τύπος α_ν+1 = α_ν+ω μας επιτρέπει να βρούμε με διαδοχικά βήματα τον οποιονδήποτε όρο της.

Μπορούμε όμως να υπολογίσουμε κατευθείαν το ν= όρο α_ν μιας αριθμητικής προόδου ως συνάρτηση των α1. ω και ν ως εξής: Από τον ορισμό της αριθμητικής προόδου έχουμε:

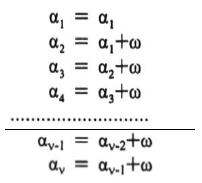
Προσθέτοντας κατά μέλη της ν αυτές ισότητες και εφαρμόζοντας την ιδιότητα της διαγραφής βρίσκουμε α_ν=α₁+(ν–1)ω

Επομένως

Έτσι π.χ. στην αριθμητική πρόοδο 3, 5, 7, 9 ................ η οποία έχει α, = 3 και ω=5–3=2, ο ν = όρος της είναι α_ν = 3+(ν–1) 2. Επομένως ο 20ος όρος της είναι α₂₀ = 3+19 · 2 = 41, ο 100 όρος της είναι α₁₀₀ = 3+99–2 = 201 κτλ.

Αριθμητικός μέσος

Αν πάρουμε τρεις διαδοχικούς όρους α, β, γ μιας αριθμητικής προόδου με διαφορά ω, τότε ισχύει:

Αλλά και αντιστρόφως, αν για τρεις αριθμούς α, β, γ ισχύει τότε έχουμε

που σημαίνει ότι οι α, β, γ είναι διαδοχικοί όροι αριθμητικής προόδου. Ο β λέγεται αριθμητικός μέσος των α και γ

Αποδείξαμε λοιπόν ότι:

Άθροισμα ν διαδοχικών όρων αριθμητικής προόδου

Ας θεωρήσουμε την αριθμητική πρόοδο 1, 2, 3, 4,... και ας βρούμε το άθροισμα των 100 πρώτων όρων της

Αντί να προσθέσουμε τους αριθμούς αυτούς με τον συνήθη τρόπο, μπορούμε να βρούμε συντομότερα το άθροισμά τους ως εξής:

Γράφουμε δυο φορές το παραπάνω άθροισμα, αλλά με αντίθετη τη σειρά των προσθετέων και προσθέτουμε τις δυο ισότητες κατά μέλη:

Εφαρμόζοντας τον παραπάνω τρόπο σε μια οποιαδήποτε αριθμητική πρόοδο, θα αποδείξουμε ότι:

ΑΠΟΔΕΙΞΗ

ΠΑΡΑΔΕΙΓΜΑΤΑ

1ο Να βρεθεί το άθροισμα 7+10+13 +...+ 157

ΛΥΣΗ

Πρόκειται για το άθροισμα διαδοχικών όρων μιας αριθμητικής προόδου με α₁ = 7, α_ν = 157 και ω = 3. Για να το υπολογίσουμε, χρειαζόμαστε το πλήθος ν των προσθετέων. Από τον τύπο του ν όρου α_ν = α₁+(ν–1)ω έχουμε

Επομένως το ζητούμενο άθροισμα είναι

2ο Πόσοι όροι της αριθμητικής προόδου 52, 47, 42,... έχουν άθροισμα ίσο με 90;

ΛΥΣΗ

Επειδή όμως v N^*, συμπεραίνουμε ότι ν = 20. Άρα 20 όροι της δοθείσης αριθμητικής προόδου έχουν άθροισμα ίσο με 90.

3ο Ο 10^ος όρος μιας αριθμητικής προόδου είναι ο 42 και ο 19^ος όρος της είναι ο 87. Να υπολογισθεί το άθροισμα των πρώτων 100 όρων της προόδου αυτής.

ΛΥΣΗ

Από τον τύπο α_ν = α₁+(ν–1)ω έχουμε 42 =α₁+ 9ω και 87= α₁+ 18ω. Επομένως οι α και ω είναι οι λύσεις του συστήματος

Από την επίλυση του συστήματος αυτού βρίσκουμε ότι είναι α, = –3 και ω = 5.

ΑΣΚΗΣΕΙΣ

Α' ΟΜΑΔΑΣ

1.	Να βρείτε το ν^o όρο των αριθμητικών προόδων:

2.	Να βρείτε το ζητούμενο όρο σε καθεμιά από τις αριθμητικές προόδους:

3.	i) Αν ο 6= όρος μιας αριθμητικής προόδου είναι 12 και ο 10 όρος είναι 16, να βρείτε τον 1° όρο και τη διαφορά της προόδου.
	Ομοίως, αν είναι α₅ = 14 και α₁₂ = 42 Ομοίως, αν είναι α₃ = 20 και α₇ = 32.
4.	Ο 5ος όρος μιας αριθμητικής προόδου είναι –5 και ο 15 = όρος της είναι –2. Να βρείτε τον 50° όρο της προόδου. Αν σε μια αριθμητική πρόοδο είναι α₇ = 55 και α₂₂ = 145, να βρείτε τον α₁₈.
5.	Ποιος όρος της αριθμητικής προόδου με α₁ = 2 και ω = 5 ισούται με 97; Ποιος όρος της αριθμητικής προόδου με α₁ = 80 και ω = –3 ισούται με –97;
6.	Να βρείτε τον αριθμητικό μέσο των 10 και –40 Να βρείτε για ποια τιμή του x ο αριθμητικός μέσος των 5x+1 και 11 είναι ο 3x–2.
7.	Αν δυο αριθμοί διαφέρουν κατά 10 και ο αριθμητικός τους μέσος είναι ο 25, να βρείτε τους δυο αυτούς αριθμούς.
8.	Να βρείτε το άθροισμα των πρώτων 40 όρων των αριθμητικών προόδων:
	i)7,9,11,... ii) 0, 2, 4,.... iii) 6, 10, 14,... iv)–7,–2,+3,...
9.	Να βρείτε το άθροισμα των πρώτων 80 όρων των αριθμητικών προόδων:

10.	Να υπολογίσετε τα αθροίσματα:
	i) 1+5+9 + .. + 197 ii) 9+12+15+ ... + 90 iii) –7–10–13–...–109
11.	Πόσους πρώτους όρους πρέπει να πάρουμε από καθεμιά από τις παρακάτω αριθμητικές προόδους για να έχουν άθροισμα 180;
	i) 4, 8, 12,... ii) 5, 10, 15,...
12.	Μια στέγη σχήματος τραπεζίου έχει 15 σειρές κεραμίδια. Η πρώτη σειρά έχει 53 κεραμίδια και κάθε επόμενη σειρά έχει δυο κεραμίδια λιγότερα. Πόσα κεραμίδια έχει η 15η σειρά και πόσα κεραμίδια έχει συνολικά η στέγη;

B' ΟΜΑΔΑΣ

1.	Ο ν–ος όρος μιας ακολουθίας είναι α_ν = 12–4ν. Να δείξετε ότι η ακολουθία αυτή είναι αριθμητική πρόοδος και να γράψετε τον πρώτο όρο της α₁ και τη διαφορά της ω.
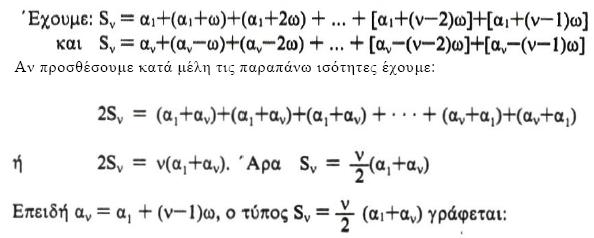
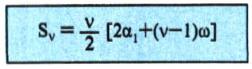
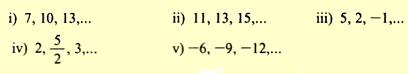
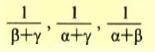2.	Αν οι α, β, γ είναι θετικοί αριθμοί και οι α², β², γ² είναι διαδοχικοί όροι αριθμητικής προόδου, να δείξετε ότι και οι αριθμοί είναι επίσης διαδοχικοί όροι αριθμητικής προόδου.
3.	Αν οι α1, β1 γ1 καθώς και οι α₂, β₂, γ₂ είναι διαδοχικοί όροι μιας αριθμητικής προόδου να δείξετε ότι το σύστημα έχει ως μια λύση το ζεύγος (–1, 2).
4.	Να βρείτε το άθροισμα: ί) των πρώτων 200 περιττών αριθμών, ii) των πρώτων 300 θετικών άρτιων iii) όλων των περιττών αριθμών μεταξύ 16 και 380.
5.	Να βρείτε το άθροισμα: των πολλαπλασίων του 5 μεταξύ 1 και 199, των πολλαπλασίων του 3 μεταξύ 10 και 200
6.	Να βρείτε το άθροισμα: των πρώτων 30 όρων της ακολουθίας α_ν = 5ν–4, των πρώτων 40 όρων της ακολουθίας α_ν = –5ν–3.
7.	Να βρείτε το άθροισμα των ακεραίων από 1 μέχρι 200 που δεν είναι πολλαπλάσια του 4 ή του 9.
8.	Να βρείτε το ελάχιστο πλήθος πρώτων όρων της αριθμητικής προόδου 1, 3, 5, 7,... που απαιτούνται, ώστε το άθροισμα του να ξεπερνάει το 4000.
9.	i) Είναι γνωστό ότι, για κάθε vN^*, το άθροισμα των πρώτων ν όρων μιας ακολουθίας (α_ν) είναι Να δείξετε ότι η (α_ν) είναι αριθμητική πρόοδος και να γράψετε τους α₁ , και ω. ii) Ομοίως, αν είναι
10.	Να συμπληρώσετε το διπλανό πίνακα, στον οποίο τα α₁, ω, ν, α_ν και S_ν ανήκουν σε κάθε γραμμή στην ίδια αριθμητική πρόοδο

11.	Ένα ρολόι χτυπάει τις ακέραιες ώρες. Πόσα χτυπήματα ακούγονται σε ένα 24/ωρο;
12.	Ένα στάδιο έχει 33 σειρές καθισμάτων. Στην κάτω–κάτω σειρά βρίσκονται 800 θέσεις και στην πάνωπάνω σειρά βρίσκονται 4160 θέσεις. Το πλήθος των θέσεων αυξάνει από σειρά σε σειρά κατά τον ίδιο πάντα αριθμό θέσεων. Να βρείτε πόσες θέσεις έχει συνολικά το στάδιο και πόσες θέσεις έχει η μεσαία σειρά.
13.	Να βρείτε τέσσερις ακέραιους αριθμούς που αποτελούν διαδοχικούς όρους μιας αριθμητικής προόδου, αν το άθροισμα τους είναι 32 και το γινόμενο τους είναι 1680.
14.	Μεταξύ των αριθμών 3 και 80 θέλουμε να βρούμε άλλους 10 αριθμούς που όλοι μαζί να είναι διαδοχικοί όροι μιας αριθμητικής προόδου. Να βρεθούν οι αριθμοί αυτοί. [Τέτοια προβλήματα λέγονται προβλήματα παρεμβολής όρων].
15.	Να υπολογίσετε το άθροισμα:
16.	Ένας αγρότης, για να κάνει μία γεώτρηση στο κτήμα του, συμφώνησε τα εξής με τον ιδιοκτήτη του γεωτρύπανου: Το 1 μέτρο θα κοστίσει 20 ευρώ και αυξανομένου του βάθους, θα αυξάνεται και η τιμή κάθε μέτρου κατά 5 ευρώ. Ο αγρότης διαθέτει 4700 ευρώ. Σε πόσο βάθος μπορεί να πάει η γεώτρηση στο κτήμα του;