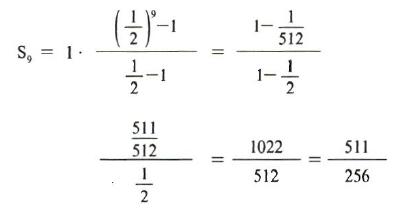| 1. |
Ο ν όρος μιας ακολουθίας είναι
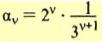 . Να δείξετε ότι η ακολουθία αυτή είναι γεωμετρική πρόοδος και να γράψετε τους α1 και λ. . Να δείξετε ότι η ακολουθία αυτή είναι γεωμετρική πρόοδος και να γράψετε τους α1 και λ. |
| 2. |
i) Αν ισχύει
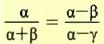 να δείξετε ότι οι α, β, γ είναι διαδοχικοί όροι μιας γεωμετρικής προόδου. να δείξετε ότι οι α, β, γ είναι διαδοχικοί όροι μιας γεωμετρικής προόδου. |
| |
ii) Αν οι α, β, γ είναι διαδοχικοί όροι μιας γεωμετρικής προόδου, να δείξετε ότι
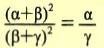 |
| 3. |
i) Αν οι α, β, γ είναι διαδοχικοί όροι μιας γεωμετρικής προόδου, να δείξετε ότι α2+β2+γ2=(α+β+γ)(α–β+γ) |
| |
ii) Αν οι α, β, γ, δ είναι διαδοχικοί όροι μιας γεωμετρικής προόδου να δείξετε ότι (α–γ)2+(β–γ)2+(β–δ)2=(α–δ)2 |
| 4. |
Για ποια τιμή του ν οι αριθμοί
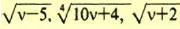 είναι διαδοχικοί όροι γεωμετρικής προόδου; είναι διαδοχικοί όροι γεωμετρικής προόδου; |
| 5. |
Να δείξετε ότι: |
| |
i) τα τετράγωνα των όρων μιας γεωμετρικής προόδου σχηματίζουν επίσης γεωμετρική πρόοδο
ii) Αν υψώσουμε κάθε όρο μιας γεωμετρικής προόδου στην k, τότε προκύπτει πάλι γεωμετρική πρόοδος. |
| 6. |
Να βρείτε τη γεωμετρική πρόοδο, της οποίας: |
| |
i) ο 4ος όρος είναι 24 και το άθροισμα των τριών πρώτων όρων της είναι 21,
ii) το άθροισμα των δυο πρώτων όρων της είναι
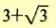 και το άθροισμα των τεσσάρων πρώτων όρων της είναι και το άθροισμα των τεσσάρων πρώτων όρων της είναι
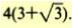 |
| 7. |
Να βρείτε το άθροισμα των πρώτων δέκα όρων της γεωμετρικής προόδου, στην οποία είναι α2+α6 =34 και α3+α7=68 |
| 8. |
i) Να βρείτε το άθροισμα 1+α+α2+..+αν–1 |
| |
ii) Να υπολογίσετε το γινόμενο (1–α)(1+α+α2+...+αν–1)
iii) Να δείξετε ότι xν–yν=(x–y)(xν–1+xν–2y+..+yν–1) |
| 9. |
Να υπολογίσετε το γινόμενο των πρώτων ν όρων της γεωμετρικής προόδου 2, 4, 8,... |
| 10. |
Αν το άθροισμα των πρώτων τριών όρων μιας γεωμετρικής προόδου είναι –13 και το γινόμενο τους είναι
–27, να βρείτε τους όρους αυτούς. |
| 11. |
i) Είναι γνωστό ότι, για κάθε ν N*, το άθροισμα των πρώτων ν όρων μιας ακολουθίας (αν) είναι Sν = 2ν–1. Να δείξετε ότι η (αν) είναι γεωμετρική πρόοδος και να γράψετε τους α1 και λ. N*, το άθροισμα των πρώτων ν όρων μιας ακολουθίας (αν) είναι Sν = 2ν–1. Να δείξετε ότι η (αν) είναι γεωμετρική πρόοδος και να γράψετε τους α1 και λ. |
| |
ii) Ομοίως, αν Sν = 3ν–1 iii) Ομοίως, αν Sν = 3(2ν–1) |
| 12. |
Να αποδείξετε ότι
 |
| 13. |
Ο πληθυσμός μιας χώρας είναι 90 εκατομμύρια και παρουσιάζει ετήσια αύξηση 2%. Αν αν είναι ο πληθυσμός της χώρας ύστερα από ν χρόνια, να βρείτε έναν αναδρομικό τύπο, καθώς και το γενικό όρο της ακολουθίας (αν). |
| |
– Ποιός θα είναι ο πληθυσμός της χώρας ύστερα από 10 χρόνια; [Χρησιμοποιήστε υπολογιστή τσέπης]. |
| 14. |
Η ένταση του φωτός μειώνεται κατά 10%, όταν αυτό διέρχεται από ένα φίλτρο. Αν Ιν είναι η ένταση του φωτός, αφού διέλθει διαδοχικά μέσα από ν τέτοια φίλτρα, να βρείτε έναν αναδρομικό τύπο, καθώς και το γενικό όρο της ακολουθίας ( Ιν ). |
| |
– Ποια θα είναι η ένταση του φωτός, αν διέλθει μέσα από 10 τέτοια φίλτρα και η αρχική ένταση είναι Ι0 ; [Χρησιμοποιήστε υπολογιστή τσέπης]. |
| 15. |
Σε ένα όργανο μουσικής ο τόνος C' έχει συχνότητα 261 Hz και η οκτάβα του C" έχει διπλάσια συχνότητα. Ανάμεσα στους C' και C" υπάρχουν 11 επιπλέον τόνοι, των οποίων οι συχνότητες σχηματίζουν με τις συχνότητες των C' και C" 13 διαδοχικούς όρους γεωμετρικής προόδου. Να υπολογίσετε: |
| |
i) το λόγο της προόδου, ii) τη συχνότητα του πέμπτου τόνου. |
| 16. |
Το ψυγείο ενός φορτηγού περιέχει 40 It νερό. Αδειάζουμε 4 lt νερό και το αντικαθιστούμε με αντιπυκτικό. Ύστερα αδειάζουμε 4 It του μείγματος και το αντικαθιστούμε με αντιπυκτικό κ.ο.κ. Αν Dν είναι η ποσότητα του νερού στο ψυγείο, αφού εφαρμοσθεί η διαδικασία ν φορές, να βρείτε: |
| |
i) Έναν αναδρομικό τύπο της ακολουθίας (Dν).
ii) Την ποσότητα του αντιπυκτικού στο ψυγείο, αφού εφαρμοσθεί η διαδικασία 7 φορές. [Χρησιμοποιήστε υπολογιστή τσέπης]. |
| 17. |
Λέγεται ότι ο εφευρέτης του σκακιού παρακλήθηκε από έναν Ινδό βασιλιά να ζητήσει όποια αμοιβή ήθελε για τη σπουδαία ιδέα του. Ο εφευρέτης ζήτησε να πάρει το ρύζι που θα μαζευόταν ως εξής: Στο 1ο τετραγωνάκι του σκακιού να έβαζε κάποιος έναν κόκκο ρυζιού, στο 2ο τετραγωνάκι 2 κόκκους, στο 3ο τετραγωνάκι 4 κόκκους, στο 5ο τετραγωνάκι 8 κόκκους κτλ.
Να βρείτε πόσοι τόνοι θα ήταν η ποσότητα αυτή του ρυζιού, αν 1 Kg ρυζιού έχει 20000 κόκκους. |
| |
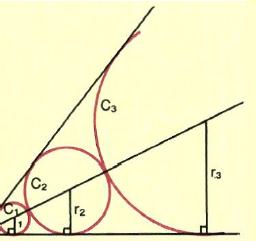
Στο εσωτερικό μιας γωνίας 60° βρίσκονται κύκλοι Ci, C2, C3,... που εφάπτονται διαδοχικά και έχουν τις πλευρές της γωνίας ως κοινές εφαπτόμενες
Αν rv είναι η ακτίνα του κύκλου Cν και η ακτίνα του C, είναι 1 να βρείτε:
i) Έναν αναδρομικό τύπο και το ν° όρο της ακολουθίας (rν)
ii) Την ακτίνα του 8 κύκλου
iii) Το άθροισμα των εμβαδών των 5 πρώτων κύκλων. |
 |
|
![]()
![]() .Δηλαδή για την ακολουθία αυτή ισχύει:
.Δηλαδή για την ακολουθία αυτή ισχύει: 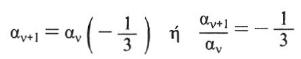
![]()
![]() N*. Επομένως, η ακολουθία (αν) είναι γεωμετρική πρόοδος με λόγο λ, αν και μόνο αν ισχύει:
N*. Επομένως, η ακολουθία (αν) είναι γεωμετρική πρόοδος με λόγο λ, αν και μόνο αν ισχύει: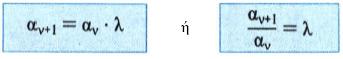
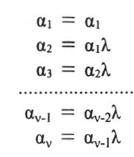

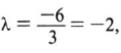 ο
ν–ος όρος της είναι αν = 3 · (–2)ν–1. Επομένως ο 5ος όρος της είναι
ο
ν–ος όρος της είναι αν = 3 · (–2)ν–1. Επομένως ο 5ος όρος της είναι
![]() ο δέκατος όρος της είναι
ο δέκατος όρος της είναι
![]()
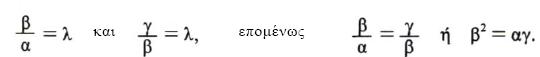
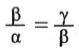 που σημαίνει ότι οι α, β, γ είναι διαδοχικοί όροι μιας γεωμετρικής προόδου. Ο θετικός αριθμός
που σημαίνει ότι οι α, β, γ είναι διαδοχικοί όροι μιας γεωμετρικής προόδου. Ο θετικός αριθμός
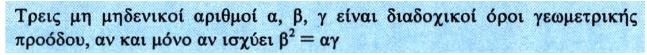
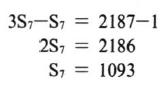


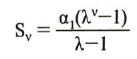
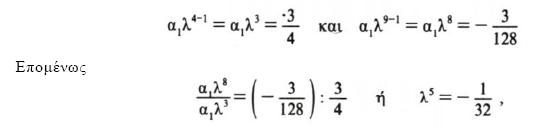
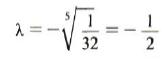

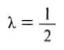
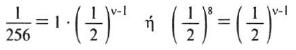 και επομένως ν– 1 = 8 ή ν=9.
και επομένως ν– 1 = 8 ή ν=9.