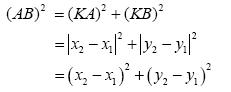6.2 ΓΡΑΦΙΚΗ ΠΑΡΑΣΤΑΣΗ ΣΥΝΑΡΤΗΣΗΣ

Καρτεσιανές συντεταγμένες

Η παράσταση ενός σημείου του επιπέδου με ένα διατεταγμένο ζεύγος πραγματικών αριθμών, βοήθησε στην επίλυση γεωμετρικών προβλημάτων με αλγεβρικές μεθόδους. Η παράσταση αυτή, όπως μάθαμε σε προηγούμενες τάξεις, γίνεται ως εξής:

Πάνω σε ένα επίπεδο σχεδιάζουμε δύο κάθετους άξονες x'x και y'y με κοινή αρχή ένα σημείο Ο. Από αυτούς ο οριζόντιος x'x λέγεται άξονας των τετμημένων ή άξονας των x, ενώ ο κατακόρυφος y'y άξονας των τεταγμένων ή άξονας των y.

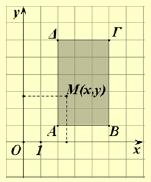
Όπως είναι γνωστό, σε κάθε σημείο Μ του επιπέδου των αξόνων μπορούμε να αντιστοιχίσουμε ένα διατεταγμένο ζεύγος (α, β) πραγματικών αριθμών και αντιστρόφως, σε κάθε διατεταγμένο ζεύγος (α, β) πραγματικών αριθμών, μπορούμε να αντιστοιχίσουμε ένα μοναδικό σημείο Μ του επιπέδου, όπως φαίνεται στο σχήμα:

Οι αριθμοί α, β λέγονται συντεταγμένες του Μ. Ειδικότερα ο α λέγεται τετμημένη και ο β τεταγμένη του σημείου Μ. Το σημείο Μ που έχει συντεταγμένες α και β συμβολίζεται με Μ(α, β) ή, απλά, με (α, β).

Επειδή η ιδέα της χρησιμοποίησης ζευγών για την παράσταση σημείων του επιπέδου ανήκει στον Καρτέσιο, το παραπάνω ζεύγος των αξόνων το λέμε καρτεσιανό σύστημα συντεταγμένων στο επίπεδο και το συμβολίζουμε Οxy , ενώ το επίπεδο στο οποίο ορίστηκε το σύστημα αυτό το λέμε καρτεσιανό επίπεδο. Αν επιπλέον οι μονάδες των αξόνων έχουν το ίδιο μήκος, το σύστημα Οxy λέγεται ορθοκανονικό.

ΣΗΜΕΙΩΣΗ:

Στα επόμενα, εκτός αν αναφέρεται διαφορετικά, όταν λέμε καρτεσιανό σύστημα συντεταγμένων, θα εννο–ούμε ορθοκανονικό καρτεσιανό σύστημα συντεταγμένων.

Ας θεωρήσουμε τώρα ένα σύστημα Oxy συντεταγμένων στο επίπεδο. Τότε:

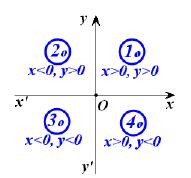
• Τα σημεία του άξονα x'x και μόνο αυτά έχουν τεταγμένη ίση με το μηδέν, ενώ τα σημεία του άξονα y'y και μόνο αυτά έχουν τετμημένη ίση με το μηδέν

Οι άξονες χωρίζουν το επίπεδο σε τέσσερα τεταρτημόρια, που είναι τα εσωτερικά των γωνιών και ονομάζεται 1ο, 2ο, 3ο και 4ο, τεταρτημόριο, αντιστοίχως. Τα πρόσημα των συντεταγμένων των σημείων τους φαίνονται στο παρακάτω σχήμα.

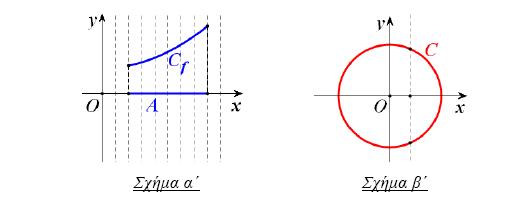
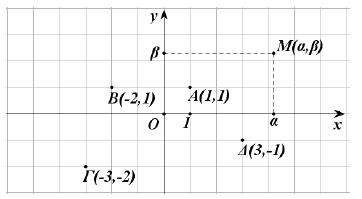
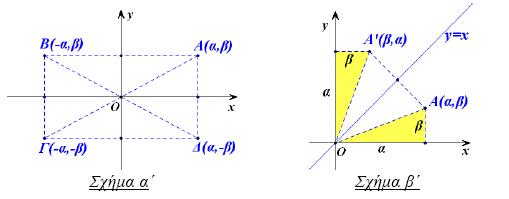
• Αν Α (α, β) είναι ένα σημείο του καρτεσιανού επιπέδου, με τη βοήθεια της συμμετρίας ως προς άξονα και ως προς κέντρο, διαπιστώνουμε ότι:

• Το συμμετρικό του ως προς τον άξονα x'x είναι το σημείο Δ (α,–β), που έχει ίδια τετμημένη και αντίθετη τεταγμένη (Σχ. α').

• Το συμμετρικό του ως προς τον άξονα y'y είναι το σημείο Β(–α,β), που έχει ίδια τεταγμένη και αντίθετη τετμημένη (Σχ. α').

• Το συμμετρικό του ως προς την αρχή των αξόνων είναι το σημείο Γ (–α,–β), που έχει αντίθετες συντεταγμένες (Σχ. α').

• Το συμμετρικό του ως προς τη διχοτόμο της 1^ης και 3^ης γωνίας των αξόνων είναι το σημείο Α'(β,α) που έχει τετμημένη την τεταγμένη του Α και τεταγμένη την τετμημένη του Α (Σχ. β').

Απόσταση σημείων

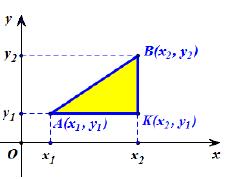
Έστω Oxy ένα σύστημα συντεταγμένων στο επίπεδο και Α(x₁,y₁) και Β(x₂,y₂) δύο σημεία αυτού. Θα δείξουμε ότι οι απόστασή τους δίνεται από τον τύπο:

ΑΠΟΔΕΙΞΗ:

Ο παραπάνω τύπος ισχύει και στην περίπτωση που η ΑΒ είναι παράλληλη με τον άξονα x'x (Σχήμα γ') ή παράλληλη με τον άξονα y'y (Σχήμα δ').

Για παράδειγμα, αν Α(3,1), Β(3,5) και Γ (–1,1) είναι οι κορυφές ενός τριγώνου ΑΒΓ, τότε θα είναι:

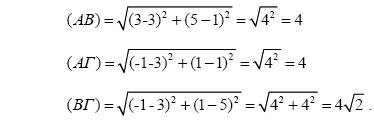
Αφού, λοιπόν, είναι (ΑΒ) = (ΑΓ), το τρίγωνο ΑΒΓ είναι ισοσκελές και επειδή επιπλέον ισχύει (ΑΒ)² + (ΑΓ)² = 32 = (ΒΓ)², το τρίγωνο ΑΒΓ είναι και ορθογώνιο .

ΕΦΑΡΜΟΓΗ

Επομένως το σημείο Μ (x,y) ανήκει στο κύκλο C (Ο,ρ), αν και μόνο αν οι συντεταγμένες του ικανοποιούν την εξίσωση

Η εξίσωση (1), που ικανοποιείται από τις συντεταγμένες των σημείων του κύκλου C (Ο, ρ) και μόνο από αυτές, λέγεται εξίσωση του κύκλου με κέντρο Ο και ακτίνα ρ.

Για παράδειγμα, η εξίσωση του κύκλου με κέντρο Ο και ακτίνα ρ = 1 είναι η x² + y² = 1. Ο κύκλος αυτός λέγεται και μοναδιαίος κύκλος.

Γραφική παρασταση συνάρτησης

Έστω ƒ μια συνάρτηση με πεδίο ορισμού Α και Oxy ένα σύστημα συντεταγμένων στο επίπεδο. Το σύνολο των σημείων M (x, y) για τα οποία ισχύει y = ƒ(x), δηλαδή το σύνολο των σημείων M (x, ƒ(x)), xA, λέγεται γραφική παράσταση της ƒ και συμβολίζεται συνήθως με Cƒ . Η εξίσωση, λοιπόν, y = ƒ(x) επαληθεύεται από τα σημεία της Cƒ και μόνο από αυτά. Επομένως, η y = ƒ(x) είναι η εξίσωση της γραφικής παράστασης της ƒ. Για το λόγο αυτό, τη γραφική παράσταση Cƒ της ƒ τη συμβολίζουμε, πολλές φορές, απλά με την εξίσωσή της, δηλαδή με y = ƒ(x).

Επειδή κάθε x A αντιστοιχίζεται σε ένα μόνο yR , δεν υπάρχουν σημεία της γραφικής παράστασης της ƒ με την ίδια τετμημένη. Αυτό σημαίνει ότι κάθε κατακόρυφη ευθεία έχει με τη γραφική παράσταση της ƒ το πολύ ένα κοινό σημείο (Σχ. α'). Έτσι, ο κύκλος δεν αποτελεί γραφική παράσταση συνάρτησης (Σχ. β').

ΕΦΑΡΜΟΓΗ

ΛΥΣΗ

i) Είναι:

ƒ(–3) = 2, ƒ(–2) = 0, ƒ(–1) = –1, ƒ(0 ) = –1, ƒ(1) = 0 και ƒ(2) = 2.

ii) Οι ρίζες της εξίσωσης ƒ(x) = 0 είναι οι τετμημένες των κοινών σημείων της γραφικής παράστασης της f και του άξονα x'x, δηλαδή οι αριθμοί x₁ = –2 και x₂ = 1.

Οι ρίζες της εξίσωσης ƒ(x) = 2 είναι οι τετμημένες των σημείων της γραφικής παράστασης της ƒ που έχουν τεταγμένη 2, δηλαδή οι αριθμοί x₁ = –3 και x₂ = 2 .

Οι ρίζες της εξίσωσης ƒ(x) = g(x) είναι οι τετμημένες των κοινών σημείων των γραφικών παραστά–σεων των συναρτήσεων ƒ και g , δηλαδή οι αριθμοί x₁ = –1, x₂ = 0 και x₃ = 2 .

iii) Οι λύσεις της ανίσωσης ƒ(x) > 0 είναι οι τετμημένες των σημείων της γραφικής παράστασης της ƒ που βρίσκονται πάνω από τον άξονα x'x, δηλαδή όλα τα x(–∞, –2) U (1, +∞).

Οι λύσεις της ανίσωσης ƒ(x) > g(x) είναι οι τετμημένες των σημείων της γραφικής παράστασης της ƒ που βρίσκονται πάνω από τη γραφική παράσταση της g , δηλαδή όλα τα x(–∞, –1) U (0,2).

Ασκήσεις