6.3 Η ΣΥΝΑΡΤΗΣΗ ƒ(x) = αx + β

Συντελεστής διεύθυνσης ευθείας

Έστω Oxy ένα σύστημα συντεταγμένων στο επίπεδο και ε μια ευθεία που τέμνει τον άξονα x'x στο σημείο Α.

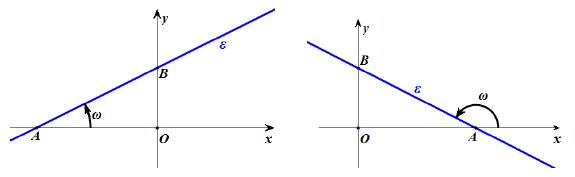
Τη γωνία ω που διαγράφει η ημιευθεία Αx , όταν στραφεί γύρω από το Α κατά τη θετική φορά⁽¹⁾ μέχρι να πέσει πάνω στην ευθεία ε, τη λέμε γωνία που σχηματίζει η ε με τον άξονα x'x . Αν η ευθεία ε είναι παράλληλη προς τον άξονα x 'x ή συμπίπτει με αυτόν, τότε λέμε ότι η ευθεία ε σχηματίζει με τον άξονα x 'x γωνία ω = 0°. Σε κάθε περίπτωση για τη γωνία ω ισχύει

0° ≤ ω ≤ 180°.

Ως συντελεστή διεύθυνσης ή ως κλίση μιας ευθείας ε ορίζουμε την εφαπτομένη της γωνίας ω που σχηματίζει η ε με τον άξονα x'x. Ο συντελεστής διεύθυνσης μιας ευθείας ε συμβολίζεται συνήθως με λ_ε. ή απλά με λ. Είναι φανερό ότι ο συντελεστής διεύθυνσης της ευθείας ε είναι θετικός, αν η γωνία ω είναι οξεία, αρνητικός, αν η γωνία ω είναι αμβλεία και μηδέν, αν η γωνία ω είναι μηδέν. Στην περίπτωση που η γωνία ω είναι ίση με 90°, δηλαδή όταν η ευθεία ε είναι κάθετη στον άξονα x'x, δεν ορίζουμε συντελεστή διεύθυνσης για την ε.

⁽¹⁾ Ως θετική φορά περιστροφής εννοούμε τη φορά κατά την οποία πρέπει να περιστραφεί ο ημιάξονας Οx για να συμπέσει με τον ημιάξονα Oy, αφού προηγουμένως διαγράψει γωνία 90°

Γραφική παράσταση της συνάρτησης ƒ(x) = αx + β

Ας θεωρήσουμε τη συνάρτηση ƒ(x) = 0,5x + 1. Όπως πρακτικά διαπιστώσαμε στο Γυμνάσιο, η γραφική παράσταση της ƒ είναι ευθεία γραμμή με εξίσωση y = 0,5x + 1 (Σχήμα).

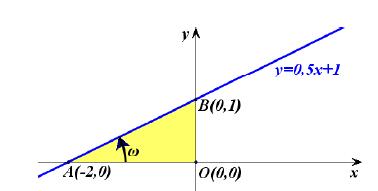
Η ευθεία αυτή:

• Τέμνει τον άξονα x'x στο σημείο Α(–2,0), αφού για y = 0 βρίσκουμε x = –2, και τον άξονα y'y στο σημείο Β(0,1), αφού για x = 0 βρίσκουμε y = 1 και

• Έχει κλίση:

Παρατηρούμε, δηλαδή, ότι η κλίση λ της ευθείας y = 0,5x + 1 είναι ίση με το συντελεστή του x.

Γενικά, όπως θα αποδείξουμε στην Β' Λυκείου, η γραφική παράσταση της συνάρτησης ƒ(x) = αx + β είναι μία ευθεία, με εξίσωση y = αx + β, η οποία τέμνει τον άξονα των y στο σημείο Β(0,β) και έχει κλίση λ = α . Είναι φανερό ότι:

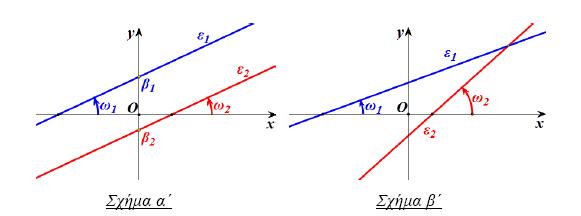
• αν α > 0 , τότε 0° < ω < 90°
• αν α < 0, τότε 90° < ω < 180°
• αν α = 0 , τότε ω = 0°.

Στην περίπτωση που είναι α = 0 , η συνάρτηση παίρνει την μορφή ƒ(x) = β και λέγεται σταθερή συνάρτηση, διότι η τιμή της είναι η ίδια για κάθε xR.

Ας θεωρήσουμε τώρα δύο τυχαία σημεία A(x₁,y₁) και B(x₂,y₂) της ευθείας y = α – x + β .

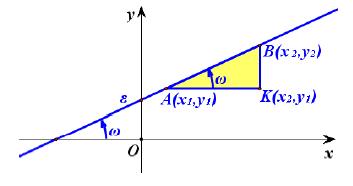
Τότε θα ισχύει:

y₁ = αx₁ + β και y₂ = αx₂ + β,

οπότε θα έχουμε:

y₂ – y₁ = (αx₂ + β) – (αx₁ + β) = α(x₂ – x₁).

Επομένως θα είναι:

Για παράδειγμα, η ευθεία που διέρχεται από τα σημεία A(–1,3) και B(3,6) έχει κλίση 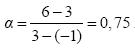. Επομένως, η ευθεία αυτή σχηματίζει με τον άξονα x'x γωνία ω με εφω = 0,75, οπότε θα είναι ω = 36,87°.

Η συνάρτηση ƒ(x) = αx

Αν β = 0, τότε η ƒ παίρνει τη μορφή ƒ(x) = αx , οπότε η γραφική της παράσταση είναι η ευθεία y = αx και περνάει από την αρχή των αξόνων. Ειδικότερα:

Σχετικές θέσεις δύο ευθειών

Ας θεωρήσουμε δύο ευθείες ε₁ και ε₂ με εξισώσεις y = α₁x + β₁ και y = α₂x + β₂ αντιστοίχως και ας υποθέσουμε ότι οι ευθείες αυτές σχηματίζουν με τον άξονα x'x γωνίες ω₁ και ω₂ αντιστοίχως.

• Αν α₁ = α₂, τότε εφω₁ = εφω₂, οπότε ω₁ = ω₂ και άρα οι ευθείες ε₁ και ε₂ είναι παράλληλες ή συμπίπτουν. Ειδικότερα :

• Αν α₁ = α₂ και β₁ ≠ β₂, τότε οι ευθείες είναι παράλληλες (Σχ. α'), ενώ

• Αν α₁ = α₂ και β₁ = β₂, τότε οι ευθείες ταυτίζονται.

• Αν α₁ ≠ α₂, τότε εφω₁ ≠ εφω₂, οπότε ω₁ ≠ ω₂ και άρα οι ευθείες ε₁ και ε₂ τέμνονται. (Σχ. β')

Σύμφωνα με τα παραπάνω συμπεράσματα:

Η συνάρτηση ƒ(x) = |x|

Σύμφωνα με τον ορισμό της απόλυτης τιμής έχουμε:

ΕΦΑΡΜΟΓΗ

ΛΥΣΗ

Για να δείξουμε τώρα ότι το σημείο Γ ανήκει στην ευθεία ΑΒ, αρκεί να δείξουμε ότι το ζεύγος (–2,2) των συντεταγμένων του επαληθεύει την εξίσωση αυτής, δηλαδή αρκεί να δείξουμε ότι 2 = –0,5 · (–2) + 1, που ισχύει.

ii) Οι λύσεις της ανίσωσης ƒ(x) > –0,5 · x + 1 είναι οι τετμημένες των σημείων της γραφικής παράστασης της ƒ που βρίσκονται πάνω από την ευθεία με εξίσωση y = –0,5 · x + 1, δηλαδή πάνω από την ευθεία ΑΒ. Επομένως, η ανίσωση αυτή αληθεύει για x(–2,0) U (2, +∞).

Ασκήσεις

Α' ΟΜΑΔΑΣ
1.	Να βρείτε τη γωνία που σχηματίζει με τον άξονα x' x η ευθεία:
2.	Να βρείτε την κλίση της ευθείας που διέρχεται από τα σημεία:
3.	Να βρείτε την εξίσωση της ευθείας η οποία: Έχει κλίση α = –1 και τέμνει τον άξονα y'y στο σημείο B(0,2). Σχηματίζει με τον άξονα x'x γωνία ω = 45° και τέμνει τον άξονα y'y στο σημείο B(0,1). Είναι παράλληλη με την ευθεία y = 2x – 3 και διέρχεται από το σημείο A (1,1).
4.	Να βρείτε την εξίσωση της ευθείας που διέρχεται από τα σημεία:
5.	Να αποδείξετε ότι η εξίσωση της ευθείας που παριστάνει τη σχέση μεταξύ της θερμοκρασίας C σε βαθμούς Celsius και της θερμοκρασίας F σε βαθμούς Fahrenheit είναι η Γνωρίζουμε ότι το νερό παγώνει σε 0oC ή 32°F και βράζει σε 100°C ή 212°F. Υπάρχει θερμοκρασία που να εκφράζεται και στις δύο κλίμακες με τον ίδιο αριθμό;
6.	Να παραστήσετε γραφικά τη συνάρτηση:
7.	Στο παρακάτω σχήμα δίνονται η γραφική παράσταση μιας συνάρτησης ƒ που είναι ορισμένη σε όλο το R και η ευθεία y = x. Να λύσετε γραφικά: i) Τις εξισώσεις: ƒ(x) = 1 και ƒ(x) = x . ii) Τις ανισώσεις: ƒ(x) < 1 και ƒ(x) ≥ x .
8.	i) Στο ίδιο σύστημα συντεταγμένων να χαράξετε τις γραφικές παραστάσεις των συναρτήσεων ƒ(x) = |x| και g(x) = 1 και με τη βοήθεια αυτών να λύσετε τις ανισώσεις: |x| ≤ 1 και |x| > 1. ii) Να επιβεβαιώσετε αλγεβρικά τις απαντήσεις σας στο προηγούμενο ερώτημα.