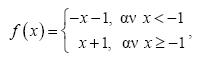Βασικές Έννοιες των Συναρτήσεων

6.4 ΚΑΤΑΚΟΡΥΦΗ – ΟΡΙΖΟΝΤΙΑ ΜΕΤΑΤΟΠΙΣΗ ΚΑΜΠΥΛΗΣ

Κατακόρυφη μετατόπιση καμπύλης

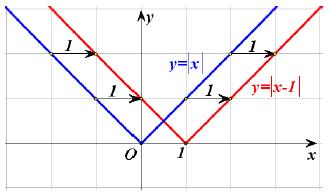
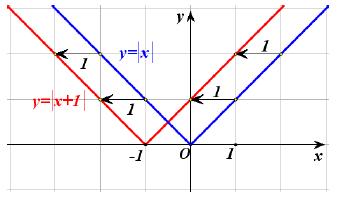
α) Ας θεωρήσουμε τη συνάρτηση ƒ(x) = |x| + 1. Επειδή

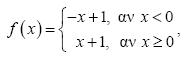
η γραφική παράσταση της συνάρτησης ƒ(x) = |x| + 1, θα αποτελείται από τις ημιευθείες

y = –x + 1, με x ≤ 0 και
y = x + 1, με x ≥ 0,

που έχουν αρχή το σημείο 1 του άξονα y' y και είναι παράλληλες με τις διχοτόμους των γωνιών και από τις οποίες, όπως είναι γνωστό, αποτελείται η γραφική παράσταση της φ(x) = |x| (Σχήμα).

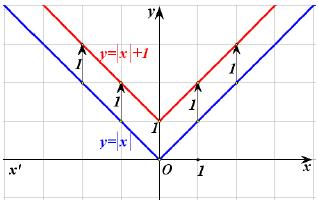Επομένως, αν μετατοπίσουμε τη γραφική παράσταση της φ(x) = |x| κατακόρυφα⁽¹⁾ και προς τα πάνω κατά 1 μονάδα, τότε αυτή θα συμπέσει με τη γραφική παράσταση της ƒ(x) = |x| +1. Αυτό, άλλωστε, ήταν αναμενόμενο, αφού ισχύει:

ƒ(x) = φ(x) + 1, για κάθε xR,

που σημαίνει ότι για κάθε xR το ƒ(x) είναι κατά 1 μονάδα μεγαλύτερο του φ(x).

Γενικά:

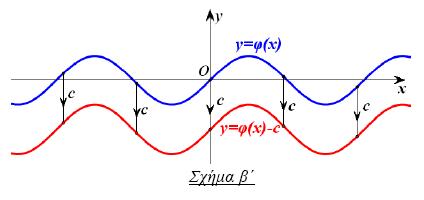
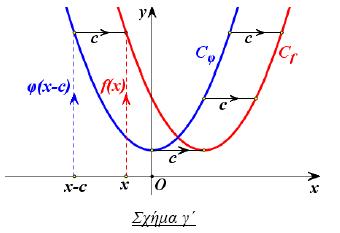
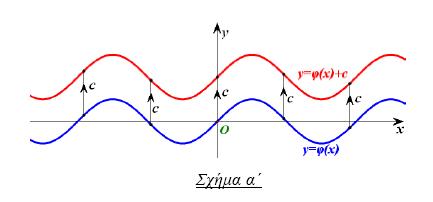
Η γραφική παράσταση της συνάρτησης ƒ , με:

ƒ(x) = φ(x) + c, όπου c > 0,

προκύπτει από μια κατακόρυφη μετατόπιση της γραφικής παράστασης της φ κατά c μονάδες προς τα πάνω (Σχήμα α')

⁽¹⁾ Δηλαδή παράλληλα με τον άξονα y'y

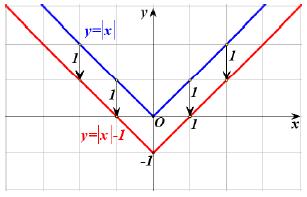
β) Ας θεωρήσουμε τη συνάρτηση ƒ(x) = |x| – 1. Επειδή

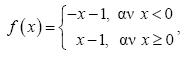
η γραφική παράσταση της ƒ(x) = |x| –1, θα αποτελείται από τις ημιευθείες

y = –x – 1, με x < 0 και
y = x – 1, με x > 0,

που έχουν αρχή το σημείο –1 του άξονα y' y και είναι παράλληλες με τις διχοτόμους των γωνιών και από τις οποίες αποτελείται η γραφική παράσταση της φ(x) = |x| (Σχήμα).

Επομένως, αν μετατοπίσουμε τη γραφική παράσταση της φ(x) = |x| κατακόρυφα και προς τα κάτω κατά 1 μονάδα, τότε αυτή θα συμπέσει με τη γραφική παράσταση της ƒ(x) = |x| – 1. Αυτό, άλλωστε, ήταν αναμενόμενο, αφού ισχύει :

ƒ(x) = φ(x) – 1, για κάθε xR,

που σημαίνει ότι για κάθε xR το ƒ(x) είναι κατά 1 μονάδα μικρότερο του φ(x).

Γενικά:

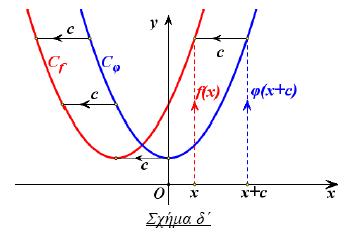
Η γραφική παράσταση της συνάρτησης ƒ , με:

ƒ(x) = φ(x) – c, όπου c > 0 ,

προκύπτει από μια κατακόρυφη μετατόπιση της γραφικής παράστασης της φ κατά c μονάδες προς τα κάτω (Σχήμα β')

Οριζόντια μετατόπιση καμπύλης

α) Ας θεωρήσουμε τη συνάρτηση ƒ(x) = |x – 1|. Επειδή

η γραφική παράσταση της ƒ(x) = |x – 1|, θα αποτελείται από τις ημιευθείες

y = –x + 1, με x < 1 και
y = x – 1, με x > 1,

αρχή το σημείο 1 του άξονα x'x και είναι παράλληλες με τις διχοτόμους των γωνιών και από τις οποίες αποτελείται η γραφική παράσταση της φ(x) = |x| (Σχήμα).

Επομένως, αν μετατοπίσουμε τη γραφική παράσταση της φ(x) = |x| οριζόντια⁽²⁾ και προς τα δεξιά κατά 1 μονάδα, τότε αυτή θα συμπέσει με τη γραφική παράσταση της ƒ(x) = |x –1|. Αυτό, άλλωστε, ήταν αναμενόμενο, αφού ισχύει

ƒ(x) = φ(x – 1) , για κάθε xR

σημαίνει ότι η τιμή της ƒ(x) = |x –1| στη θέση x είναι ίδια με την τιμή της φ(x) = |x| στη θέση x – 1.

Γενικά:

Η γραφική παράσταση της συνάρτησης ƒ με:

ƒ(x) = φ(x – c), όπου c > 0,

προκύπτει από μια οριζόντια μετατόπιση της γραφικής παράστασης της φ κατά c μονάδες προς τα δεξιά (Σχήμα γ').

⁽²⁾ Δηλαδή παράλληλα με τον άξονα x'x .

Πράγματι επειδή ƒ(x) = φ(x – c), η τιμή της ƒ στη θέση x είναι ίδια με την τιμή της φ στη θέση x – c, που βρίσκεται c μονάδες αριστερότερα της θέσης x. Άρα, η γραφική παράσταση της ƒ θα βρίσκεται c μονάδες δεξιότερα της γραφικής παράστασης της φ (Σχήμα γ').

β) Ας θεωρήσουμε τη συνάρτηση ƒ(x) = |x + 1| . Επειδή

η γραφική παράσταση της ƒ(x) = |x + 1|, θα αποτελείται από τις ημιευθείες

y = –x – 1, με x < –1 και
y = x + 1, με x > –1,

που έχουν αρχή το σημείο –1 του άξονα x' x και είναι παράλληλες με τις διχοτόμους των γωνιών και από τις οποίες αποτελείται η γραφική παράσταση της φ(x) = |x| (Σχήμα).

Επομένως, αν μετατοπίσουμε τη γραφική παράσταση της φ(x) = |x| οριζόντια και προς τα αριστερά κατά 1 μονάδα, τότε αυτή θα συμπέσει με τη γραφική παράσταση της ƒ(x) = |x + 1|. Αυτό, άλλωστε, ήταν αναμενόμενο, αφού ισχύει

ƒ(x) = φ(x + 1) , για κάθε xR ,

που σημαίνει ότι η τιμή της ƒ(x) = |x + 1| στη θέση x είναι ίδια με την τιμή της φ(x) = |x| στη θέση x + 1.

Γενικά:

Η γραφική παράσταση της συνάρτησης ƒ, με:

ƒ(x) = φ(x + c), όπου c > 0,

προκύπτει από μια οριζόντια μετατόπιση της γραφικής παράστασης της φ κατά c μονάδες προς τα αριστερά (Σχήμα δ').

Πράγματι• επειδή ƒ(x) = φ(x + c), η τιμή της ƒ στη θέση x είναι ίδια με την τιμή της φ στη θέση x + c, που βρίσκεται c μονάδες δεξιότερα της θέσης x. Άρα, η γραφική παράστα–ση της ƒ θα βρίσκεται c μονάδες αριστερότερα της γραφικής παράστασης της φ (Σχήμα δ').

ΕΦΑΡΜΟΓΗ

Να παραστεί γραφικά η συνάρτηση ƒ(x) = |x + 3| + 2:

ΛΥΣΗ

Αρχικά χαράσσουμε την y = |x + 3|, που όπως είδαμε προκύπτει από μια οριζόντια μετατόπιση της y = |x| κατά 3 μονάδες προς τα αριστερά. Στη συνέχεια χαράσσουμε την y = |x + 3| + 2,που όπως είδαμε προκύπτει από μια κατακόρυφη μετατόπιση της γραφικής παράστασης της y = |x + 3| κατά 2 μονάδες προς τα πάνω.

Επομένως, η γραφική παράσταση της

ƒ(x) = |x + 3| + 2

προκύπτει από δύο διαδοχικές μετατοπίσεις της συνάρτησης y = |x|, μιας οριζόντιας κατά 3 μονάδες προς τα αριστερά και μιας κατακόρυφης κατά 2 μονάδες προς τα πάνω (Σχήμα).

ΣΗΜΕΙΩΣΗ:

Με ανάλογο τρόπο, δουλεύουμε για να παραστήσουμε γραφικά τις συναρτήσεις της μορφής:

ƒ(x) = φ(x ± c) ± d, με c, d > 0

Δηλαδή, αξιοποιούμε τόσο την οριζόντια όσο και την κατακόρυφη μετατόπιση καμπύλης.

Ασκήσεις

Α' ΟΜΑΔΑΣ
1.	Στο ίδιο σύστημα συντεταγμένων να παραστήσετε γραφικά τις συναρτήσεις: φ(x) = \|x\|, ƒ(x) = \|x\| + 2 και g(x) = \|x\| – 2.
2.	Ομοίως για τις συναρτήσεις φ(x) = \|x\|, h(x) = \|x + 2\| και g(x) = \|x – 2\|.
3.	Ομοίως για τις συναρτήσεις φ(x) = \|x\|, F(x) = \|x + 2\| + 1 και g(x) = \|x – 2\| – 1.
4.	Στο παρακάτω σχήμα δίνεται η γραφική παράσταση μιας συνάρτησης φ που αποτελείται από την διχοτόμο της δεύτερης γωνίας των αξόνων και από το ημικύκλιο που ανήκει στο 1ο τεταρτημόριο και έχει διάμετρο που ορίζουν τα σημεία O(0,0) και A(2,0). Στο ίδιο σύστημα συντεταγμένων να παραστήσετε γραφικά τις συναρτήσεις: i) ƒ(x) = φ(x) + 2 και g(x) = φ(x) – 2 ii) h(x) = φ(x + 3) και q(x) = φ(x – 3) iii) F(x) = φ(x + 3) + 2 και G(x) = φ(x – 3) – 2.
5.	Δίνεται η συνάρτηση φ(x) = 2x2 –1. Να βρείτε τον τύπο της συνάρτησης ƒ της οποίας η γραφική παράσταση προκύπτει από δύο διαδοχικές μετατοπίσεις της γραφικής παράστασης της φ: i) κατά 2 μονάδες προς τα δεξιά και κατά 1 μονάδα προς τα πάνω. ii) κατά 3 μονάδες προς τα δεξιά και κατά 2 μονάδες προς τα κάτω. iii) κατά 2 μονάδες προς τα αριστερά και κατά 1 μονάδες προς τα πάνω. iv) κατά 3 μονάδες προς τα αριστερά και κατά 2 μονάδες προς τα κάτω.