Βασικές Έννοιες των Συναρτήσεων

6.5 ΜΟΝΟΤΟΝΙΑ – ΑΚΡΟΤΑΤΑ – ΣΥΜΜΕΤΡΙΕΣ ΣΥΝΑΡΤΗΣΗΣ

Μονοτονία συνάρτησης

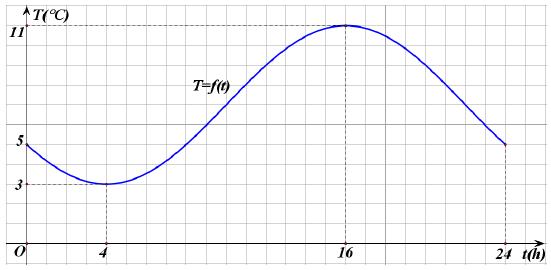
Στο παρακάτω σχήμα δίνεται η γραφική παράσταση της συνάρτησης T = ƒ(t) που εκφράζει τη θερμοκρασία Τ ενός τόπου συναρτήσει του χρόνου t κατά το χρονικό διάστημα από τα μεσάνυχτα μιας ημέρας (t = 0) μέχρι τα μεσάνυχτα της επόμενης μέρας (t = 24).

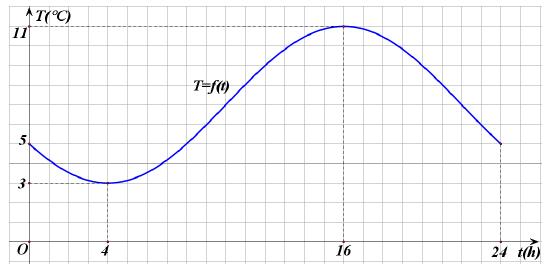
α) Παρατηρούμε ότι στο διάστημα [4,16] η γραφική παράσταση της θερμοκρασίας ανέρχεται.

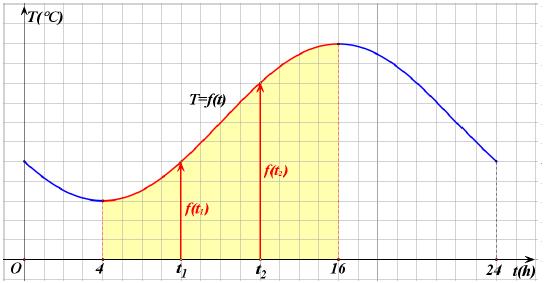
Αυτό σημαίνει ότι στο διάστημα αυτό, με την πάροδο του χρόνου, η θερμοκρασία αυξάνεται, δηλαδή για οποιαδήποτε t₁, t₂ [4,16] με t₁ < t₂ ισχύει:

ƒ(t₁) < ƒ(t₂)

Για το λόγο αυτό λέμε ότι η συνάρτηση T = ƒ(t) είναι γνησίως αύξουσα στο διάστημα [4,16].

Γενικά:

ΟΡΙΣΜΟΣ

Μια συνάρτηση ƒ λέγεται γνησίως αύξουσα σε ένα διάστημα Δ του πεδίου ορισμού της, όταν για οποιαδήποτε x₁, x₂ Δ με x₁ < x₂ ισχύει:

ƒ(x₁) < ƒ(x₂),

Για να δηλώσουμε ότι η συνάρτηση ƒ είναι γνησίως αύξουσα στο διάστημα Δ γράφουμε .

Για παράδειγμα, η συνάρτηση ƒ(x) = 2x – 3 είναι γνησίως αύξουσα στο R . Πράγματι έστω x₁,x₂R, με x₁ < x₂. Τότε έχουμε:

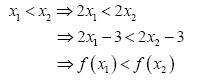
Γενικά:

Η συνάρτηση ƒ(x) = x + β, με α > 0 είναι γνησίως αύξουσα στο R.

β) Στο ίδιο σχήμα, παρατηρούμε επιπλέον ότι στο διάστημα [16,24] η γραφική παράσταση της θερμοκρασίας κατέρχεται.

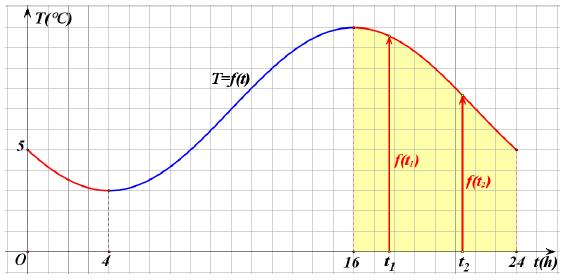
Αυτό σημαίνει ότι στο διάστημα αυτό, με την πάροδο του χρόνου, η θερμοκρασία μειώνεται, δηλαδή για οποιαδήποτε t₁, t₂[16,24] με t₁ < t₂ ισχύει:

ƒ(t₁) > ƒ(t₂)

Για το λόγο αυτό λέμε ότι η συνάρτηση T = ƒ(t) είναι γνησίως φθίνουσα στο διάστημα [16,24].

Γενικά:

ΟΡΙΣΜΟΣ

Μια συνάρτηση ƒ λέγεται γνησίως φθίνουσα σε ένα διάστημα Δ του πεδίου ορισμού της, όταν για οποιαδήποτε x₁, x₂Δ με x₁ < x₂ ισχύει:

ƒ(x₁) < ƒ(x₂),

Για να δηλώσουμε ότι η συνάρτηση είναι γνησίως φθίνουσα στο διάστημα Δ γράφουμε

Για παράδειγμα, η συνάρτηση ƒ(x) = –2x + 5 είναι γνησίως φθίνουσα στο R. Πράγματι• έστω x₁, x₂R, με x₁ < x₂. Τότε έχουμε:

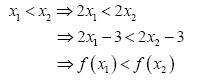
Γενικά:

Η συνάρτηση ƒ(x) = αx + β, με α < 0 είναι γνησίως φθίνουσα στο R.

Μια συνάρτηση που είναι είτε γνησίως αύξουσα είτε γνησίως φθίνουσα σε ένα διάστημα Δ λέγεται γνησίως μονότονη στο Δ.

Ελάχιστο και μέγιστο συνάρτησης

Ας θεωρήσουμε και πάλι τη γραφική παράσταση της συνάρτησης T = ƒ(t) .

Παρατηρούμε ότι:

α) Τη χρονική στιγμή t1 = 4 η θερμοκρασία του τόπου παίρνει την ελάχιστη τιμή της, που είναι η ƒ(4) = 3 βαθμοί Κελσίου. Δηλαδή ισχύει:

ƒ(t) ≥ ƒ(4) = 3 , για κάθε t[0,24]

Για το λόγο αυτό λέμε ότι η συνάρτηση T = ƒ(t) παρουσιάζει στο t = 4 ελάχιστο, το ƒ(4) = 3.

Γενικά:

ΟΡΙΣΜΟΣ

Μια συνάρτηση ƒ, με πεδίο ορισμού ένα σύνολο Α, λέμε ότι παρουσιάζει στο x₀Α (ολικό) ελάχιστο όταν:

ƒ(x) > ƒ(x₀), για κάθε xΑ

Το x₀Α λέγεται θέση ελαχίστου, ενώ το ƒ(x₀) ολικό ελάχιστο ή απλώς ελάχιστο της συνάρτησης ƒ και το συμβολίζουμε με min ƒ(x).

Για παράδειγμα, ας θεωρήσουμε τη συνάρτηση ƒ(x) = 3x4 + 1. Επειδή

x⁴ ≥ 0, για κάθε x,

θα είναι

3x⁴ ≥ 0, για κάθε xR ,

οπότε θα έχουμε

3x⁴ + 1 ≥ 1, για κάθε xR .

Επομένως:

ƒ(x) ≥ ƒ(0), για κάθε xR

Άρα, η ƒ παρουσιάζει ελάχιστο στο x₀ = 0 , το ƒ(0) = 1

β) Τη χρονική στιγμή t₂ = 16 η θερμοκρασία του τόπου παίρνει τη μέγιστη τιμή της, που είναι η T(16) = = 11 βαθμοί Κελσίου. Δηλαδή ισχύει:

ƒ(t) ≤ ƒ(16) = 11, για κάθε t[0,24]

Για το λόγο αυτό λέμε ότι η συνάρτηση T = ƒ(t) παρουσιάζει στο t = 16 μέγιστο, το ƒ(16) = 11. Γενικά:

ΟΡΙΣΜΟΣ

Μια συνάρτηση ƒ, με πεδίο ορισμού ένα σύνολο Α, λέμε ότι παρουσιάζει στο x₀Α (ολικό) μέγιστο όταν

ƒ(x) ≤ ƒ(x₀) , για κάθε xΑ

Το x₀Α λέγεται θέση μεγίστου, ενώ το ƒ(x₀) ολικό μέγιστο ή απλώς μέγιστο της ƒ και το συμβολίζουμε με max ƒ(x) .

Για παράδειγμα, ας θεωρήσουμε τη συνάρτηση ƒ(x) = –3x⁴ + 1. Επειδή

x⁴ ≥ 0, για κάθε xR,

θα είναι

–3x⁴ ≤ 0 , για κάθε xR,

οπότε θα έχουμε

–3x⁴ + 1 ≤ 1, για κάθε xR .

Επομένως:

ƒ(x) ≤ ƒ(0), για κάθε xR

Άρα, η ƒ παρουσιάζει μέγιστο στο x₀ = 0 , το ƒ(0) = 1.

Το (ολικό) μέγιστο και το (ολικό) ελάχιστο μιας συνάρτησης λέγονται ολικά ακρότατα αυτής.

ΣΧΟΛΙΟ

Μια συνάρτηση ενδέχεται να έχει και μέγιστο και ελάχιστο (Σχ. α) ή μόνο ελάχιστο (Σχ. β') ή μόνο μέγιστο (Σχ. γ') ή να μην έχει ούτε μέγιστο ούτε ελάχιστο (Σχ. δ').

Άρτια συνάρτηση

α) Στο παρακάτω σχήμα δίνεται η γραφική παράσταση Cƒ μιας συνάρτησης ƒ που έχει πεδίο ορισμού όλο το R . Παρατηρούμε ότι η Cf έχει άξονα συμμετρίας τον άξονα y'y, αφού το συμμετρικό κάθε σημείου της Cƒ ως προς τον άξονα y'y ανήκει στην Cƒ .

Επειδή, όμως, το συμμετρικό του τυχαίου σημείου M(x,y) της Cƒ ως προς τον άξονα y'y είναι το σημείο M'(–x,y) και επειδή τα σημεία M(x,y) και M'(–x,y) ανήκουν στην Cƒ , θα ισχύει y = ƒ(x) και y = ƒ(–x), οπότε θα έχουμε:

ƒ(–x) = ƒ(x)

Η συνάρτηση ƒ με την παραπάνω ιδιότητα λέμε λέγεται άρτια. Γενικά:

ΟΡΙΣΜΟΣ

Μια συνάρτηση ƒ, με πεδίο ορισμού ένα σύνολο Α, θα λέγεται άρτια, όταν για κάθε xΑ ισχύει:

–xΑ και ƒ(–x) = ƒ(x)

Η γραφική παράσταση μιας άρτιας συνάρτησης έχει άξονα συμμετρίας τον άξονα y 'y

Για παράδειγμα, η συνάρτηση ƒ(x) = 2x⁴ – x² + 1 είναι άρτια συνάρτηση, αφού έχει πεδίο ορισμού όλο το R και για κάθε xR ισχύει:

ƒ(–x) = 2(–x)⁴ – (–x)² + 1 = 2x⁴ – x² + 1 = ƒ(x)

Συνεπώς, η γραφική της παράσταση έχει άξονα συμμετρίας τον άξονα y'y .

Περιττή συνάρτηση

β) Στο παρακάτω σχήμα δίνεται η γραφική παράσταση Cƒ μιας συνάρτησης ƒ που έχει πεδίο ορισμού όλο το R .

Παρατηρούμε ότι η Cƒ έχει κέντρο συμμετρίας την αρχή των αξόνων, αφού το συμμετρικό κάθε σημείου της Cƒ ως προς την αρχή των αξόνων ανήκει στην Cƒ .

Επειδή, όμως, το συμμετρικό του τυχαίου σημείου M(x,y) της Cƒ ως προς την αρχή των αξόνων είναι το σημείο M'(–x, –y) και επειδή τα σημεία M(x,y) και M'(–x, –y) ανήκουν στην Cƒ , θα ισχύει y = ƒ(x) και –y = ƒ(–x), οπότε θα έχουμε:

ƒ(–x ) = –ƒ(x)

Η συνάρτηση f με την παραπάνω ιδιότητα λέγεται περιττή. Γενικά:

ΟΡΙΣΜΟΣ

Μια συνάρτηση ƒ, με πεδίο ορισμού ένα σύνολο Α, θα λέγεται περιττή, όταν για κάθε xΑ ισχύει:

–xΑ και ƒ(–x) = – ƒ(x)

Η γραφική παράσταση μιας περιττής συνάρτησης έχει κέντρο συμμετρίας την αρχή των αξόνων.

Για παράδειγμα, η συνάρτηση ƒ(x) = 2x³ – x είναι περιττή συνάρτηση, διότι έχει πεδίο ορισμού όλο το R και για κάθε xR ισχύει:

ƒ(–x) = 2(–x)³ – (–x) = –2x³ + x = – ƒ(x)

Συνεπώς, η γραφική της παράσταση έχει κέντρο συμμετρίας την αρχή των αξόνων.

ΣΗΜΕΙΩΣΗ

Ο όρος "άρτια" προέκυψε αρχικά από το γεγονός ότι οι συναρτήσεις y = x², y = x⁴, y = x⁶ κτλ., που έχουν άρτιο εκθέτη, έχουν άξονα συμμετρίας τον άξονα y'y, είναι δηλαδή άρτιες συναρτήσεις, ενώ ο όρος "περιττή" προέρχεται από το γεγονός ότι οι συναρτήσεις y = x , y = x³, y = x⁵ κτλ., που έχουν περιττό εκθέτη, έχουν κέντρο συμμετρίας την αρχή των αξόνων, είναι δηλαδή περιττές συναρτήσεις.

ΕΦΑΡΜΟΓΗ

Στο παρακάτω σχήμα δίνονται ορισμένα τμήματα της γραφικής παράστασης μιας άρτιας συνάρτησης ƒ που έχει πεδίο ορισμού το διάστημα [–6,6].

Να χαραχθούν και τα υπόλοιπα τμήματα της γραφικής παράστασης της συνάρτησης ƒ και με τη βοήθεια αυτής:

α) Να βρεθούν τα διαστήματα στα οποία η συνάρτηση ƒ:

i) είναι γνησίως αύξουσα,

ii) είναι γνησίως φθίνουσα

iii) είναι σταθερή.

β) Να βρεθεί η μέγιστη και η ελάχιστη τιμή της ƒ, καθώς επίσης οι θέσεις των ακροτάτων αυτών.

ΛΥΣΗ

Επειδή η συνάρτηση ƒ είναι άρτια, η γραφική της παράσταση θα έχει άξονα συμμετρίας τον άξονα y'y. Επομένως, αν πάρουμε τα συμμετρικά ως προς τον άξονα y'y των δοθέντων τμημάτων της γραφικής παράστασης της ƒ, θα έχουμε ολόκληρη τη γραφική παράσταση της ƒ, που είναι η πολυγωνική γραμμή Α΄Β΄ΓΌΓΒΑ (Σχήμα).

Από την παραπάνω γραφική παράσταση προκύπτει ότι:

α) Η συνάρτηση ƒ:

i) είναι γνησίως αύξουσα σε καθένα από τα διαστήματα [0,2] και [5,6],

ii) είναι γνησίως φθίνουσα σε καθένα από τα διαστήματα [–2,0] και [–6,–5], τα οποία είναι συμμετρικά ως προς το Ο των διαστημάτων [0,2] και [5,6] αντιστοίχως στα οποία η ƒ είναι γνησίως αύξουσα.

iii) είναι σταθερή σε καθένα από τα διαστήματα [–5,–2] και [2,5] τα οποία είναι συμμετρικά μεταξύ τους ως προς το Ο.

β) Η μέγιστη τιμή της ƒ είναι ίση με 4 και παρουσιάζεται όταν το x πάρει τις τιμές –6 και 6. Δηλαδή ισχύει:

max ƒ(x) = ƒ(–6) = ƒ(6) = 4

Η ελάχιστη τιμή της ƒ είναι ίση με 0 και παρουσιάζεται όταν το x πάρει την τιμή 0. Δηλαδή ισχύει:

min ƒ(x) = ƒ(0) = 0.

Ασκήσεις

Α' ΟΜΑΔΑΣ
1.	Να βρείτε τα διαστήματα στα οποία καθεμιά από τις παρακάτω συναρτήσεις είναι: α) γνησίως αύξουσα και β) γνησίως φθίνουσα.
2.	Να προσδιορίσετε τα ολικά ακρότατα των συναρτήσεων της προηγούμενης άσκησης, καθώς και τις θέσεις των ακροτάτων αυτών.
3.	Να δείξετε ότι: i) Η συνάρτηση ƒ(x) = x² – 6x +10 παρουσιάζει ελάχιστο για x = 3 . ii) Η συνάρτηση παρουσιάζει μέγιστο για x = 1.
4.	Να βρείτε ποιες από τις παρακάτω συναρτήσεις είναι άρτιες και ποιες είναι περιττές:
5.	Ομοίως για τις συναρτήσεις:
6.	Να βρείτε ποιες από τις παρακάτω γραμμές είναι γραφικές παραστάσεις άρτιας και ποιες περιττής συνάρτησης.
7.	Ομοίως για τις παρακάτω γραμμές
8.	Να συμπληρώσετε τις παρακάτω γραμμές ώστε να παριστάνουν γραφικές παραστάσεις α) Άρτιας συνάρτησης και β) Περιττής συνάρτησης.

ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ

Σε καθεμιά από τις παρακάτω περιπτώσεις να κυκλώσετε το γράμμα Α, αν ο ισχυρισμός είναι αληθής και το γράμμα Ψ, αν ο ισχυρισμός είναι ψευδής.

1.	Υπάρχει συνάρτηση της οποίας η γραφική παράσταση διέρχεται από τα σημεία Α (1,2) και Β(1,3).	Α	Ψ
2.	Οι ευθείες y = α² x – 2 και y = –x + 1 τέμνονται.	Α	Ψ
3.	Αν μία συνάρτηση f είναι γνησίως αύξουσα, τότε η – ƒ είναι γνησίως φθίνουσα.	Α	Ψ
4.	Μία γνησίως μονότονη συνάρτηση έχει το πολύ μία ρίζα.	Α	Ψ
5.	Υπάρχει γνησίως μονότονη συνάρτηση που διέρχεται από τα σημεία Α (1,2), Β(2,1) και Γ (3,3).	Α	Ψ
6.	Αν μια συνάρτηση ƒ είναι γνησίως φθίνουσα και έχει ρίζα τον αριθμό 1, τότε θα ισχύει ƒ(0) < 0 .	Α	Ψ
7.	Αν μια συνάρτηση ƒ είναι γνησίως μονότονη και η γραφική της παράσταση διέρχεται από τα σημεία Α (1,2) και Β (2,5), τότε η ƒ είναι γνησίως αύξουσα.	Α	Ψ
8.	Αν η μέγιστη τιμή μιας συνάρτησης ƒ είναι ίση με 1, τότε η εξίσωση ƒ(x) = 2 είναι αδύνατη.	Α	Ψ
9.	Η συνάρτηση με ƒ(x) = 3x² είναι άρτια.	Α	Ψ
10.	Αν μια συνάρτηση είναι άρτια ή περιττή και έχει ρίζα τον αριθμό ρ, τότε θα έχει ρίζα και τον αριθμό –ρ.	Α	Ψ
11.	Αν μία συνάρτηση ƒ είναι άρτια, τότε η ƒ δεν είναι γνησίως μονότονη.	Α	Ψ
12.	Αν μία συνάρτηση ƒ είναι άρτια, τότε η –ƒ είναι περιττή.	Α	Ψ

II.

Να επιλέξετε τη σωστή απάντηση για την παρακάτω συνάρτηση ƒ.

Η συνάρτηση ƒ, της οποίας η γραφική παράσταση προκύπτει από δύο διαδοχικές μετατοπίσεις της γραφικής παράστασης της συνάρτησης φ(x) = 3x⁴ μιας οριζόντιας κατά 1 μονάδα προς τα αριστερά και μιας κατακόρυφης κατά 2 μονάδες προς τα πάνω, έχει τύπο:

ΙΣΤΟΡΙΚΟ ΣΗΜΕΙΩΜΑ

Η ιδέα της χρησιμοποίησης διατεταγμένων ζευγών για τα σημεία ενός επιπέδου και της περιγραφής καμπύλων με εξισώσεις, ανήκει στον Rene Descartes (1596 – 1650) και στον Pierre de Fermat (1601 – 1665).

Ο Descartes (Καρτέσιος) γεννήθηκε στη La Haye (σημερινή Ντερκατ) της Touraine και πέθανε στη Στοκχόλμη. Σε ηλικία 10 χρόνων εγγράφηκε στο Βασιλικό Κολλέγιο της La Fleche, όπου δίδασκαν Ιησουίτες. Από εκείνη τη στιγμή αρχίζει και το ενδιαφέρον του για τα μαθηματικά. Στη ζωή του υπήρξε φιλόσοφος, αλλά ένα μεγάλο μέρος του χρόνου του το διέθετε για τα μαθηματικά.

Τα αποτελέσματα και οι μέθοδοί του, που δημοσίευσε το 1637 στο βιβλίο του Le Geometrie, δημιούργησαν ένα νέο κλάδο των μαθηματικών που αργότερα ονομάστηκε Αναλυτική Γεωμετρία.

Ο Καρτέσιος διείδε τη δύναμη της Άλγεβρας για τη λύση γεωμετρικών προβλημάτων και η σκέψη του αντιπροσώπευε μια ριζική απόκλιση από την μέχρι τότε επικρατούσα άποψη για τη Γεωμετρία. Ο όρος «Καρτεσιανές συντεταγμένες», οφείλεται στο όνομά του.

Ο Fermat, που έζησε στην Toulouse της νότιας Γαλλίας, αν και ήταν νομικός στο επάγγελμα, υπήρξε ένας από τους μεγαλύτερους μαθηματικούς του 17ου αιώνα.

Τις ιδέες του για συντεταγμένες στη Γεωμετρία, τυποποίησε στις αρχές του 1629 και τις κυκλοφόρησε με αλληλογραφία, αλλά δεν δημοσιεύτηκαν πριν από το 1679. Ο Fermat συνέδεσε το όνομά του με τον ισχυρισμό:

«Για κάθε ν > 2 είναι αδύνατο να βρούμε θετικούς ακέραιους α, β, γ που να ικανοποιούν την σχέση α^ν = β^ν + γ^ν ».

που είναι γνωστός ως το «τελευταίο θεώρημα του Fermat». Τον ισχυρισμό του αυτόν έγραψε ο Fermat στο περιθώριο ενός βιβλίου του προσθέτοντας και τα εξής:

«Έχω βρει μια πραγματικά θαυμάσια απόδειξη την οποία το περιθώριο αυτό είναι πολύ στενό για να χωρέσει».

Ο ισχυρισμός αυτός του Fermat αποδείχτηκε αληθής το 1994 από τον Άγγλο μαθηματικό Α. Wiles, αφού υπήρξε για 350 χρόνια ένα από τα διασημότερα άλυτα προβλήματα της Θεωρίας Αριθμών.