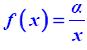7.2 ΜΕΛΕΤΗ ΤΗΣ ΣΥΝΑΡΤΗΣΗΣ: pic722

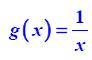
Η συνάρτηση pic723

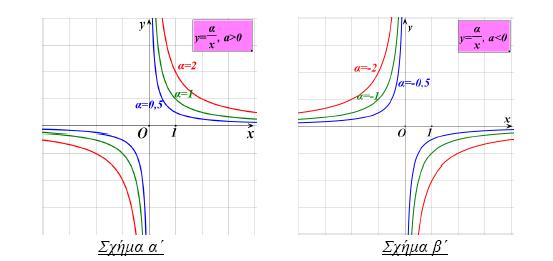
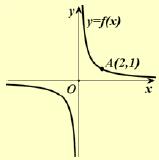
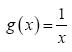Ας θεωρήσουμε τη συνάρτηση pic724. Παρατηρούμε ότι, η συνάρτηση αυτή έχει πεδίο ορισμού όλο το R+ = (–∞,0) U (0, +∞) και είναι περιττή, διότι για κάθε xpic03R ισχύει :

pic725

Επομένως, η γραφική της παράσταση έχει κέντρο συμμετρίας την αρχή των αξόνων. Γι’ αυτό αρχικά θα τη μελετήσουμε και θα την παραστήσουμε γραφικά στο διάστημα (0, +∞) .

Έχουμε λοιπόν:

  • Μονοτονία: Έστω τυχαία x1, x2 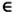pic03(0, +∞) με x11 < x2. Τότε θα ισχύει 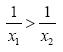pic726, οπότε θα έχουμε g(x1) > g(x2) . Άρα η συνάρτηση 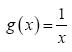pic724 είναι γνησίως φθίνουσα στο (0, +∞).
  • Πρόσημο των τιμών της g: Για κάθε x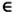pic03(0,+∞) ισχύει 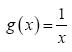pic724 >. Επομένως, στο διάστημα (0, +∞) η γραφική παράσταση της g θα βρίσκεται πάνω από τον άξονα των x.
  • Συμπεριφορά της g για "μικρές" τιμές του x: Ας θεωρήσουμε τον παρακάτω πίνακα τιμών της g για "πολύ μικρές" τιμές του x:

x

10–10 10–20 10–50 10–100 10–1000 ... pic72
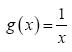pic724 1010 1020 1050 10100 101000 10... pic72

Παρατηρούμε ότι, καθώς το x μειώνεται απεριόριστα και παίρνει τιμές οσοδήποτε κοντά στο 0 ή, όπως λέμε, "τείνει στο 0", το pic727 αυξάνεται απεριόριστα και τείνει στο +∞. Αυτό σημαίνει ότι, καθώς το x "πλησιάζει" το 0 από τα δεξιά, η γραφική παράσταση της g τείνει να συμπέσει με τον ημιάξονα Oy . Γι’ αυτό ο άξονας y'y λέγεται κατακόρυφη ασύμπτωτη της γραφικής παράστασης της g προς τα πάνω.

  • Συμπεριφορά της g για "μεγάλες" τιμές του x: Ας θεωρήσουμε τον παρακάτω πίνακα τιμών της g για "πολύ μεγάλες" τιμές του x:

x

1010 1020 1050 10100 101000 ... pic72
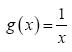pic724 10–10 10–20 10–50 10–100 10–1000 .... pic72

Παρατηρούμε ότι, καθώς το x αυξάνεται απεριόριστα και τείνει στο +∞, το μειώνεται απεριόριστα και τείνει στο 0. Αυτό σημαίνει ότι, καθώς το x "απομακρύνεται" προς το +∞, η γραφική παράσταση της g τείνει να συμπέσει με τον ημιάξονα Ox. Γι’ αυτό ο άξονας x'x λέγεται οριζόντια ασύμπτωτη της γραφικής παράστασης της g προς τα δεξιά.

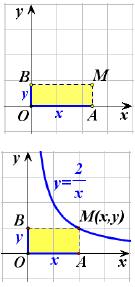
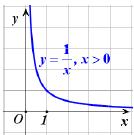Λαμβάνοντας υπόψη τα παραπάνω και παίρνοντας ένα πίνακα τιμών της g για θετικές τιμές του x , μπορούμε να χαράξουμε τη γραφική της παράσταση στο διάστημα (0, +∞) . pic729
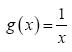Αν τώρα πάρουμε το συμμετρικό της παραπάνω καμπύλης ως προς την αρχή των αξόνων, τότε θα έχουμε τη γραφική παράσταση της pic724 σε όλο το R+, από την οποία συμπεραίνουμε ότι:

Η συνάρτηση pic724:

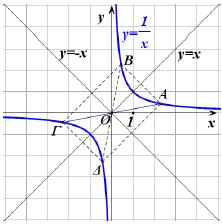 pic730
  • Είναι γνησίως φθίνουσα σε καθένα από τα διαστήματα (–∞,0) και (0, +∞) .
  • Έχει γραφική παράσταση η οποία:
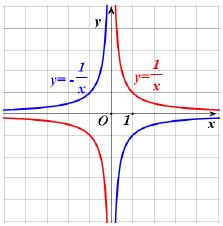
    • αποτελείται από δύο κλάδους, έναν στο 1ο και έναν στο 3ο τεταρτημόριο,
    • έχει κέντρο συμμετρίας την αρχή των αξόνων,
    • έχει άξονες συμμετρίας τις ευθείες y = x και y = –x, που διχοτομούν τις γωνίες των αξόνων και τέλος
    • έχει οριζόντια ασύμπτωτη τον άξονα x'x και κατακόρυφη ασύμπτωτη τον άξονα y' y .

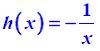
Η συνάρτηση pic731

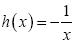Ας θεωρήσουμε τώρα τη συνάρτηση pic733. Παρατηρούμε ότι για κάθε xpic03R ισχύει

h(x) = – g(x) .

Επομένως, η γραφική παράσταση της pic733 είναι συμμετρική της γραφικής παράστασης της pic724 ως προς τον άξονα x'x, οπότε, η συνάρτηση pic733:

pic732
  • Είναι γνησίως αύξουσα σε καθένα από τα διαστήματα (–∞,0) και (0, +∞) .
  • Έχει γραφική παράσταση η οποία:
    • αποτελείται από δύο κλάδους, έναν στο 2ο και έναν στο 4ο τεταρτημόριο,
    • έχει κέντρο συμμετρίας την αρχή των αξόνων,
    • έχει άξονες συμμετρίας τις ευθείες y = x και y = –x, που διχοτομούν τις γωνίες των αξόνων και τέλος
    • έχει οριζόντια ασύμπτωτη τον άξονα x'x και κατακόρυφη ασύμπτωτη τον άξονα y' y.

Η συνάρτηση pic734

Διακρίνουμε δύο περιπτώσεις:

  • Αν α > 0, τότε εργαζόμαστε όπως εργαστήκαμε για τη συνάρτηση pic724 και καταλήγουμε στα ίδια συμπεράσματα.

Στο σχήμα α' δίνονται οι γραφικές παραστάσεις της pic735 για α = 0,5, α = 1 και α = 2 .

pic736

  • Αν α < 0, τότε εργαζόμαστε όπως εργαστήκαμε για τη συνάρτηση pic733 και καταλήγουμε στα ίδια συμπεράσματα.
    Στο σχήμα β' δίνονται οι γραφικές παραστάσεις της pic735 για α = –0,5 , α = –1 και α = –2.

Η γραφική παράσταση της συνάρτησης pic735 , με α ≠ 0, λέγεται ισοσκελής υπερβολή με κέντρο την αρχή των αξόνων και ασύμπτωτες τους άξονες x' x και y' y.

ΕΦΑΡΜΟΓΗ

Στο παρακάτω σχήμα το σημείο Μ κινείται στο 1ο τεταρτημόριο του συστήματος συντεταγμένων, έτσι ώστε το εμβαδόν του ορθογώνιου ΟΑΜΒ να παραμένει σταθερό και ίσο με 2τ.μ. Να αποδειχτεί ότι το σημείο Μ διαγράφει τον έναν κλάδο μιας ισοσκελούς υπερβολής.

ΛΥΣΗ

Αν με x συμβολίσουμε το μήκος και με y το πλάτος του ορθογωνίου, επειδή το εμβαδόν του είναι ίσο με 2τμ, θα ισχύει xy = 2 και x, y > 0 , οπότε θα έχουμε:

pic738

Άρα το σημείο Μ θα διαγράφει τον κλάδο της υπερβολήςpic739 που βρίσκεται στο 1ο τεταρτημόριο.

 pic737

Ασκήσεις

Α' ΟΜΑΔΑΣ
 

 

1.

Να βρείτε την εξίσωση της υπερβολής του διπλανού  σχήματος.

 pic740
2.

Στο ίδιο σύστημα συντεταγμένων να παραστήσετε γραφικά τις συναρτήσεις:

pic741
3.

Ομοίως τις συναρτήσεις:

pic742
4.

i) Στο ίδιο σύστημα συντεταγμένων να χαράξετε τις γραφικές παραστάσεις των συναρτήσεων pic743και g(x) = 1 και με τη βοήθεια αυτών να λύσετε γραφικά τις ανισώσεις:

pic744

ii) Να επιβεβαιώσετε και αλγεβρικά τα παραπάνω συμπεράσματα.
5.

Ομοίως για τις συναρτήσεις pic743 και g(x) = x2 και τις ανισώσεις:

pic744
6.

Οι κάθετες πλευρές ΑΒ και ΑΓ ενός ορθογώνιου τριγώνου pic745 μεταβάλλονται έτσι, ώστε το εμβαδόν του να παραμένει σταθερό και ίσο με 2 τετραγωνικές μονάδες. Να εκφράσετε το μήκος y της ΑΓ συναρτήσει του μήκους x της ΑΒ και στη συνέχεια να παραστήσετε γραφικά τη συνάρτηση αυτή.