7.3 ΜΕΛΕΤΗ ΤΗΣ ΣΥΝΑΡΤΗΣΗΣ ƒ(x) = αx² + βx + γ

Θα μελετήσουμε αρχικά τη συνάρτηση g(x ) = 2x² +12x + 20 που είναι ειδική περίπτωση της ƒ(x) = αx² + βx + γ με α ≠ 0.

Για τη μελέτη της συνάρτησης g μετασχηματίζουμε τον τύπο της ως εξής:

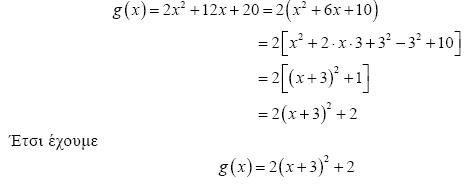
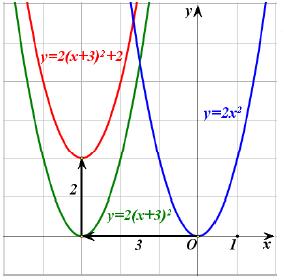
Επομένως, για να παραστήσουμε γραφικά την g , χαράσσουμε πρώτα την y = 2(x + 3)² που προκύπτει από μια οριζόντια μετατόπιση της y = 2x² κατά 3 μονάδες προς τα αριστερά, και στη συνέχεια χαράσσουμε την y = 2 (x + 3)² + 2 που προκύπτει από μια κατακόρυφη μετατόπιση της γραφικής παράστασης της y = 2(x + 3)² κατά 2 μονάδες προς τα πάνω.

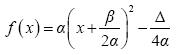
Επομένως η γραφική της παράστα-ση προκύπτει από δύο διαδοχικές μετατοπίσεις της παραβολής y = αx², μιας οριζόντιας και μιας κατακόρυ-φης, έτσι ώστε η κορυφή της να συμπέσει με το σημείο 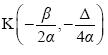. Συνεπώς είναι και αυτή μια παραβολή, που έχει κορυφή το σημείο 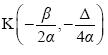άξονα συμμετρίας την ευθεία .

Άρα, η συνάρτηση ƒ(x) = αx² + βx + γ:

• Αν α > 0 ,

• Είναι γνησίως φθίνουσα στο διάστημα 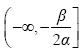και γνησίως αύξουσα στο διάστημα

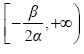
• Παρουσιάζει ελάχιστο για

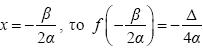
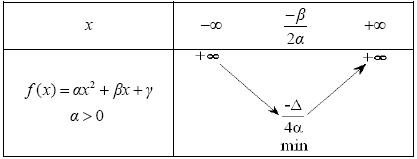
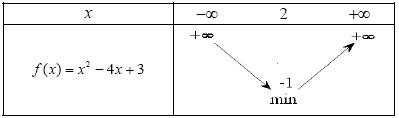
Τα συμπεράσματα αυτά συνοψίζονται στον παραπάνω πίνακα.

• Αν α < 0 , η συνάρτηση ƒ(x) = αx² + βx + γ:

• Είναι γνησίως αύξουσα στο διάστημα 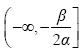και γνησίως φθίνουσα στο διάστημα

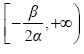
• Παρουσιάζει μέγιστο για

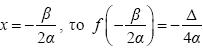
Τα συμπεράσματα αυτά συνοψίζονται στον πίνακα.

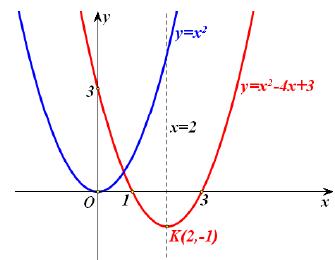
Τέλος η γραφική παράσταση της ƒ είναι μια παραβολή που τέμνει τον άξονα y'y στο σημείο Γ(0, y) , διότι ƒ(0) = γ, ενώ για τα σημεία τομής της με τον άξονα x'x παρατηρούμε ότι:

• Αν Δ > 0, το τριώνυμο αx2 + βx + γ έχει δύο ρίζες x₁ και x₂ και επομένως η παραβολή y = αx² + βx + γ τέμνει τον άξονα x'x σε δύο σημεία, τα Α(x₁,0) και Β(x₂,0) (Σχ. α')
• Αν Δ = 0, το τριώνυμο έχει διπλή ρίζα την 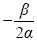. Στην περίπτωση αυτή λέμε ότι η παραβολή εφάπτεται του άξονα x'x στο σημείο 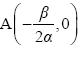(Σχ. β')
• Αν Δ < 0, το τριώνυμο δεν έχει πραγματικές ρίζες. Επομένως η παραβολή δεν έχει κοινά σημεία με τον άξονα x'x (Σχ. γ').

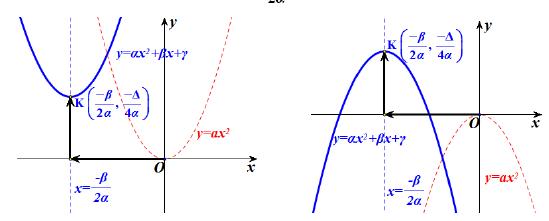
Η γραφική παράσταση της ƒ εξαρτάται από το πρόσημο των α και Δ και φαίνεται κατά περίπτωση στα παρακάτω σχήματα:

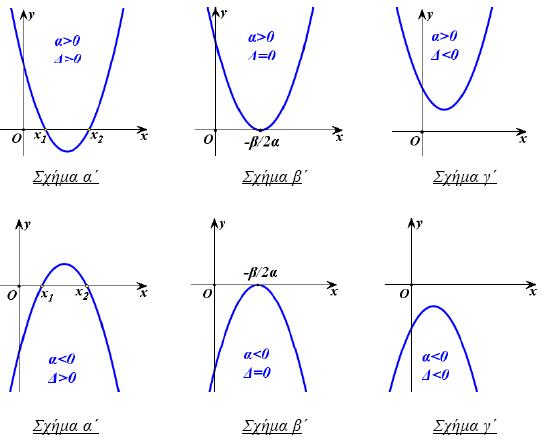
Τα συμπεράσματα της §3.2 για το πρόσημο του τριωνύμου προκύπτουν άμεσα και με τη βοήθεια των παραπάνω γραφικών παραστάσεων.

ΕΦΑΡΜΟΓΗ

Να μελετηθεί και να παρασταθεί γραφικά η συνάρτηση

ƒ(x) = x² – 4x + 3

ΛΥΣΗ

Για τη συνάρτηση ƒ(x) = x² – 4x + 3 είναι

Επομένως έχουμε τον πίνακα μεταβολών:

Δηλαδή η συνάρτηση ƒ,

• Είναι γνησίως φθίνουσα στο (–∞,2] και γνησίως αύξουσα στο [2, +∞),

• Παρουσιάζει για x = 2 ελάχιστο, το ƒ(2) = –1.

Επιπλέον, η γραφική παράσταση της ƒ είναι μια παραβολή η οποία:

• Έχει άξονα συμμετρίας την ευθεία x = 2 και

• Τέμνει τον άξονα  x'x  στα σημεία με τετμημένες 1 και 3 αντιστοίχως  που είναι οι ρίζες του τριωνύμου x² – 4x + 3 , και τον άξονα y'y στο σημείο με τεταγμένη 3.