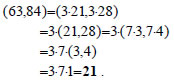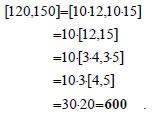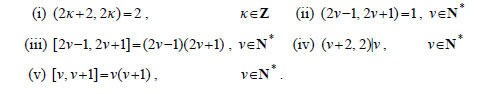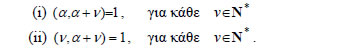4.4 ΜΕΓΙΣΤΟΣ ΚΟΙΝΟΣ ΔΙΑΙΡΕΤΗΣ - ΕΛΑΧΙΣΤΟ ΚΟΙΝΟ ΠΟΛΛΑΠΛΑΣΙΟ

Μέγιστος Κοινός Διαιρέτης

Έστω α,β δύο ακέραιοι. Ένας ακέραιος δ λέγεται κοινός διαιρέτης των α και β , όταν είναι διαιρέτης και του και του . Το σύνολο των θετικών κοινών διαιρετών δύο ακεραίων έχει ένα τουλάχιστον στοιχείο, αφού ο 1 είναι πάντα ένας θετικός κοινός διαιρέτης τους. Αν ένας τουλάχιστον από τους δύο ακεραίους είναι διαφορετικός από το 0, τότε το σύνολο των θετικών κοινών

διαιρετών τους είναι πεπερασμένο, και επομένως ανάμεσά τους υπάρχει μέγιστο στοιχείο. Αν όμως και οι δύο ακέραιοι είναι μηδέν, τότε κάθε θετικός ακέραιος είναι κοινός διαιρέτης τους και επομένως το σύνολο των θετικών κοινών διαιρετών τους δεν έχει μέγιστο στοιχείο.

ΟΡΙΣΜΟΣ

Έστω α και β δύο ακέραιοι, από τους οποίους ένας τουλάχιστον είναι διάφορος του μηδενός. Ορίζουμε ως μέγιστο κοινό διαιρέτη (Μ.Κ.Δ.) των α και β , και τον συμβολίζουμε με (α, β) , το μεγαλύτερο¹ από τους θετικούς κοινούς διαιρέτες τους.

Δηλαδή, ο Μ.Κ.Δ. δύο ακεραίων α και β είναι ο μοναδικός θετικός ακέραιος δ που έχει τις επόμενες δύο ιδιότητες: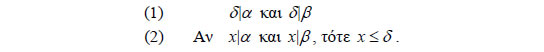

Από τον παραπάνω ορισμό προκύπτει ότι

Έτσι ,για παράδειγμα, αν α= -12 και β=30, τότε ( -12,30)=(12,30)=6 , αφού οι θετικοί διαιρέτες του 12 είναι οι 1,2,3,4,6,12 , του 30 οι 1,2,3,5,6,10,15,30 και ο μεγαλύτερος κοινός διαιρέτης τους είναι ο 6.

Παρατηρούμε επίσης ότι:

• Για κάθε θ ε τ ι κ ό ακέραιο α ισχύει (α,α)= α, (α,0)=α και (α,1)=1 .

• Αν α, β είναι δύο θ ε τ ι κ ο ί ακέραιοι με , τότε (α,β)= β .

Δύο ακέραιοι α και β , που έχουν μέγιστο κοινό διαιρέτη τη μονάδα, για τους οποίους δηλαδή ισχύει (α,β)= 1 , λέγονται πρώτοι μεταξύ τους. Για παράδειγμα, οι 28 και 15 είναι πρώτοι μεταξύ τους, αφού (28,15)=1 .

Αν για τον υπολογισμό του Μ.Κ.Δ. δύο ακεραίων προσδιορίζουμε προηγουμένως τους διαιρέτες τους, τότε, ιδιαίτερα για μεγάλους αριθμούς, απαιτείται πολύς χρόνος. Μια σύντομη και αποτελεσματική μέθοδος προσδιορισμού του Μ.Κ.Δ. οφείλεται στον Ευκλείδη και λέγεται ευκλείδειος αλγόριθμος. Ο αλγόριθμος αυτός στηρίζεται στο επόμενο θεώρημα.

ΘΕΩΡΗΜΑ 3

Αν α, β είναι δύο φυσικοί αριθμοί και υ είναι το υπόλοιπο της ευκλείδειας διαίρεσης του α με τον β , τότε

¹ Αποδεικνύεται ότι: "Κάθε πεπερασμένο υποσύνολο του R έχει μέγιστο στοιχείο".

ΑΠΟΔΕΙΞΗ

Έστω η ισότητα της ευκλείδειας διαίρεσης του 0 α με τον β . Αν και , τότε:

Ας χρησιμοποιήσουμε το παραπάνω θεώρημα στον υπολογισμό του Μ.Κ.Δ. των 111 και 78. Εφαρμόζοντας διαδοχικά την ευκλείδεια διαίρεση έχουμε: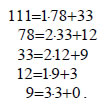

Επομένως,

δηλαδή (111,78)=3 , που είναι και το τελευταίο μη μηδενικό υπόλοιπο των διαδοχικών διαιρέσεων.

Γενικά, για δύο θετικούς ακεραίους α, β με 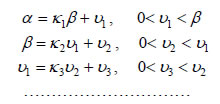, η διαδικασία μπορεί να περιγραφεί ως εξής: Εφαρμόζουμε επανειλημμένα και διαδοχικά την ευκλείδεια διαίρεση και γράφουμε

Από τον έλεγχο των ανισοτήτων στη δεξιά στήλη βλέπουμε ότι για την ακολουθία των διαδοχικών υπολοίπων ισχύει . Επομένως, ύστερα από β το πολύ βήματα θα εμφανιστεί το υπόλοιπο 0. Ας υποθέσουμε λοιπόν ότι

Τότε ισχύει (α,β)=υ_v . Αυτό προκύπτει από τη διαδοχική εφαρμογή του προηγούμενου θεωρήματος, σύμφωνα με το οποίο

Επομένως, ο Μ.Κ.Δ. των α και β είναι το τελευταίο θετικό υπόλοιπο των παραπάνω αλγοριθμικών διαίρεσεων.

Η διαδικασία αυτή αποτελεί τον ευκλείδειο αλγόριθμο και χρησιμοποιείται γενικότερα για τον προσδιορισμό του Μ.Κ.Δ. δύο οποιωνδήποτε ακεραίων.

Από τον παραπάνω αλγόριθμο μπορεί να προκύψει η πολύ σημαντική ιδιότητα του Μ.Κ.Δ. δύο αριθμών α, β, ότι δηλαδή αυτός μπορεί να εκφραστεί ως γραμμικός συνδυασμός των α και β.

Για παράδειγμα, από τη διαδικασία προσδιορισμού του Μ.Κ.Δ. των α=111 και β=78 έχουμε: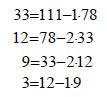

Επομένως,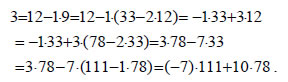

Ώστε

Γενικά, ισχύει:

ΘΕΩΡΗΜΑ 4

Αν δ είναι ο Μ.Κ.Δ. των α και β , τότε υπάρχουν ακέραιοι κ και λ, τέτοιοι, ώστε
                                                            

Δηλαδή, ο Μ.Κ.Δ. δύο ακέραιων μπορεί να γραφεί ως γραμμικός συνδυασμός των ακεραίων αυτών.

Οι ακέραιοι κ και λ δεν είναι μοναδικοί. Για παράδειγμα για το Μ.Κ.Δ. των 111 και 78 είναι αλλά και .

ΠΟΡΙΣΜΑ 1

Δύο ακέραιοι α, β είναι πρώτοι μεταξύ τους, αν και μόνο αν υπάρχουν ακέραιοι κ, λ , τέτοιοι, ώστε
                                                            

ΑΠΟΔΕΙΞΗ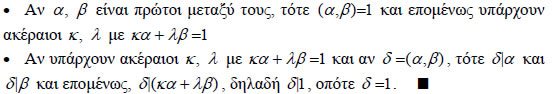

Αν κα + λβ= δ είναι η γραμμική έκφραση του μέγιστου κοινού διαιρέτη των ακεραίων α και β, τότε , που σημαίνει ότι .

Δηλαδή:

"Αν διαιρέσουμε δύο ακέραιους με το Μ.Κ.Δ. τους, προκύπτουν αριθμοί πρώτοι μεταξύ τους".

ΠΟΡΙΣΜΑ 2

Οι κοινοί διαιρέτες δύο ακεραίων α και β είναι οι διαιρέτες του μέγιστου κοινού διαιρέτη τους.

ΑΠΟΔΕΙΞΗ

Έστω δ=(α,β) . Προφανώς κάθε διαιρέτης του δ είναι και κοινός διαιρέτης των α και β . Αλλά και αντιστρόφως, κάθε κοινός διαιρέτης δ' των α και β είναι και διαιρέτης του Μ.Κ.Δ. των α,β. Πράγματι, αν κα + λβ=δ είναι η γραμμική έκφραση του δ , τότε ■

Για παράδειγμα, επειδή (150,120)=30 , οι θετικοί κοινοί διαιρέτες των 150 και 120 είναι οι διαιρέτες του 30, δηλαδή οι ακέραιοι 1,2,3,5,6,10,15 και 30.

ΠΟΡΙΣΜΑ 3

Αν για τους ακεραίους α,β,γ ισχύει και (α,β)=1 , τότε .

Δηλαδή, αν ένας ακέραιος διαιρεί το γινόμενο δύο ακεραίων και είναι πρώτος προς τον έναν, τότε διαιρεί τον άλλο.

ΑΠΟΔΕΙΞΗ

Επειδή (α,β)=1 , υπάρχουν ακέραιοι κ,λ , τέτοιοι, ώστε κα + λβ=1 και επομένως καγ + λβγ=γ . Αφού , θα ισχύει , δηλαδή . ■

Η συνθήκη (α,β)=1 είναι αναγκαία, για να ισχύει το θεώρημα. Για παράδειγμα, ενώ .

Η έννοια του μέγιστου κοινού διαιρέτη γενικεύεται και για περισσότερους από δύο ακεραίους. Συγκεκριμένα, αν α₁,α₂,α₃,...α_v, ακέραιοι με έναν τουλάχιστον διάφορο του μηδενός, τότε ορίζουμε ως μέγιστο κοινό διαιρέτη αυτών, και τον συμβολίζουμε με (α₁,α₂,α₃,...α_v), τον μεγαλύτερο από τους θετικούς κοινούς διαιρέτες τους. Αποδεικνύεται ότι:

"Ο Μ.Κ.Δ. τριών ή περισσότερων ακεραίων δε μεταβάλλεται αν αντικαταστήσουμε δύο από αυτούς με το μέγιστο κοινό διαιρέτη τους".

Για παράδειγμα (24,12,16)=((24,16),12)=(8,12)=4

Για το Μ.Κ.Δ. περισσότερων από δύο ακεραίους ισχύουν ανάλογες ιδιότητες με τις ιδιότητες του Μ.Κ.Δ. δύο ακεραίων. Έτσι ,για παράδειγμα, για τρεις ακέραιους α,β,γ αποδεικνύεται ότι: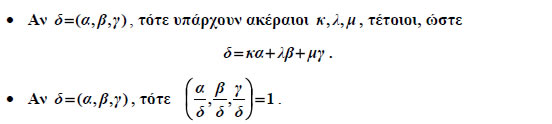

ΕΦΑΡΜΟΓΕΣ

1. Να αποδειχτεί ότι για τους ακεραίους α,β,κ ισχύουν

(i) (α,β)=(α -κβ,β)

(ii) (α,β)=(α -β,β)

(iii) (α,α +1)=1.

(i) Έστω δ=(α,β) και δ'=(α -κβ,β) , τότε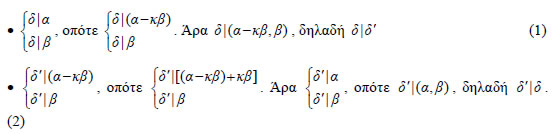

Από (1) και (2) έπεται ότι δ=δ'.
(ii) Λόγω της (i) , για κ=1 , ισχύει (α,β)=(α -β,β) .
(iii) Είναι: (α,α +1)=(α,α+1 -α)=1 .

2. Αν για τους ακεραίους α,β,γ ισχύει .

ΑΠΟΔΕΙΞΗ

Επειδή (α,β)=1 , υπάρχουν ακέραιοι κ,λ με κα + λβ=1 . Επομένως,

Όμως, , επομένως, γ=μα και γ=νβ . Έτσι, η (1) γίνεται κν(αβ)+λ(αβ)=γ . Άρα .

3. (i) Αν , να αποδειχτεί ότι (κα,κβ)=κ(α,β) .
(ii) Να βρεθεί ο Μ.Κ.Δ. των 63 και 84.

ΑΠΟΔΕΙΞΗ

(i) Έστω (α,β)=δ και (κα,κβ)=δ' . Αρκεί να δείξουμε ότι . Επειδή , έχουμε . Άρα .

Αφού δ=(α,β) , υπάρχουν ακέραιοι μ και ν με μα+νβ=δ και επομένως, κμα+κνβ=κδ . Όμως . Άρα .

(ii) Έχουμε

Ελάχιστο Κοινό Πολλαπλάσιο Ακεραίων

Ας θεωρήσουμε δύο ακεραίους α και β διαφορετικούς από το μηδέν. Ένας ακέραιος γ θα λέγεται κοινό πολλαπλάσιο των α και β , όταν είναι πολλαπλάσιο και του α και του β. Επειδή ο θετικός ακέραιος είναι κοινό πολλαπλάσιο των α και β, το σύνολο των θετικών πολλαπλάσιων των α και β είναι διάφορο του κενού συνόλου. Το ελάχιστο στοιχείο του συνόλου αυτού λέγεται ελάχιστο κοινό πολλαπλάσιο των α και β.

ΟΡΙΣΜΟΣ

Έστω δύο ακέραιοι α και β, διαφορετικοί από το μηδέν. Ορίζουμε ως ελάχιστο κοινό πολλαπλάσιο (Ε.Κ.Π.) των α και β, και το συμβολίζουμε με , το μικρότερο από τα θετικά κοινά πολλαπλάσια των α και β.

Επομένως, το Ε.Κ.Π. δύο μη μηδενικών ακεραίων α και β είναι ο μοναδικός θετικός ακέραιος ε που έχει τις επόμενες δύο ιδιότητες: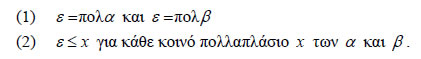

Από τον ορισμό προκύπτει ότι

Έτσι, για παράδειγμα, για τους ακεραίους -4 και 6 έχουμε [ -4,6]=[4,6]=12 , αφού τα θετικά πολλαπλάσια του 4 είναι 4,8,12,16,20,24,28,..., του 6 είναι τα 6,12,18,24,30,36,..., τα θετικά κοινά τους πολλαπλάσια είναι 12,24,36,... και το μικρότερο θετικό κοινό πολλαπλάσιο είναι το 12.

Παρατηρούμε επίσης ότι για θ ε τ ι κ ο ύ ς ακεραίους α, β ισχύει:

• Αν , τότε [α,β]= α .
• [α,1]=α.

ΘΕΩΡΗΜΑ 5

Αν α, β είναι δύο θ ε τ ι κ ο ί ακέραιοι, τότε

ΑΠΟΔΕΙΞΗ *

Αν (α,β)=δ , αρκεί να δείξουμε ότι , αρκεί δηλαδή να δείξουμε ότι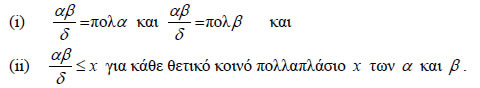

Επειδή (α,β)=δ , υπάρχουν θετικοί ακέραιοι μ και ν με α=μδ και β=vδ . Επομένως,

Αν x είναι ένα θετικό κοινό πολλαπλάσιο των α και β , τότε x=ρα και x=σβ , όπου ρ και σ θετικοί ακέραιοι. Ξέρουμε επίσης ότι υπάρχουν ακέραιοι κ,λ με δ=κα+λβ . Έτσι, αν θέσουμε 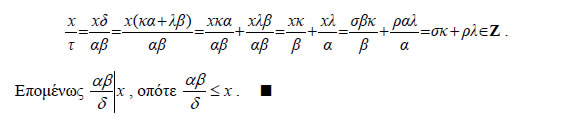, τότε θα έχουμε

Αν , τότε από τις ισότητες , έχουμε

Από το παραπάνω θεώρημα προκύπτουν δύο σημαντικά πορίσματα:

• Αν οι ακέραιοι α και β είναι πρώτοι μεταξύ τους, τότε .

Δηλαδή:

"Το Ε.Κ.Π. δύο πρώτων μεταξύ τους ακεραίων είναι το γινόμενο των απόλυτων τιμών τους".

Για παράδειγμα, .

• Το Ε.Κ.Π. δύο ακέραιων α,β διαιρεί κάθε άλλο κοινό πολλαπλάσιο x των α και β, δηλαδή είναι x=πολ[α,β]. Άρα:

"Τα κοινά πολλαπλάσια δύο ακεραίων είναι τα πολλαπλάσια του Ε.Κ.Π.".

Για παράδειγμα, τα κοινά πολλαπλάσια των 4 και 6 είναι πολλαπλάσια του [4,6]=12 , δηλαδή οι ακέραιοι

Η έννοια του ελάχιστου κοινού πολλαπλάσιου γενικεύεται και για περισσότερους από δύο ακεραίους. Συγκεκριμένα, αν , τότε ορίζουμε ως ελάχιστο κοινό πολλαπλάσιο (Ε.Κ.Π.) των ,α₁,α₂,α₃,...,α_v , και το συμβολίζουμε με [α₁,α₂,α₃,...,α_v] , το μικρότερο από τα θετικά κοινά τους πολλαπλάσια. Αποδεικνύεται ότι:

"Το ελάχιστο κοινό πολλαπλάσιο τριών ή περισσότερων ακεραίων δε μεταβάλλεται, αν αντικαταστήσουμε δύο από αυτούς με το ελάχιστο κοινό τους πολλαπλάσιο".

Για παράδειγμα, [4,6,16]= [[4,6],16]=[12,16]=48 .

ΕΦΑΡΜΟΓΗ

1. i) Να αποδειχτεί ότι [κα,κβ]=κ[α,β] για κάθε θετικό ακέραιο κ.

ii) Να βρεθεί το Ε.Κ.Π. των 120 και 150.

ΑΠΟΔΕΙΞΗ

(i) Έχουμε

(ii) Έχουμε

Ασκήσεις

Α' ΟΜΑΔΑΣ
1.	Να βρείτε το Μ.Κ.Δ. των ακεραίων α,β και να τον εκφράσετε ως γραμμικό συνδυασμό των α,β σε καθεμιά από τις παρακάτω περιπτώσεις
2.	Να αποδείξετε ότι:
3.	Να αποδείξετε ότι .