|
4.5 ΠΡΩΤΟΙ ΑΡΙΘΜΟΙ Εισαγωγή Δύο από τα σημαντικότερα αποτελέσματα σχετικά με τους πρώτους αριθμούς ήταν γνωστά ήδη από την αρχαιότητα. Το γεγονός ότι κάθε ακέραιος αναλύεται με μοναδικό τρόπο ως γινόμενο πρώτων εμφανίζεται στα "Στοιχεία" του Ευκλείδη στην εξής μορφή (βιβλίο IX, πρόταση 14): "Εάν ελάχιστος αριθμός υπό πρώτων αριθμών μετρήται, υπ' ουδενός άλλου πρώτου αριθμού μετρηθήσεται παρέξ των εξ αρχής μετρούντων". Στα "Στοιχεία" επίσης, το γεγονός ότι υπάρχουν άπειροι πρώτοι αριθμοί εμφανίζεται ως εξής (βιβλίο IX, πρόταση 20): "Οι πρώτοι αριθμοί πλείους εισί παντός του προτεθέντος πλήθους πρώτων αριθμών". Το αποτέλεσμα αυτό και η απόδειξή του από τον Ευκλείδη θεωρούνται ένα από τα αριστουργήματα της θεωρητικής μαθηματικής σκέψης. Ο G. Hardy (1877-1947) έγραψε ότι "… είναι τόσο σύγχρονο και σημαντικό όπως και όταν ανεκαλύφθη-εδώ και 2000 χρόνια παρέμεινε ανέπαφο". Ο μεγαλύτερος πρώτος αριθμός που έχει εντοπιστεί μέχρι σήμερα είναι ο 22.967.221-1 , ένας "γίγαντας" με 895.932 ψηφία. Πρόκειται για τον 36ο από τους πρώτους αριθμούς της μορφής 2v που γνωρίζουμε και ο οποίος οδήγησε στην ανακάλυψη του 36ου τέλειου αριθμού (βλπ. προηγούμενο ιστορικό σημείωμα). Οι τεράστιοι αυτοί αριθμοί εντοπίστηκαν με τη βοήθεια κριτηρίων αναγνώρισης πρώτων, που απαιτούν πολύωρη χρήση ηλεκτρονικών υπολογιστών. Άλλοι πρώτοι αριθμοί με ιδιαίτερο ενδιαφέρον είναι αυτοί της μορφής p=2v+1 , όπου v=2κ , από τους οποίους όμως γνωρίζουμε μόνο 5, αυτούς που προκύπτουν για κ=0,1,2,3,4 και είναι αντίστοιχα οι 3,5,17,257,65537 (όσοι από τους υπόλοιπους έχουν ελεγχθεί αποδείχτηκαν σύνθετοι). Ο C.F. Gauss σε πολύ νεαρή ηλικία έδειξε ότι ένα κανονικό πολύγωνο κατασκευάζεται με κανόνα και διαβήτη, μόνο αν το πλήθος των πλευρών του είναι πρώτος αριθμός αυτής της μορφής ή γινόμενο πρώτων αυτής της μορφής πολλαπλασιασμένο επί μια δύναμη του 2 ή απλώς μια δύναμη του 2. Το σημαντικότερο όμως ζήτημα σχετικά με τους πρώτους αριθμούς αφορά την κατανομή τους μέσα στην ακολουθία των φυσικών. Η κατανομή αυτή είναι πολύ ακανόνιστη, γιατί από τη μια μεριά υπάρχουν εκατομμύρια ζεύγη των λεγόμενων δίδυμων πρώτων, όπως ,για παράδειγμα, οι (29,31),(1451,1453),(299477,299479), ενώ από την άλλη υπάρχουν τεράστια κενά χωρίς κανέναν πρώτο. Μια σχετική τάξη στο χάος βάζει το "Θεώρημα των πρώτων αριθμών", σύμφωνα με το οποίο το πλήθος των πρώτων αριθμών που είναι μικρότεροι ή |
|
ίσοι από τον φυσικό ν δίνεται κατά προσέγγιση (καθώς το ν γίνεται πολύ μεγάλο) από τον τύπο . Αυτό το διαπίστωσαν εμπειρικά, μελετώντας πίνακες πρώτων αριθμών, οι A.M. Legendre και C.F. Gauss στα τέλη του 18ου αιώνα, ενώ η πρώτη αυστηρή απόδειξη δόθηκε 100 χρόνια αργότερα. Έννοια Πρώτου Αριθμού Παρατηρήσαμε προηγουμένως ότι κάθε ακέραιος ΟΡΙΣΜΟΣ Κάθε ακέραιος Για παράδειγμα, οι ακέραιοι 2 και -7 είναι πρώτοι, ενώ ο Ένας ακέραιος Οι αριθμοί 1 και -1 δε χαρακτηρίζονται ούτε ως πρώτοι ούτε ως σύνθετοι. Κάθε πρώτος που διαιρεί ένα δοθέντα ακέραιο λέγεται πρώτος διαιρέτης του ακεραίου αυτού. Είναι φανερό ότι ο -α είναι πρώτος, αν και μόνο αν ο α είναι πρώτος. Γι' αυτό στη συνέχεια θα περιοριστούμε μόνο σε θετικούς πρώτους. Ανάμεσα στους δέκα αριθμούς 1,2,3,...,10 οι 2,3,5 και 7 είναι πρώτοι, ενώ οι 4,6,8 και 10 είναι σύνθετοι. Ο αριθμός 2 είναι ο μοναδικός άρτιος που είναι πρώτος, όλοι οι άλλοι πρώτοι είναι περιττοί. Ένα εύλογο ερώτημα είναι το εξής: "Αν δοθεί ένας θετικός ακέραιος α , πώς μπορούμε να αποφανθούμε αν είναι πρώτος ή σύνθετος και, στην περίπτωση που είναι σύνθετος, πώς μπορούμε πρακτικά να βρούμε ένα διαιρέτη διαφορετικό από τους 1 και α "; Η προφανής απάντηση είναι να κάνουμε διαδοχικές διαιρέσεις με τους ακε-ραίους που είναι μικρότεροι του α . Αν κανένας από αυτούς δε διαιρεί τον α , τότε ο α είναι πρώτος. Αν και η μέθοδος αυτή είναι πολύ απλή στην περιγραφή της, δεν μπορεί να θεωρηθεί πρακτική, γιατί έχει απαγορευτικό κόστος σε χρόνο και εργασία, ιδιαίτερα για μεγάλους αριθμούς. Υπάρχουν ιδιότητες των σύνθετων ακεραίων που αναφέρονται στα επόμενα θεωρήματα και μας επιτρέπουν να περιορίσουμε σημαντικά τους αναγκαίους υπολογισμούς. |
|
ΘΕΩΡΗΜΑ 6 Κάθε θετικός ακέραιος μεγαλύτερος του 1 έχει έναν τουλάχιστον πρώτο διαιρέτη. ΑΠΟΔΕΙΞΗ Έστω ο θετικός ακέραιος ΠΟΡΙΣΜΑ 4 Αν α είναι ένας σύνθετος ακέραιος με ΑΠΟΔΕΙΞΗ Επειδή ο α είναι σύνθετος, γράφεται στη μορφή Υποθέτουμε ότι Το παραπάνω συμπέρασμα έχει μεγάλη πρακτική σημασία όταν εξετάζουμε αν
ένας ακέραιος Έστω, για παράδειγμα, ο ακέραιος α=271 . Επειδή Το Κόσκινο του Ερατοσθένη |
|
Μια έξυπνη τεχνική για τον προσδιορισμό των πρώτων που δεν υπερβαίνουν ένα θετικό ακέραιο στηρίζεται στο προηγούμενο θεώρημα και την οφείλουμε στον Αρχαίο Έλληνα μαθηματικό Ερατοσθένη (περίπου 250 π.Χ.). Η τεχνική λέγεται κόσκινο του Ερατοσθένη και είναι η εξής: Γράφουμε σε έναν πίνακα με αύξουσα σειρά τους ακεραίους από 2 μέχρι v .
Αφήνουμε τον πρώτο 2 και διαγράφουμε όλα τα πολλαπλάσιά του. Ο επόμενος
πρώτος στον πίνακα μετά τον 2 είναι ο 3. Αφήνουμε τον 3 και διαγράφουμε
όλα τα πολλαπλάσιά του κτλ. Συνεχίζουμε την ίδια διαδικασία μέχρι τον
πρώτο p με Στον παρακάτω πίνακα έχουν προσδιοριστεί οι πρώτοι μεταξύ 1 και 100.
Έχουν διαγραφεί τα πολλαπλάσια των πρώτων 2,3,5 και 7 , αφού ο επόμενος
πρώτος είναι ο αριθμός 11 και ισχύει 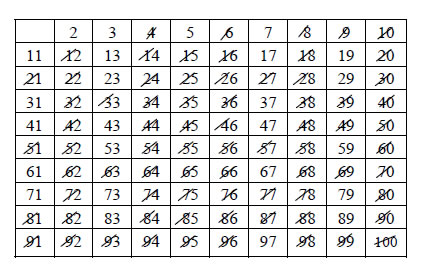 Στο σημείο αυτό πιθανόν να αναρωτηθεί κάποιος: Τελειώνουν κάπου οι πρώτοι; Υπάρχει δηλαδή μέγιστος πρώτος ή οι πρώτοι συνεχίζονται "επ'άπειρον"; ΘΕΩΡΗΜΑ 7 (του Ευκλείδη) Υπάρχουν ά π ε ι ρ ο ι θετικοί πρώτοι αριθμοί. |
|
ΑΠΟΔΕΙΞΗ Έστω ότι υπάρχει πεπερασμένο πλήθος πρώτων αριθμών
p1,p2,...,pv . Θα αποδείξουμε
ότι αυτό οδηγεί σε άτοπο. Σχηματίζουμε τον αριθμό Θεμελιώδες Θεώρημα Αριθμητικής Οι πρώτοι αριθμοί έχουν μεγάλη σπουδαιότητα για τη Θεωρία των Αριθμών, αφού, όπως θα αποδείξουμε στο Θεμελιώδες Θεώρημα της Αριθμητικής, κάθε φυσικός αναλύεται με μοναδικό τρόπο σε γινόμενο πρώτων παραγόντων. Με άλλα λόγια οι πρώτοι αριθμοί αποτελούν τα δομικά υλικά με τα οποία, μέσω του πολλαπλασιασμού κατασκευάζουμε τους άλλους φυσικούς αριθμούς, όπως για παράδειγμα στη Χημεία με κατάλληλα άτομα σχηματίζουμε τα μόρια των διάφορων ουσιών. Η απόδειξη του σημαντικού αυτού θεωρήματος στηρίζεται στον ακόλουθο αληθή ισχυρισμό. ΘΕΩΡΗΜΑ 8 Αν ένας πρώτος p διαιρεί το γινόμενο αβ δύο ακέραιων, τότε διαιρεί έναν, τουλάχιστον, από τους ακεραίους αυτούς. ΑΠΟΔΕΙΞΗ Έστω ότι Το θεώρημα ισχύει και για γινόμενο περισσότερων ακεραίων. Δηλαδή: "Αν p πρώτος και ΘΕΩΡΗΜΑ 9 Κάθε θετικός ακέραιος |
|
ΑΠΟΔΕΙΞΗ * • Αν ο α είναι πρώτος, τότε προφανώς το θεώρημα ισχύει. Αν ο α είναι σύνθετος, τότε, σύμφωνα με το θεώρημα 6, θα
ισχύει Αν ο β1 είναι πρώτος, τότε ο α είναι γινόμενο πρώτων παραγόντων και το θεώρημα αληθεύει. Αν ο β1 είναι σύνθετος, τότε θα έχουμε Αν ο β2 είναι πρώτος, τότε Αν ο β2 είναι σύνθετος, τότε η παραπάνω διαδικασία
μπορεί να συνεχιστεί και οδηγεί σε μια σχέση • Ας υποθέσουμε ότι ο α αναλύεται και με άλλο τρόπο σε γινόμενο πρώτων παραγόντων, ότι δηλαδή υπάρχουν και οι πρώτοι q1,q2,...,qλ , τέτοιοι, ώστε και έστω ότι Ο qμ όμως είναι πρώτος και έχει ως διαιρέτες μόνο
το 1 και τον εαυτό του. Άρα, επειδή |
|
Βέβαια, μερικοί από τους πρώτους παράγοντες που εμφανίζονται στην
ανάλυση ενός θετικού ακεραίου μπορεί να επαναλαμβάνονται όπως στην
περίπτωση του 360 για τον οποίο έχουμε Κάθε θετικός ακέραιος Η μορφή Μ.Κ.Δ. και Ε.Κ.Π. Αριθμών σε Κανονική Μορφή Όταν είναι γνωστή η ανάλυση ενός φυσικού αριθμού α σε πρώτους παράγοντες, εύκολα μπορούμε να επισημάνουμε τους διαιρέτες του. Έστω Με βάση την παρατήρηση αυτή μπορούμε εύκολα να βρούμε Μ.Κ.Δ. και το Ε.Κ.Π. αριθμών που έχουν αναλυθεί σε πρώτους παράγοντες. Συγκεκριμένα: • Ο Μ.Κ.Δ. θετικών ακεραίων που είναι γραμμένοι σε
κανονική μορφή είναι ίσος με το γινόμενο των κοινών τους παραγόντων και με
τον κάθε παράγοντα υψωμένο στο μικρότερο εμφανιζόμενο εκθέτη. |
|
Για παράδειγμα, επειδή ΕΦΑΡΜΟΓΕΣ 1. Να αποδειχτεί ότι αν ο
αριθμός ΑΠΟΔΕΙΞΗ Αν ο v δεν είναι πρώτος, τότεv=α,β με α,β
θετικούς ακέραιους και 2. Αν ο φυσικός αριθμός
v δεν είναι τετράγωνο φυσικού, να αποδειχτεί ότι ο αριθμός ΑΠΟΔΕΙΞΗ Έστω ότι ο αριθμός Ασκήσεις
| ||||
| ||||||||||||||||||||||||||
|