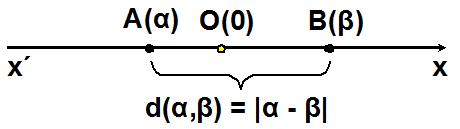2.3 ΑΠΟΛΥΤΗ ΤΙΜΗ ΠΡΑΓΜΑΤΙΚΟΥ ΑΡΙΘΜΟΥ

Ορισμός της απόλυτης τιμής

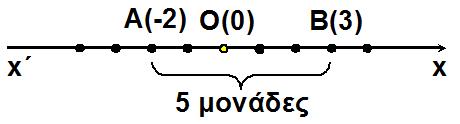
Θεωρούμε έναν αριθμό α που παριστάνεται με το σημείο Α πάνω σε έναν άξονα.

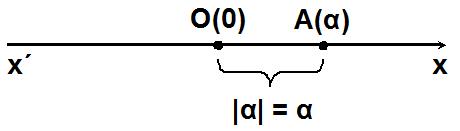
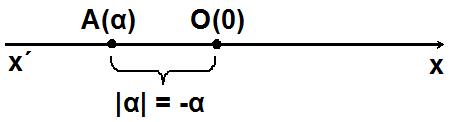
Γνωρίζουμε από το Γυμνάσιο ότι η απόσταση του σημείου Α από την αρχή Ο, δηλαδή το μήκος του ευθύγραμμου τμήματος ΟΑ, ονομάζεται απόλυτη τιμή του αριθμού α και την συμβολίζεται με |α|.
Από τον τρόπο με τον οποίο κατασκευάστηκε ο άξονας προκύπτει ότι:
— |2| = 2, , και γενικά: |α| = α , για κάθε α > 0.
Δηλαδή:
Η απόλυτη τιμή θετικού αριθμού είναι ο ίδιος ο αριθμός.

— |–2| = 2, , και γενικά |α| = –α , για κάθε α < 0.
Δηλαδή: Η απόλυτη τιμή αρνητικού αριθμού είναι ο αντίθετός του.

— |0| = 0
Επομένως, έχουμε τον ακόλουθο αλγεβρικό ορισμό της απόλυτης τιμής πραγματικού αριθμού.

Από τα προηγούμενα συμπεραίνουμε αμέσως ότι:

Για παράδειγμα,

• |x| = 5 x = 5 ή x = –5

• |α – β| = |2α – 3β|
  <=> α – β = 2α – 3β ή α – β = 3β – 2α
  <=> α = 2β ή

Ιδιότητες των απόλυτων τιμών

Από τον τρόπο εκτέλεσης των πράξεων μεταξύ πραγματικών αριθμών, προκύπτουν για τις απόλυτες τιμές οι ακόλουθες ιδιότητες:

1. |α · β| = |α| · |β| 2. 3. |α + β| ≤ |α| + |β|

Οι ιδιότητες αυτές, όμως, μπορούν να αποδειχθούν και με τη βοήθεια των προηγούμενων συμπερασμάτων.

ΑΠΟΔΕΙΞΗ

1. Επειδή και τα δύο μέλη της ισότητας |α · β| = |α| · |β| είναι μη αρνητικοί αριθμοί, έχουμε διαδοχικά:
|α · β| = |α| · |β|
|α · β|² = (|α| · |β|)²
|α · β|² = |α|² · |β|²
(α · β)² = α² · β² , που ισχύει.

2. Αποδεικνύεται με τον ίδιο τρόπο.

3. Επειδή και τα δύο μέλη της ανισότητας |α + β| < |α| + |β| είναι μη αρνητικοί αριθμοί, έχουμε διαδοχικά:
|α+β| ≤ |α| + |β|
<=>|α+β|² ≤ (|α| + |β|)²
<=> (α + β)² ≤ |α|² + |β|² + 2|α| · |β|
<=> α² + β² + 2αβ ≤ α² + β² + 2|αβ|
<=>αβ ≤ |αβ|, που ισχύει.

Είναι φανερό ότι η ισότητα αβ = |αβ| ισχύει αν και μόνο αν αβ ≥ 0 , δηλαδή αν και μόνο αν οι αριθμοί α και β είναι ομόσημοι ή ένας τουλάχιστον από αυτούς είναι ίσος με μηδέν.

ΣΧΟΛΙΟ

• Η ισότητα |α · β| = |α| · |β| ισχύει και για περισσότερους παράγοντες.

Συγκεκριμένα:
|α₁ · α₂ · ... · α_ν| = |α₁| · |α₂| · ... · |α_ν| Στην ειδική μάλιστα περίπτωση που είναι α₁ = α₂ = ... = α_ν = α, έχουμε:

|α^ν| = |α|^ν

• Η ανισότητα |α + β| ≤ |α| + |β| ισχύει και για περισσότερους προσθετέους.

Συγκεκριμένα:
|α₁ + α₂ + ... + α_ν| ≤ |α₁| + |α₂| + ... + |α_ν|

Απόσταση δυο αριθμών

• Ας πάρουμε τώρα δυο αριθμούς, για παράδειγμα τους –2 και 3, που παριστάνονται πάνω στον άξονα με τα σημεία Α και Β αντιστοίχως.

Το μήκος του τμήματος ΑΒ λέγεται απόσταση των αριθμών –2 και 3. Παρατηρούμε ότι (ΑΒ ) = 5 = |(–2) – 3| = |3 – (–2)|.
Γενικότερα, ας θεωρήσουμε δυο αριθμούς α και β που παριστάνονται πάνω στον άξονα με τα σημεία Α και Β αντιστοίχως.

Το μήκος του τμήματος ΑΒ λέγεται απόσταση των αριθμών α και β, συμβολίζεται με d(α,β) και είναι ίση με |α– β|. Είναι δηλαδή:

Προφανώς ισχύει d (α, β) = d (β, α) . Στην περίπτωση μάλιστα που είναι α < β, τότε η απόσταση των α και β είναι ίση με β – α και λέγεται μήκος του διαστήματος [α, β].

• Ας θεωρήσουμε τώρα ένα διάστημα [α, β] και ας ονομάσουμε Α και Β τα σημεία που παριστάνουν στον άξονα τα άκρα α και β αντιστοίχως.

Αν Μ (x0) είναι το μέσον του τμήματος AB, τότε έχουμε (MA) = (MB)
<=>d(x₀, α) = d(x₀, β)
<=>|x₀ – α| = |x₀ – β|
<=>x₀ – α = β – x₀, (αφού α < x₀ < β)
<=>2x₀ = α + β
<=>

Ο αριθμός που αντιστοιχεί στο μέσον Μ του τμήματος ΑΒ λέγεται κέντρο του διαστήματος [α, β], ενώ ο αριθμός λέγεται ακτίνα του [α, β].

Ως μήκος, κέντρο και ακτίνα των διαστημάτων (α, β), [α, β) και (α, β] ορίζουμε το μήκος, το κέντρο και την ακτίνα του διαστήματος [α, β].
— Έστω τώρα ότι θέλουμε να βρούμε τους πραγματικούς αριθμούς x για τους οποίους ισχύει |x – 3| < 2.

Από τον ορισμό της απόστασης έχουμε:
|x – 3| < 2 <=> d (x,3) < 2
<=> 3 – 2 < x < 3 + 2
<=> x (3 – 2, 3 + 2)

Γενικά:

Για x0 R και ρ > 0, ισχύει: |x – x0| < ρ <=> x (x0 – ρ, x0 + ρ) <=> x0 – ρ < x < x0 + ρ

Δηλαδή, οι αριθμοί x που ικανοποιούν τη σχέση |x –x₀| < ρ είναι τα σημεία του διαστήματος (x₀ – ρ, x₀ + ρ) που έχει κέντρο το x₀ και ακτίνα ρ.

Στην ειδική περίπτωση που είναι x0 = 0 , έχουμε:
|x| < ρ <=> x (–ρ, ρ) <=> –ρ < x < ρ . Για παράδειγμα, |x| < 2 <=> x (–2, 2) <=> –2 < x < 2 .

— Έστω, τώρα, ότι θέλουμε να βρούμε τους πραγματικούς αριθμούς x για τους οποίους ισχύει |x – 3| > 2.

Από τον ορισμό της απόστασης έχουμε:
|x – 3| > 2<=>d (x,3) > 2
     <=>x < 3 – 2 ή x > 3 + 2
     <=> x (–∞, 3 – 2) U (3 + 2, +∞).

Γενικά:

Για x0 R και ρ > 0, ισχύει: |x – x0| < ρ <=> x (–∞, x0 – ρ) U (x0 + ρ, +∞) <=> x < x0 – ρ ή x > x0 + ρ

Δηλαδή οι αριθμοί x που ικανοποιούν τη σχέση |x – x0| > ρ αντιστοιχούν σε σημεία Μ(x) του άξονα x΄x που απέχουν από το σημείο Κ(x₀) απόσταση μεγαλύτερη του ρ.

Στην ειδική περίπτωση που είναι x₀ = 0 , η τελευταία ισοδυναμία παίρνει τη μορφή:
   |x| > ρ <=> x < –ρ ή x > ρ
Για παράδειγμα:
   |x| > 2 <=> x < –2 ή x > 2 .

Ασκήσεις

Α' ΟΜΑΔΑΣ
1.	Να γράψετε τις παρακάτω παραστάσεις χωρίς απόλυτες τιμές. i) |π – 3|    ii) |π – 4|    iii) |3 – π| +|4 – π|    iv)
2.	Αν 3 < x < 4 , να γράψετε χωρίς την απόλυτη τιμή την παράσταση |x – 3| + |x – 4|
3.	Να γράψετε χωρίς την απόλυτη τιμή την παράσταση |x – 3| – |4 – x|, όταν: i) x < 3     ii) x > 4.
4.	Αν α ≠ β, να βρείτε την τιμή της παράστασης
5.	Αν x ≠ 0 και y ≠ 0, να βρείτε τις τιμές που μπορεί να πάρει η παράσταση
6.	Η διάμετρος ενός δίσκου μετρήθηκε και βρέθηκε 2,37dm. Το λάθος της μέτρησης είναι το πολύ 0,005dm. Αν D είναι η πραγματική διάμετρος του κύκλου, τότε: i) Να εκφράσετε την παραπάνω παραδοχή με τη βοήθεια της έννοιας της απόστασης ii) Να βρείτε μεταξύ ποιών ορίων βρίσκεται η τιμή D.
7.	Να συμπληρώσετε τον παρακάτω πίνακα όπως δείχνει η πρώτη γραμμή του.
Απόλυτη Τιμή Απόσταση Διάστημα ή ένωση διαστημάτων |x – 4| ≤ 2 d(x,4) ≤ 2 [2, 6] |x + 3| < 4 ........................ ........................ |x – 4| > 2 ........................ ........................ |x + 3| ≥ 4 ........................ ........................ ........................ d (x,5) < 1 ........................ ........................ d (x,–1) > 2 ........................ ........................ d (x,5) ≥ 1 ........................ ........................ d (x,–1) ≤ 2 ........................ ........................ ........................ (–2, 2) ........................ ........................ [–5, 1] ........................ ........................ (–∞, – 2] U [2, +∞)   ........................   (–∞, – 5) U (1, +∞)
B' ΟΜΑΔΑΣ
1.	Να αποδείξετε ότι       |α – β| ≤ |α – γ| + |γ – β|.
2.	Αν α > β, να αποδείξετε ότι:
3.	Τι σημαίνει για τους αριθμούς x και y : i) H ισότητα |x| + |y| = 0 ; ii) H ανισότητα |x| + |y| > 0;
4.	Έστω 0 < α < β . i) Να διατάξετε από τον μικρότερο στο μεγαλύτερο τους αριθμούς ii) Να δείξετε ότι στον πραγματικό άξονα ο αριθμός βρίσκεται πλησιέστερα στο 1 από ότι ο αριθμός .
5.	Αν |x – 2| < 0,1 και |y – 4| < 0,2 να εκτιμήσετε την τιμή της περιμέτρου των παρακάτω σχημάτων: