|
| 1 |
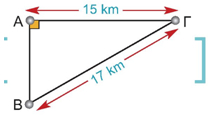
Η Πηνελόπη έγινε αρχιτέκτων! Πήρε επιτέλους το δίπλωμά της και γεμάτη όρεξη ρίχνεται στην πρώτη της δουλειά! Πρέπει να χτίσει ένα σπίτι με τετραγωνική βάση σε ένα γωνιακό οικόπεδο. Αφού ρώτησε την Πολεοδομία, πληροφορήθηκε ότι στο συγκεκριμένο οικόπεδο μπορεί κανείς να χτίσει σπίτι εμβαδού 289 m². Ποιο θα πρέπει να είναι το μήκος x κάθε πλευράς της τετραγωνικής βάσης του σπιτιού; |
Λύση
Γνωρίζουμε ότι το εμβαδόν του τετραγώνου είναι: Ε = x². Άρα πρέπει x² = 289
Δηλαδή, πρέπει να βρούμε έναν αριθμό x, του οποίου το τετράγωνο να είναι 289.
 |
Μήπως είναι x = 10; |
| Τότε όμως x² = 10² = 100 (θέλει πιο πολύ). |
 |
Μήπως είναι x = 20; |
| Τότε όμως x² = 20² = 400 (θέλει πιο λίγο). |
 |
Μήπως είναι x = 15; |
| Τότε όμως x² = 15² = 225 (θέλει λίγο πιο πολύ). |
 |
Μήπως είναι x = 17; |
| Τότε x² = 17² = 289 (αυτό είναι!). |
Το σπίτι θα έχει τετραγωνική βάση, πλευράς 17 (m).
Ο θετικός αριθμός 17, του οποίου το τετράγωνο ισούται με 289, ονομάζεται τετραγωνική ρίζα του 289 και
συμβολίζεται με 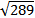 . Δηλαδή . Δηλαδή 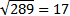
Γενικά:
Τετραγωνική ρίζα ενός θετικού αριθμού α, λέγεται ο θετικός αριθμός, ο οποίος, όταν υψωθεί στο τετράγωνο, δίνει τον αριθμό α. Η τετραγωνική ρίζα του α συμβολίζεται με 
|
Επειδή, 0² = 0, ορίζουμε ως |
 |

Σχόλια:
- Δεν ορίζουμε ρίζα αρνητικού αριθμού, γιατί δεν υπάρχει αριθμός που το τετράγωνό του να είναι αρνητικός. Για παράδειγμα η
 δεν έχει νόημα, γιατί κανένας αριθμός, όταν υψωθεί στο τετράγωνο, δε δίνει αποτέλεσμα -25. δεν έχει νόημα, γιατί κανένας αριθμός, όταν υψωθεί στο τετράγωνο, δε δίνει αποτέλεσμα -25.
- Από τον ορισμό της τετραγωνικής ρίζας, προκύπτει ότι:

- Σύμφωνα με τα παραπάνω:

|
|