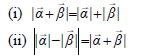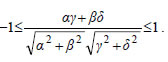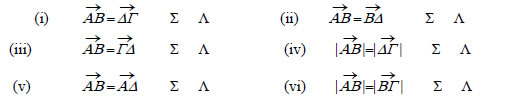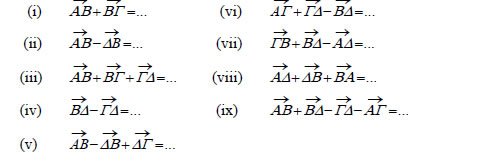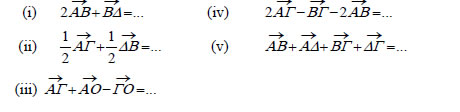|
1.5 ΕΣΩΤΕΡΙΚΟ ΓΙΝΟΜΕΝΟ ΔΙΑΝΥΣΜΑΤΩΝ 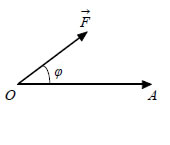 Γνωρίζουμε ότι το έργο που παράγεται από μια δύναμη ΟΡΙΣΜΟΣ • Ονομάζουμε εσωτερικό γινόμενο δύο μη
μηδενικών διανυσμάτων 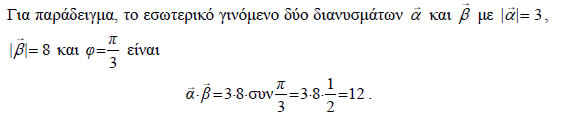
Άμεσες συνέπειες του παραπάνω ορισμού είναι οι εξής:  |
|
Ειδικότερα, για τα μοναδιαία διανύσματα Αναλυτική Έκφραση Εσωτερικού Γινομένου 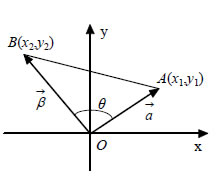 Θα δούμε τώρα πώς μπορούμε να εκφράσουμε το εσωτερικό γινόμενο δύο
διανυσμάτων η οποία ισχύει και στην περίπτωση που τα σημεία Ο,Α,Β είναι
συνευθειακά. Επομένως, έχουμε διαδοχικά: 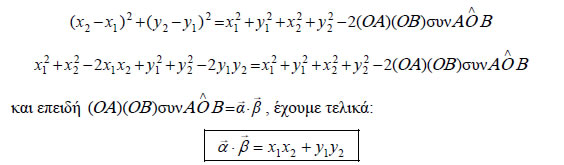
Δηλαδή: "Το εσωτερικό γινόμενο δύο διανυσμάτων είναι ίσο με το άθροισμα των γινομένων των ομώνυμων συντεταγμένων τους". Για παράδειγμα, το εσωτερικό γινόμενο των Με τη βοήθεια της αναλυτικής έκφρασης του εσωτερικού γινομένου θα αποδείξουμε ότι ισχύουν οι επόμενες ιδιότητες: |
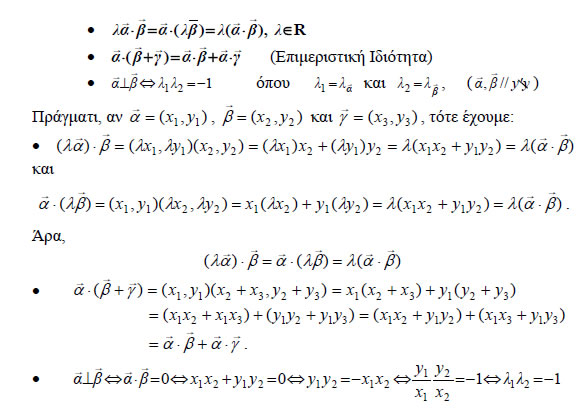 Συνημίτονο Γωνίας δύο Διανυσμάτων Αν 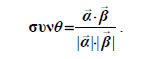 Είναι όμως Επομένως 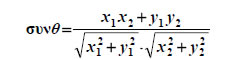 Για παράδειγμα, αν θ είναι η γωνία των διανυσμάτων 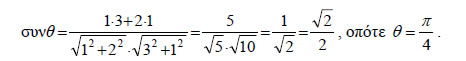 |
|
ΕΦΑΡΜΟΓΕΣ 1. Αν ΑΠΟΔΕΙΞΗ 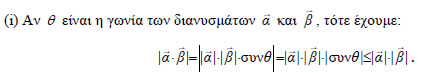 Η ισότητα ισχύει μόνο, αν Η ισότητα ισχύει, όπως και προηγουμένως, μόνο όταν 2. Έστω δύο διανύσματα ΛΥΣΗ Αν θ είναι η γωνία των Έχουμε λοιπόν 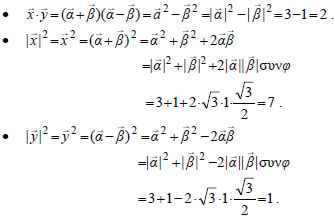
Άρα, |
|
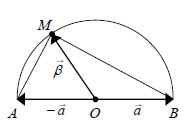
3. Να αποδειχτεί ότι ΑΠΟΔΕΙΞΗ 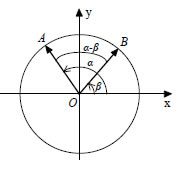 Αν στον τριγωνομετρικό κύκλο τα διανύσματα Επομένως, θα έχουμε: 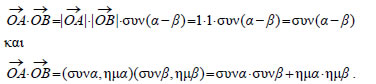
Άρα, Προβολή Διανύσματος σε Διάνυσμα Έστω 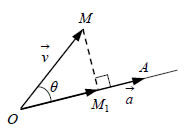 Το διάνυσμα Αποδεικνύεται ότι η προβολή του Για το εσωτερικό γινόμενο των Επομένως: |
|
ΕΦΑΡΜΟΓΕΣ 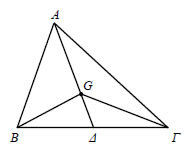 1. Να βρεθεί η προβολή του
διανύσματος ΛΥΣΗ Έστω 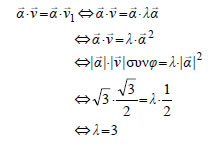 Άρα, 2.Δίνονται τα διανύματα ΛΥΣΗ 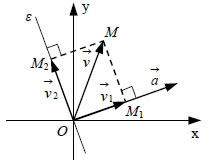 Έστω ε η ευθεία η κάθετη στη διεύθυνση του Το διάνυσμα 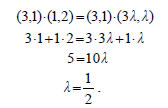 |
|
Συνεπώς, Ασκήσεις
| ||||||||||||||||||||
| ||||||||||||||||||||||||||||
|
ΓΕΝΙΚΕΣ ΑΣΚΗΣΕΙΣ
|
|
|
ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ
|
|
|
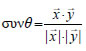 . Αρκεί, επομένως, να
υπολογίσουμε το
. Αρκεί, επομένως, να
υπολογίσουμε το