|
2Η ΕΥΘΕΙΑ ΣΤΟ ΕΠΙΠΕΔΟ Εισαγωγή Η ιδέα της χρησιμοποίησης ενός συστήματος συντεταγμένων για τον προσδιορισμό της θέσης ενός σημείου πάνω σε μια επιφάνεια προέρχεται από την Γεωγραφία και ήταν γνωστή στους αρχαίους γεωγράφους. Στην εφαρμογή αυτής της ιδέας στη Γεωμετρία στηρίζεται η έννοια της εξίσωσης μιας καμπύλης, δηλαδή της αλγεβρικής ισότητας που ικανοποιείται από τις συντεταγμένες των σημείων της καμπύλης (και μόνο αυτών). Η έννοια αυτή θεωρείται σήμερα τόσο απλή, ώστε η διδασκαλία της να αρχίζει από το Γυμνάσιο. Στην πραγματικότητα όμως η εξέλιξή της χρειάστηκε πολύ χρόνο και υπήρξε το αποτέλεσμα μιας σύνθεσης ανάμεσα στη Γεωμετρία και στην Άλγεβρα, με επαναστατικές συνέπειες για τα Μαθηματικά και τις Θετικές Επιστήμες. Η ανάγκη και τα πρώτα ίχνη ενός "συστήματος αναφοράς" εμφανίζονται στην αρχαία ελληνική Γεωμετρία κατά τη μελέτη των κωνικών τομών (δηλαδή της παραβολής, της υπερβολής και της έλλειψης, τις οποίες θα μελετήσουμε παρακάτω). Ο Απολλώνιος στο 1ο βιβλίο των "Κωνικών", αφού ορίζει αυτές τις καμπύλες στερεομετρικά ως τομές του κώνου από ένα επίπεδο, χρησιμοποιεί δύο συγκεκριμένες ευθείες του σχήματος, για να αποδείξει χαρακτηριστικές ιδιότητες κάθε καμπύλης. 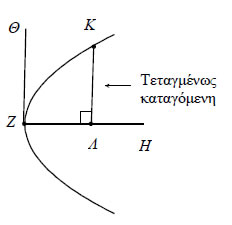 Για παράδειγμα, στην παραβολή του διπλανού σχήματος αποδεικνύει ότι αν φέρουμε την κάθετη ΚΛ ("τεταγμένως καταγόμενη") από σημείο της καμπύλης προς τη διάμετρο ΖΗ, τότε το τετράγωνο με πλευρά ΚΛ είναι ισοδύναμο με το ορθογώνιο που έχει πλευρές ΖΛ, ΖΘ, όπου ΖΘ ένα τμήμα κάθετο στην ΖΗ στην κορυφή καμπύλης (το μήκος του οποίου προσδιορίζεται από το είδος του κώνου και από τη θέση του τέμνοντος επιπέδου). |
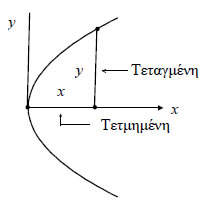 Η σχέση Η βασική διαφορά ανάμεσα στην αρχαία και στη σύγχρονη μέθοδο βρίσκεται στο γεγονός ότι η τελευταία χρησιμοποιεί τη συμβολική αναπαράσταση των γεωμετρικών σχέσεων και αξιοποιεί την ευελιξία του αλγεβρικού λογισμού (που εκφράζεται με τη χρήση αρνητικών συντεταγμένων κτλ.). Αυτό το αποφασιστικό βήμα έγινε γύρω στο 1630 από τους R. Descartes και P. Fermat, οι οποίοι επιχείρησαν να χρησιμοποιήσουν στη μελέτη δύσκολων προβλημάτων της αρχαίας ελληνικής Γεωμετρίας τη συμβολική Άλγεβρα που είχε δημιουργηθεί στη διάρκεια του 16ου αιώνα από τους Cardano, Viete κ.ά. Στα έργα των Descartes και Fermat δεν υπάρχουν οι άξονες συντεταγμένων ή οι εξισώσεις των καμπύλων που χρησιμοποιούμε σήμερα, αλλά περιγράφεται με συστηματικό τρόπο η διαδικασία αναγωγής ενός γεωμετρικού προβλήματος σε αλγεβρικό (ή αντίστροφα). Ιδιαίτερη επίδραση είχε το έργο του Descarte "La Gιomιtrie" (1637), στο οποίο –ακριβώς για να γίνει πιο αποτελεσματική η χρήση του αλγεβρικού λογισμού στη Γεωμετρία– εισάγονται νέοι συμβολισμοί (όπως, για παράδειγμα, η εκθετική γραφή των δυνάμεων), που φέρνουν ουσιαστικά την Άλγεβρα στη σημερινή μορφή της. Ύστερα από την πρώτη σύνθεση της Άλγεβρας και της Γεωμετρίας, οι εξελίξεις υπήρξαν ραγδαίες και οδήγησαν στην κεντρική έννοια της σύγχρονης Αναλυτικής Γεωμετρίας: "Η εξίσωση μιας καμπύλης, από βοηθητικό μέσο για τη λύση ενός γεωμετρικού προβλήματος, γίνεται μέσο ορισμού και αναπαράστασης αυτής της καμπύλης". Ο J. Wallis, στο βιβλίο του "Tractatus de sectionibus conicis" (1655), ορίζει την έλλειψη, την παραβολή και την υπερβολή τόσο με τον κλασικό τρόπο, ως τομές κώνου, όσο και με εξισώσεις 2ου βαθμού, ενώ ο I. Newton το 1676 χρησιμοποιεί με συστηματικό τρόπο δύο άξονες και αρνητικές συντεταγμένες, για να μελετήσει και να ταξινομήσει τις καμπύλες τρίτου βαθμού. Στην εργασία επίσης του Newton "Artis analyticae specimina vel geometria analytica" (που δημοσιεύτηκε το 1779) χρησιμοποιείται για πρώτη φορά ο όρος "Αναλυτική Γεωμετρία". Οι εξελίξεις αυτές, που έλαβαν χώρα παράλληλα με τη δημιουργία του διαφορικού και ολοκληρωτικού λογισμού, διαμόρφωσαν ένα νέο κλάδο των Μαθηματικών. Ο 2ος τόμος του κλασικού έργου του L. Euler "Introductio in analysin infinitorum" (1748) αποτελεί ένα πλήρες διδακτικό εγχειρίδιο |
|
Αναλυτικής Γεωμετρίας, στο οποίο οι καμπύλες του επιπέδου και οι επιφάνειες του χώρου ορίζονται και εξετάζονται αποκλειστικά μέσω των εξισώσεών τους ως προς ένα πλαγιογώνιο σύστημα συντεταγμένων. 2.1 ΕΞΙΣΩΣΗ ΕΥΘΕΙΑΣ Εξίσωση Γραμμής 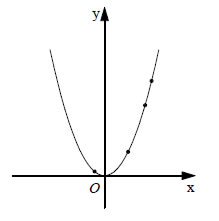 Αν έχουμε μια εξίσωση με δύο αγνώστους, για παράδειγμα την y=x2, τότε λύση της εξίσωσης αυτής λέγεται κάθε ζεύγος αριθμών (x,y) που την επαληθεύει. Έτσι, για παράδειγμα, τα ζεύγη (1,1), (2,4), (3,9), (0,0), (1/2,1/4), (√3,3) είναι λύσεις της y=x2. Αν τώρα σε ένα σύστημα συντεταγμένων παραστήσουμε με σημεία όλες τις λύσεις της εξίσωσης y=x2, τότε θα προκύψει η γραμμή C, του διπλανού σχήματος που, όπως γνωρίζουμε από προηγούμενες τάξεις λέγεται παραβολή. Επειδή οι συντεταγμένες (x,y) των σημείων M(x,y) της παραβολής C, και μόνο αυτές, επαληθεύουν την εξίσωση y=x2, γι'αυτό η εξίσωση y=x2 λέγεται εξίσωση της παραβολής C. Γενικά: Μια εξίσωση με δύο αγνώστους x,y λέγεται εξίσωση μιας γραμμής C, όταν οι συντεταγμένες των σημείων της C, και μόνο αυτές, την επαληθεύουν. Στη συνέχεια, αντί να λέμε, για παράδειγμα, "δίνεται η παραβολή C με
εξίσωση y=x2 ", θα λέμε "δίνεται η παραβολή Με τις εξισώσεις των γραμμών μπορούμε με αλγεβρικές μεθόδους να μελετήσουμε τις γεωμετρικές ιδιότητες των γραμμών αυτών ή να |
|
αντιμετωπίσουμε διάφορα άλλα συναφή προβλήματα. Αυτό είναι και το βασικό αντικείμενο της Αναλυτικής Γεωμετρίας. Συντελεστής Διεύθυνσης Ευθείας Η ευθεία γραμμή είναι η απλούστερη και η πιο συχνά χρησιμοποιούμενη γραμμή. Στην αναζήτηση της εξίσωσης μιας ευθείας θα μας διευκολύνει η έννοια του συντελεστή διεύθυνσης ευθείας. • Έστω Oxy ένα σύστημα συντεταγμένων στο επίπεδο και ε μια ευθεία που τέμνει τον άξονα x'x στο σημείο Α. 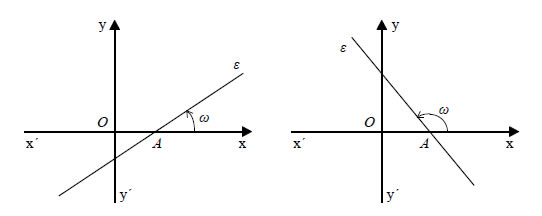 Τη γωνία ω που διαγράφει ο άξονας x'x όταν στραφεί
γύρω από το Α κατά τη θετική φορά μέχρι να συμπέσει με την ευθεία
ε τη λέμε γωνία που σχηματίζει η ε με τον άξονα
x'x. Αν η ευθεία ε είναι παράλληλη προς τον άξονα
x'x, τότε λέμε ότι σχηματίζει με αυτόν γωνία
ω=0. Σε κάθε περίπτωση για τη γωνία ω
ισχύει Στην περίπτωση που η γωνία της ευθείας ε με τον άξονα
x'x είναι 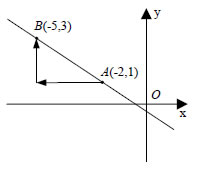 Όταν είναι γνωστά ένα σημείο μιας ευθείας και ο συντελεστής διεύθυνσης της ευθείας, τότε μπορούμε να σχεδιάσουμε την ευθεία. Για παράδειγμα, για να σχεδιάσουμε την ευθεία που διέρχεται από το σημείο Α(-2,1) και έχει |
|
συντελεστή διεύθυνσης • Έστω τώρα ένα διάνυσμα "Όταν μια ευθεία και ένα διάνυσμα είναι παράλληλα, έχουν τον ίδιο συντελεστή διεύθυνσης". 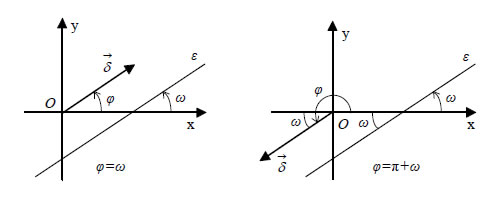 Αν είναι γνωστές οι συντεταγμένες δύο σημείων μιας μη κατακόρυφης
ευθείας ε, δηλαδή μιας ευθείας που δεν είναι κάθετη στον άξονα
x'x, τότε μπορούμε να βρούμε και το συντελεστή διεύθυνσης της
ευθείας αυτής. Πράγματι, αν Ο συντελεστής διεύθυνσης λ μιας ευθείας που
διέρχεται από τα σημεία |
|
Για παράδειγμα, ο συντελεστής διεύθυνσης της ευθείας που διέρχεται από
τα σημεία Α(1,-2) και Β(-1,4) είναι Συνθήκες Καθετότητας και Παραλληλίας Ευθειών Με τη βοήθεια του συντελεστή διεύθυνσης ευθείας, μπορούμε να
διατυπώσουμε τις συνθήκες παραλληλίας και καθετότητας δύο ευθειών στο
επίπεδο. Πράγματι, αν ε1,ε2 είναι δύο
ευθείες με αντίστοιχους συντελεστές διεύθυνσης
λ1,λ2 και τα διανύσματα 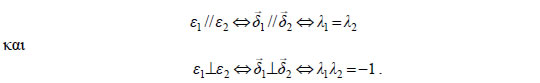 Επομένως, αν οι ευθείες ε1 και ε2 έχουν συντελεστές διεύθυνσης λ1 και λ2 αντιστοίχως, τότε: Εξίσωση Ευθείας Μια ευθεία στο επίπεδο καθορίζεται, όταν δίνονται ένα σημείο της και ο συντελεστής διεύθυνσής της ή δύο σημεία της. Θα βρούμε την εξίσωση της ευθείας σε καθεμιά από τις δύο αυτές περιπτώσεις 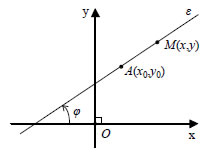 • Έστω Oxy ένα σύστημα συντεταγμένων στο επίπεδο και Α(x0,y0) ένα σημείο του επιπέδου. Ζητάμε την εξίσωση της ευθείας ε που διέρχεται από το Α και έχει συντελεστή διεύθυνσης λ. Ένα σημείο M(x,y) διαφορετικό του
Α(x0,y0) ανήκει στην ε, αν και
μόνο αν το διάνυσμα 1Με το συμβολισμό |
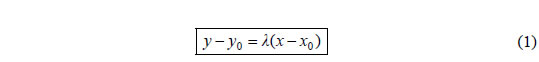 Για παράδειγμα, η ευθεία που διέρχεται από το σημείο Α(-1,2) και έχει συντελεστή διεύθυνσης λ=-3 έχει εξίσωση y-2=-3(x+1), δηλαδή y=-3x-1. 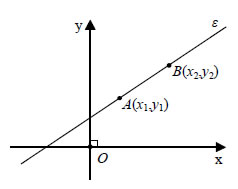 • Έστω ε η ευθεία που διέρχεται από τα σημεία 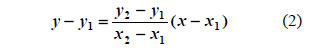 Οι εξισώσεις (1) και (2) δεν μπορούν να χρησιμοποιηθούν, όταν η ευθεία ε είναι κατακόρυφη, αφού στην περίπτωση αυτή δεν ορίζεται ο συντελεστής διεύθυνσης της ευθείας. Όμως η εξίσωση μιας κατακόρυφης ευθείας που διέρχεται από το σημείο Α(x0,y0) μπορεί να βρεθεί αμέσως, αφού κάθε σημείο της Μ έχει τετμημένη x0 και άρα η εξίσωσή της είναι: Για παράδειγμα, η ευθεία που διέρχεται από τα σημεία Α(-3,5)
και Β(4,1) έχει εξίσωση Ειδικές περιπτώσεις 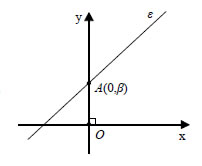 • Η εξίσωση ευθείας που τέμνει τον άξονα y'y στο σημείο
A(0,β) και έχει συντελεστή διεύθυνσης λ είναι |
 • Αν μια ευθεία διέρχεται από την αρχή των αξόνων και έχει συντελεστή διεύθυνσης λ, τότε η εξίσωσή της είναι y -0=λ(x-0) ή 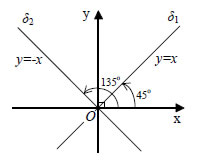 Έτσι, οι διχοτόμοι των γωνιών 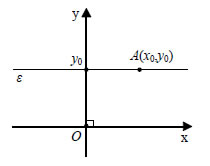 • Τέλος, αν μια ευθεία διέρχεται από το σημείο Α(x0,y0) και είναι παράλληλη στον άξονα x'x, δηλαδή είναι όπως λέμε μια οριζόντια ευθεία, έχει εξίσωση y-y0=0(x-x0) , δηλαδή ΕΦΑΡΜΟΓΕΣ 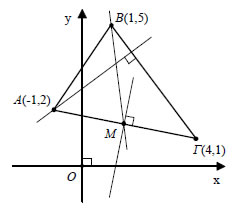 1. Δίνεται τρίγωνο με κορυφές τα σημεία A(-1,2), B(1,5) και Γ(4,1). Να βρεθούν οι εξισώσεις:
ΛΥΣΗ (i) Επειδή |
|
διεύθυνσης του ύψους του τριγώνου από το Α είναι (ii)Το μέσον Μ του τμήματος ΑΓ έχει συντεταγμένες
(iii)Επειδή η ευθεία ΑΓ έχει συντελεστή διεύθυνσης 2. Δίνονται η ευθεία
ε με εξίσωση ΛΥΣΗ 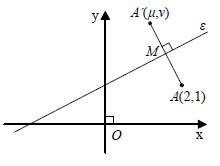 Αν A'(μ,ν) είναι το συμμετρικό του Α ως προς την
ε, τότε το μέσον Μ του AA' ανήκει στην
ε και το γινόμενο των συντελεστών διεύθυνσης των ε και
AA' είναι -1, αφού 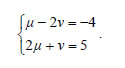 |
|
Από τη λύση του συστήματος αυτού βρίσκουμε Ασκήσεις
| ||||||||||||||||||
| ||||||||||||||
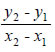 . Επομένως:
. Επομένως: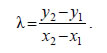
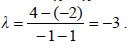
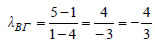 ο συντελεστής
ο συντελεστής 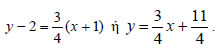 .
.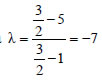 και άρα η
εξίσωση της ΒΜ είναι y -5= -7(x - 1), η οποία γράφεται
ισοδύναμα y= -7x + 12.
και άρα η
εξίσωση της ΒΜ είναι y -5= -7(x - 1), η οποία γράφεται
ισοδύναμα y= -7x + 12. 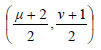 και ο
συντελεστής διεύθυνσης του AA' είναι
και ο
συντελεστής διεύθυνσης του AA' είναι 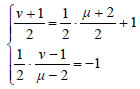 , το οποίο
μετά την εκτέλεση των πράξεων γράφεται
, το οποίο
μετά την εκτέλεση των πράξεων γράφεται