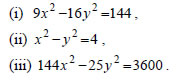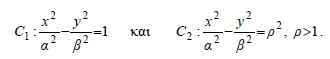|
3.4 Η ΥΠΕΡΒΟΛΗ Ορισμός Υπερβολής Έστω E' και Ε δύο σημεία ενός επιπέδου. Ονομάζεται υπερβολή με εστίες τα σημεία E' και Ε ο γεωμετρικός τόπος C των σημείων του επιπέδου των οποίων η απόλυτη τιμή της διαφοράς των αποστάσεων από τα E' και Ε είναι σταθερή και μικρότερη του (E'E). Την απόλυτη τιμή της διαφοράς των αποστάσεων κάθε σημείου της υπερβολής από τις εστίες την παριστάνουμε συνήθως με 2α, ενώ την απόσταση των εστιών με 2γ. Η απόσταση E'E ονομάζεται εστιακή απόσταση της υπερβολής. |
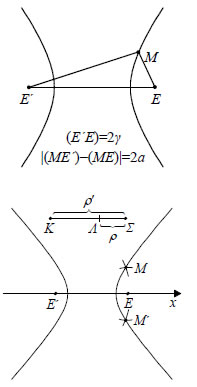 Σύμφωνα με τον ορισμό αυτό: α) Ένα σημείο Μ είναι σημείο της υπερβολής, αν και μόνο αν β) Ισχύει Για να βρούμε σημεία της υπερβολής C, εργαζόμαστε ως εξής: Παίρνουμε ένα ευθύγραμμο τμήμα ΚΛ μήκους 2α και ένα οποιοδήποτε σημείο Σ της ημιευθείας ΚΛ εκτός του ευθύγραμμου τμήματος ΚΛ. Με κέντρα E' και Ε και ακτίνες ρ' =(ΚΣ) και ρ =(ΛΣ) , αντιστοίχως, γράφουμε κύκλους οι οποίοι τέμνονται στα σημεία Μ και M' . Τα σημεία Μ και M' είναι σημεία της υπερβολής, γιατί ισχύει (ME') - (ME)=(KΣ) - (ΛΣ)=(ΚΛ)= 2α. Με τον τρόπο αυτό μπορούμε να κατασκευάσουμε οσαδήποτε σημεία της υπερβολής. Εξίσωση Υπερβολής • Έστω C μια υπερβολή με εστίες E' και Ε. Θα βρούμε την εξίσωση της C ως προς σύστημα συντεταγμένων Oxy με άξονα των x την ευθεία E'E και άξονα των y τη μεσοκάθετη του E'E. 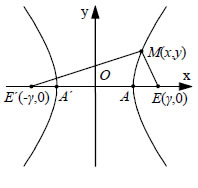 Αν M(x,y) είναι ένα σημείο της υπερβολής C, τότε θα ισχύει Επειδή (E'E)=2γ , οι εστίες E' και Ε θα έχουν συντεταγμένες ( -γ,0) και (γ,0) αντιστοίχως. Επομένως, Έτσι η σχέση (1) γράφεται |
|
από την οποία έχουμε διαδοχικά 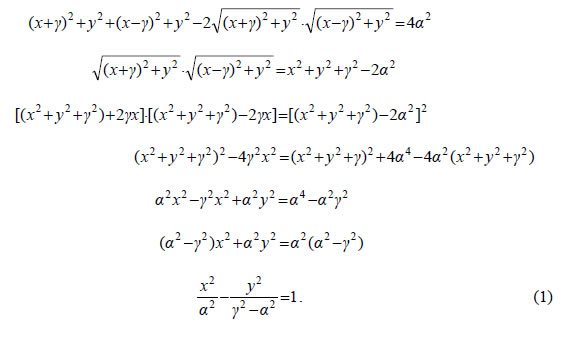 Επειδή 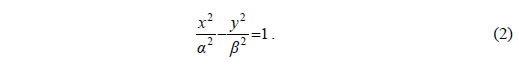 Αποδεικνύεται και το αντίστροφο, δηλαδή ότι κάθε σημείο M(x,y) του οποίου οι συντεταγμένες επαληθεύουν την εξίσωση (2) είναι σημείο της υπερβολής C. Επομένως, η εξίσωση της υπερβολής C με εστίες τα σημεία E'( -γ,0), E(γ,0) και σταθερή διαφορά 2α είναι  Για παράδειγμα, η εξίσωση της υπερβολής με εστίες τα σημεία E'( -13,0) E(13,0) και σταθερή διαφορά 2α=24 είναι 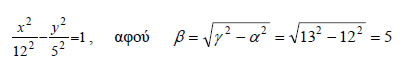 |
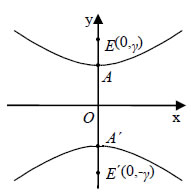 • Αν τώρα πάρουμε σύστημα συντεταγμένων Oxy με άξονα των y την ευθεία E'E και άξονα των x τη μεσοκάθετο του E'E και εργαστούμε όπως πριν, θα βρούμε ότι η εξίσωση της υπερβολής C είναι: 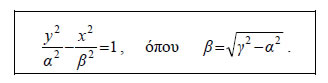 Για παράδειγμα, η εξίσωση της υπερβολής με εστίες τα σημεία E'(0, -13) E(0, 13) και σταθερή διαφορά 2α=24, είναι 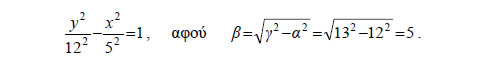 • Τέλος, αν είναι α=β, τότε η υπερβολή λέγεται ισοσκελής και η εξίσωσή της γράφεται: x2 - y2= α2. Ιδιότητες Υπερβολής Έστω μια υπερβολή C, η οποία ως προς ένα σύστημα συντεταγμένων
Oxy έχει εξίσωση 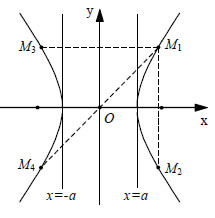 • Αν M1(x1,y1) είναι ένα σημείο της υπερβολής C, τότε και τα σημεία M2(x1, -y1) , M3( -x1, y1) και M4( -x1, -y1) ανήκουν στην C, αφού οι συντεταγμένες τους επαληθεύουν την εξίσωσή της. Αυτό σημαίνει ότι η υπερβολή C έχει τους άξονεςx'x και y'y άξονες συμμετρίας και την αρχή των αξόνων κέντρο συμμετρίας. Επομένως, η ευθεία που ενώνει τις εστίες E',E της υπερβολής και η μεσοκάθετη του E'E είναι άξονες συμμετρίας της υπερβολής, ενώ το μέσο Ο του E'E είναι κέντρο συμμετρίας της. Το σημείοΟ λέγεται κέντρο της υπερβολής. |
|
• Από την εξίσωση της υπερβολής για y=0 βρίσκουμε • Τέλος, από την εξίσωση της υπερβολής, έχουμε 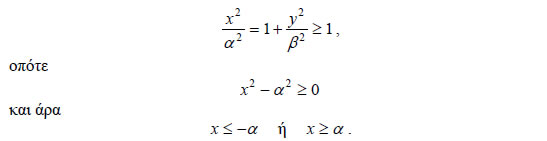
Επομένως, τα σημεία της υπερβολής C βρίσκονται έξω από την ταινία των ευθειών x= -α και x= α , πράγμα που σημαίνει ότι η υπερβολή αποτελείται από δύο χωριστούς κλάδους. Ασύμπτωτες Υπερβολής 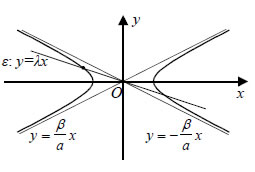 • Έστω μια υπερβολή C με εξίσωση 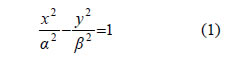
και μια ευθεία ε με εξίσωση δηλαδή μια ευθεία που περνάει από την αρχή των αξόνων. Η ευθεία ε έχει με την υπερβολή C κοινά σημεία, αν και μόνο αν το σύστημα 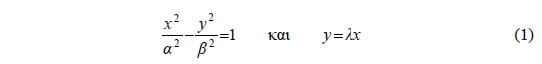
έχει λύση. Η πρώτη εξίσωση του συστήματος (1), λόγω της δεύτερης, γράφεται διαδοχικά 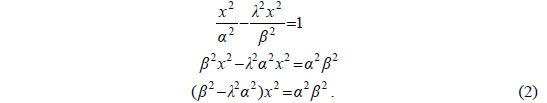 |
|
Έτσι το σύστημα (1) έχει λύση, αν και μόνο αν η (2) έχει λύση, δηλαδή
αν και μόνο αν 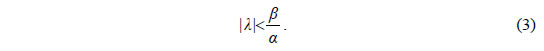
Επομένως, η ευθεία y=λx έχει με την υπερβολή κοινά σημεία, και
μάλιστα δύο, μόνο όταν 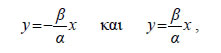 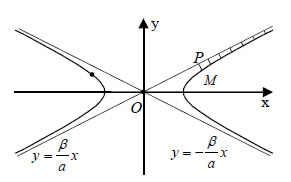 στις οποίες βρίσκεται ο άξονας x'x . Ας θεωρήσουμε τώρα ένα
σημείο M(x,y) της υπερβολής με 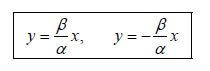 Είναι φανερό ότι οι ασύμπτωτες της υπερβολής είναι οι διαγώνιες του ορθογώνιου ΚΛΜΝ με κορυφές τα σημεία Κ(α,β), Λ(α, -β), Μ( -α, -β) και Ν( -α,β) . Το ορθογώνιο αυτό λέγεται ορθογώνιο βάσης της υπερβολής. Για |
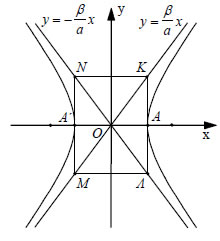 παράδειγμα, οι ασύμπτωτες της υπερβολής • Αν η υπερβολή C έχει εξίσωση 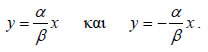 ΠΑΡΑΤΗΡΗΣΗ Ένας μνημονικός κανόνας για να βρίσκουμε κάθε φορά τις ασύμπτωτες μιας υπερβολής είναι ο εξής: Παραγοντοποιούμε το πρώτο μέλος της εξίσωσης της υπερβολής και
εξισώνουμε κάθε παράγοντα με μηδέν. Για παράδειγμα, έστω η υπερβολή 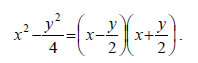 οι ασύμπτωτες της υπερβολής είναι οι ευθείες 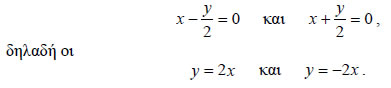 Εκκεντρότητα Υπερβολής Όπως στην έλλειψη έτσι και στην υπερβολή μία παράμετρος που καθορίζει
το σχήμα της είναι η εκκεντρότητα. Ονομάζουμε
εκκεντρότητα της υπερβολής 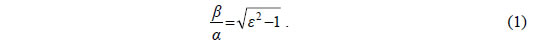
|
|
Επομένως, η εκκεντρότητα ε προσδιορίζει το συντελεστή διεύθυνσης της ασυμπτώτου της, δηλαδή χαρακτηρίζει το ορθογώνιο βάσης, άρα τη μορφή της ίδιας της υπερβολής. 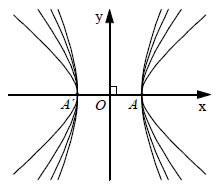 Όσο η εκκεντρότητα μικραίνει και τείνει να γίνει ίση με 1, ο λόγος β/α , άρα και το β, μικραίνει και τείνει να γίνει ίσο με 0. Κατά συνέπεια, όσο πιο μικρή είναι η εκκεντρότητα της υπερβολής τόσο πιο επίμηκες είναι το ορθογώνιο βάσης και κατά συνέπεια τόσο πιο κλειστή είναι η υπερβολή. Στην περίπτωση της ισοσκελούς υπερβολής είναι α=β , οπότε Εφαπτομένη Υπερβολής  • Έστω μια υπερβολή με εξίσωση 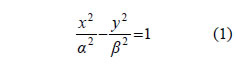
και ένα σημείο αυτής. H εφαπτομένη της υπερβολής στο σημείο M1(x1,y1) ορίζεται με τρόπο ανάλογο προς εκείνο με τον οποίο ορίστηκε η εφαπτομένη της έλλειψης και αποδεικνύεται ότι έχει εξίσωση 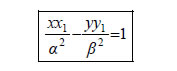 Έτσι, για παράδειγμα, η εφαπτομένη της υπερβολής • Αν μια υπερβολή έχει εξίσωση |
|
τότε η εφαπτομένη της στο σημείο M1(x1,y1) θα έχει εξίσωση 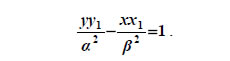 • Όπως η έλλειψη έτσι και η υπερβολή έχει ανάλογη ανακλαστική ιδιότητα. Συγκεκριμένα: Η εφαπτομένη μιας υπερβολής σε ένα σημείο της Μ
διχοτομεί τη γωνία 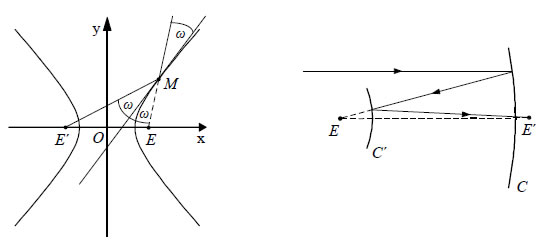 Επομένως, μια φωτεινή ακτίνα, κατευθυνόμενη προς τη μία εστία της υπερβολής, όταν ανακλάται στην επιφάνεια αυτής, διέρχεται από την άλλη εστία, όπως φαίνεται στο σχήμα. Η ιδιότητα αυτή της υπερβολής σε συνδυασμό με τις αντίστοιχες ιδιότητες των άλλων κωνικών τομών βρίσκει εφαρμογή στην κατασκευή των ανακλαστικών τηλεσκοπίων, καθώς και στη ναυσιπλοΐα για τον προσδιορισμό του στίγματος των πλοίων. ΕΦΑΡΜΟΓΗ 1.Να αποδειχτεί ότι το
γινόμενο των αποστάσεων ενός σημείου
M1(x1,y1) της υπερβολής |
|
ΑΠΟΔΕΙΞΗ Έστω M1(x1,y1) ένα σημείο της
υπερβολής. Τότε θα ισχύει Οι ασύμπτωτες ε1 και ε2 της
υπερβολής έχουν εξισώσεις αντιστοίχως. Επομένως, το γινόμενο των αποστάσεων του M1 από τις ε1, ε2 είναι ίσο με 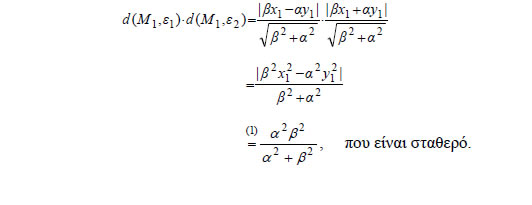 Ασκήσεις
| ||||
|
| ||||||||||||||
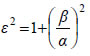 και άρα,
και άρα,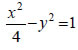 στο σημείο
στο σημείο 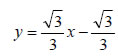 .
.