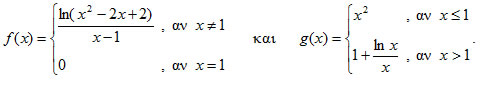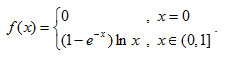|
2.9 ΑΣΥΜΠΤΩΤΕΣ - ΚΑΝΟΝΕΣ DE L' HOSPITAL Aσύμπτωτες
ΟΡΙΣΜΟΣ Αν ένα τουλάχιστον από τα όρια ● Για την ίδια συνάρτηση παρατηρούμε ότι :
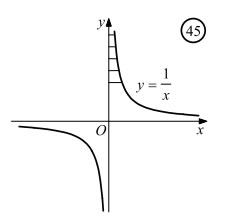
Αυτό σημαίνει ότι, καθώς το x τείνει στο +∞, η γραφική παράσταση της f τείνει να συμπέσει με την ευθεία y=0. Στην περίπτωση αυτή λέμε ότι η ευθεία y = 0 είναι οριζόντια ασύμπτωτη της Cf στο +∞. Επίσης παρατηρούμε ότι Αυτό σημαίνει ότι, καθώς το x τείνει στο −∞, η γραφική παράσταση της f τείνει να συμπέσει με την ευθεία y=0. Στην περίπτωση αυτή λέμε ότι η ευθεία y=0 είναι οριζόντια ασύμπτωτη της Cf στο −∞. Γενικά : |
|
ΟΡΙΣΜΟΣ Αν
ΟΡΙΣΜΟΣ
Η ασύμπτωτη y = λx + β είναι οριζόντια αν λ = 0, ενώ αν λ ≠0 λέγεται πλάγια ασύμπτωτη. Για τον προσδιορισμό των ασυμπτώτων μιας συνάρτησης ισχύει το παρακάτω θεώρημα, του οποίου η απόδειξη παραλείπεται. ΘΕΩΡΗΜΑ
| |||||||||||||
|
ΣΧΟΛΙΑ 1. Αποδεικνύεται ότι : — Οι πολυωνυμικές συναρτήσεις βαθμού μεγαλύτερου ή ίσου του 2 δεν έχουν ασύμπτωτες. — Οι ρητές συναρτήσεις 2. Σύμφωνα με τους παραπάνω ορισμούς, ασύμπτωτες της γραφικής παράστασης μιας συνάρτησης f αναζητούμε: — Στα άκρα των διαστημάτων του πεδίου ορισμού της στα οποία η f δεν ορίζεται. — Στα σημεία του πεδίου ορισμού της, στα οποία η f δεν είναι συνεχής. — Στο +∞, −∞, εφόσον η συνάρτηση είναι ορισμένη σε διάστημα της μορφής (α,+∞), αντιστοίχως (−∞,α).
ΕΦΑΡΜΟΓH Nα βρεθούν οι ασύμπτωτες της γραφικής παράστασης της συνάρτησης ΛΥΣΗ Επειδή η f έχει πεδίο ορισμού το R* και ειναι συνεχής σ' αυτό, θα αναζητήσουμε κατακόρυφη ασύμπτωτη στο 0 και πλάγιες στο −∞ και +∞ . Είναι Άρα, η ευθεία x = 0 είναι κατακόρυφη ασύμπτωτη της γραφικής παράστασης της f. Eξετάζουμε, τώρα, αν υπάρχει στο +∞ ασύμπτωτη της μορφής y = λx + β. Έχουμε :
Επομένως, η ευθεία y = x είναι πλάγια ασύμπτωτη της γραφικής παράστασης της f στο +∞. Ανάλογα βρίσκουμε ότι η ευθεία y = x είναι πλάγια ασύμπτωτη της γραφικής παράστασης της f και στο −∞. |
|
Κανόνες de L' Hospital Έστω η συνάρτηση
Παρατηρούμε ότι, αν εφαρμόσουμε τον κανόνα του ορίου
πηλίκου, παρουσιάζεται απροσδιοριστία της μορφής ΘΕΩΡΗΜΑ 1ο (μορφή
Έτσι το παραπάνω όριο (1) υπολογίζεται ως εξής : Έχουμε: και Επομένως : που σημαίνει ότι η ευθεία x = 0 είναι κατακόρυφη ασύμπτωτη της γραφικής παράστασης της f. |
|
ΘΕΩΡΗΜΑ 2ο (μορφή
Για παράδειγμα, ο υπολογισμός του Έχουμε : και
Επομένως : ΣΧΟΛΙΑ 1. Το θεώρημα 2 ισχύει και για τις μορφές 2. Τα παραπάνω θεωρήματα ισχύουν και για πλευρικά όρια και μπορούμε, αν χρειάζεται, να τα εφαρμόσουμε περισσότερες φορές, αρκεί να πληρούνται οι προϋποθέσεις τους.
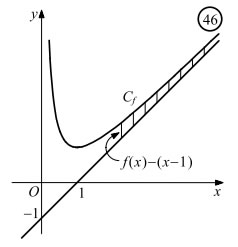
ΕΦΑΡΜΟΓEΣ 1. Δίνεται η συνάρτηση i) Η ευθεία y = x + 2 είναι ασύμπτωτη της Cf στο −∞ ii) Η ευθεία y = x − 2 είναι ασύμπτωτη της Cf στο +∞.
ΑΠΟΔΕΙΞΗ |
|
i) Αρκεί να δείξουμε ότι Πράγματι, έχουμε ii) Αρκεί να δείξουμε ότι Πράγματι, έχουμε
2. Να βρεθούν οι ασύμπτωτες της γραφικής παράστασης της συνάρτησης ΛΥΣΗ Επειδή η συνάρτηση f είναι συνεχής στο R η γραφική της παράσταση δεν έχει κατακόρυφες ασύμπτωτες. Θα αναζητήσουμε, επομένως, ασύμπτωτες στο −∞ και στο +∞.
Άρα, η ευθεία y = 0, δηλαδή ο άξονας xʹx, είναι ασύμπτωτη της Cf στο +∞. |
|
ΑΣΚΗΣΕΙΣ
1. Nα βρείτε (αν υπάρχουν) τις κατακόρυφες ασύμπτωτες των γραφικών παραστάσεων των συναρτήσεων:
2. Nα βρείτε τις οριζόντιες ασύμπτωτες των γραφικών παραστάσεων των συναρτήσεων :
3. Nα βρείτε τις ασύμπτωτες των γραφικών παραστάσεων των συναρτήσεων:
4. Nα υπολογίσετε τα παρακάτω όρια :
1. Δίνεται η συνάρτηση i) H ε1 είναι ασύμπτωτη της Cf στο −∞, ενώ η ε2 είναι ασύμπτωτη της Cf στο +∞. ii) Για κάθε x ϵ R ισχύει x2 + 2x + 2 > (x + 1)2 ≥ 0 και στη συνέχεια να αποδείξετε ότι η Cf βρίσκεται πάνω από την ε1 κοντά στο −∞ και πάνω από την ε2 κοντά στο +∞ . |
|
2. Να βρείτε τις ασύμπτωτες της γραφικής παράστασης της f όταν :
3. Nα βρείτε τις τιμές των α,β ϵ R, ώστε η συνάρτηση
να είναι παραγωγίσιμη στο x0 = 0. 4. Δίνεται η συνάρτηση
5. Δίνονται οι συναρτήσεις
Να αποδείξετε ότι : i) Η f είναι συνεχής και παραγωγίσιμη στο x0 = 1, ενώ ii) Η g είναι συνεχής αλλά μη παραγωγίσιμη στο x0 = 1.
6. Δίνεται η συνάρτηση
i) Να υπολογίσετε τα όρια ii) Nα αποδείξετε ότι η f είναι συνεχής στο 0. iii) Να βρείτε την εξίσωση της εφαπτομένης της Cf στο σημείο Ο(0,0). |
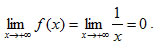
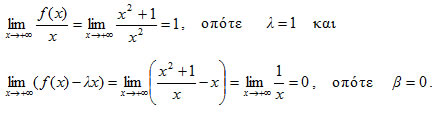
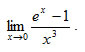
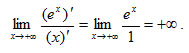
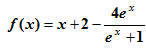 . Να αποδειχτεί ότι :
. Να αποδειχτεί ότι :
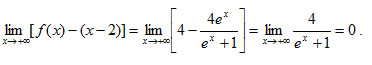

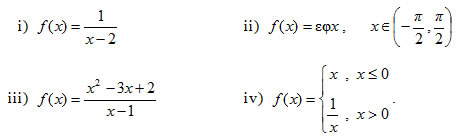

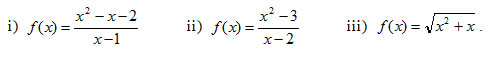
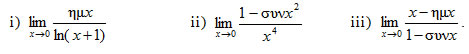
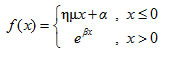
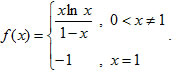 Να
αποδείξετε ότι :
Να
αποδείξετε ότι :