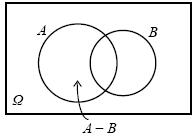
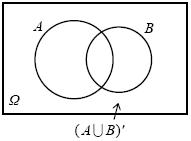
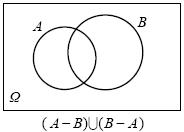
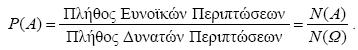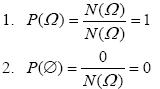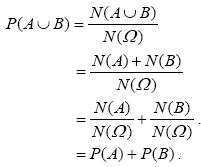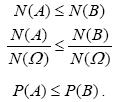Εισαγωγή
Ένα από τα κύρια χαρακτηριστικά του πειράματος τύχης, όπως είδαμε, είναι η αβεβαιότητα για το ποιο αποτέλεσμα του πειράματος θα εμφανιστεί σε μια συγκεκριμένη εκτέλεσή του. Επομένως, αν Α είναι ένα ενδεχόμενο, δεν μπορούμε με βεβαιότητα να προβλέψουμε αν το Α θα πραγματοποιηθεί ή όχι. Γι’αυτό είναι χρήσιμο να αντιστοιχίσουμε σε κάθε ενδεχόμενο Α έναν αριθμό, που θα είναι ένα μέτρο της “προσδοκίας” με την οποία αναμένουμε την πραγματοποίησή του. Τον αριθμό αυτό τον ονομάζουμε πιθανότητα του Α και τον συμβολίζουμε με P(Α). Πώς όμως θα προσδιορίσουμε για κάθε ενδεχόμενο ενός πειράματος τύχης την πιθανότητά του; Δηλαδή πώς θα βρούμε μια διαδικασία με την οποία σε κάθε ενδεχόμενο θα αντιστοιχίζουμε την πιθανότητά του; Θα προσπαθήσουμε στη συνέχεια να απαντήσουμε στα ερωτήματα αυτά.
Έννοια και Ιδιότητες Σχετικής Συχνότητας
Αν σε ν εκτελέσεις ενός πειράματος ένα ενδεχόμενο Α πραγματοποιείται κ φορές, τότε ο λόγος
![]() ονομάζεται σχετική συχνότητα του Α και συμβολίζεται με
ονομάζεται σχετική συχνότητα του Α και συμβολίζεται με
![]() . Ιδιαίτερα αν ο δειγματικός χώρος ενός πειράματος είναι το πεπερασμένο σύνολο Ω={ω1,ω2,...,ωλ} και σε ν εκτελέσεις του πειράματος αυτού τα απλά ενδεχόμενα {ω1},{ω2},...,{ωλ} πραγματοποιούνται {κ1},{κ2},...,{κλ} φορές αντιστοίχως, τότε για τις σχετικές συχνότητες
. Ιδιαίτερα αν ο δειγματικός χώρος ενός πειράματος είναι το πεπερασμένο σύνολο Ω={ω1,ω2,...,ωλ} και σε ν εκτελέσεις του πειράματος αυτού τα απλά ενδεχόμενα {ω1},{ω2},...,{ωλ} πραγματοποιούνται {κ1},{κ2},...,{κλ} φορές αντιστοίχως, τότε για τις σχετικές συχνότητες
![]() των απλών ενδεχομένων θα έχουμε:
των απλών ενδεχομένων θα έχουμε:
1. 0≤![]() ≤1, i=1,2,...,λ (αφού 0≤ κi≤ ν )
≤1, i=1,2,...,λ (αφού 0≤ κi≤ ν )
2. ![]() .
.
Ας εκτελέσουμε τώρα το ακόλουθο πείραμα: Ρίχνουμε ένα συμμετρικό και ομογενές νόμισμα και σημειώνουμε με Κ το αποτέλεσμα “κεφαλή” και με Γ το αποτέλεσμα “γράμματα”.
Στον παρακάτω πίνακα αναφέρονται το πλήθος των Κ και οι αντίστοιχες σχετικές συχνότητες στις 10, 20, 30,…,200 ρίψεις του νομίσματος ενώ στο σχήμα 1 παριστάνεται το αντίστοιχο διάγραμμα σχετικών συχνοτήτων
Πίνακας |
||
| ν | κ |
|
| 10 20 30 40 50 60 70 80 90 100 110 120 130 140 150 160 170 180 190 200 |
7 13 16 23 26 31 33 39 43 46 53 61 66 70 73 81 87 89 93 99 |
0,700 0,650 0,533 0,575 0,520 0,517 0,471 0,488 0,478 0,460 0,482 0,508 0,508 0,500 0,486 0,506 0,512 0,494 0,489 0,495 |
Διάγραμμα σχετικών συχνοτήτων
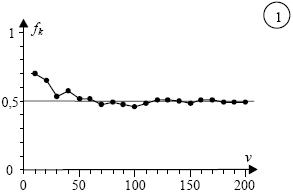
Παρατηρούμε ότι καθώς αυξάνεται ο αριθμός ν των ρίψεων η σχετική συχνότητα ![]() εμφάνισης της “κεφαλής” σταθεροποιείται γύρω από την τιμή 0,5 ή, όπως λέμε “τείνει” στον αριθμό 0,5. Αυτό επιβεβαιώνει την “προσδοκία” μας ότι στη ρίψη ενός συμμετρικού και ομογενούς νομίσματος ή, όπως λέμε, ενός “αμερόληπτου” νομίσματος, οι σχετικές συχνότητες των ενδεχομένων {K},{Γ} είναι ίσες. Ανάλογα παραδείγματα μας οδηγούν στο συμπέρασμα ότι οι σχετικές συχνότητες πραγματοποίησης των ενδεχομένων ενός πειράματος σταθεροποιούνται γύρω από κάποιους αριθμούς (όχι πάντοτε ίδιους), καθώς ο αριθμός των δοκιμών του πειράματος επαναλαμβάνεται απεριόριστα. Το εμπειρικό αυτό εξαγόμενο, το οποίο επιβεβαιώνεται και θεωρητικά, ονομάζεται στατιστική ομαλότητα ή νόμος των μεγάλων αριθμών.
εμφάνισης της “κεφαλής” σταθεροποιείται γύρω από την τιμή 0,5 ή, όπως λέμε “τείνει” στον αριθμό 0,5. Αυτό επιβεβαιώνει την “προσδοκία” μας ότι στη ρίψη ενός συμμετρικού και ομογενούς νομίσματος ή, όπως λέμε, ενός “αμερόληπτου” νομίσματος, οι σχετικές συχνότητες των ενδεχομένων {K},{Γ} είναι ίσες. Ανάλογα παραδείγματα μας οδηγούν στο συμπέρασμα ότι οι σχετικές συχνότητες πραγματοποίησης των ενδεχομένων ενός πειράματος σταθεροποιούνται γύρω από κάποιους αριθμούς (όχι πάντοτε ίδιους), καθώς ο αριθμός των δοκιμών του πειράματος επαναλαμβάνεται απεριόριστα. Το εμπειρικό αυτό εξαγόμενο, το οποίο επιβεβαιώνεται και θεωρητικά, ονομάζεται στατιστική ομαλότητα ή νόμος των μεγάλων αριθμών.
Θα προσπαθήσουμε τώρα στηριζόμενοι στις προηγούμενες διαπιστώσεις να ορίσουμε την πιθανότητα ενός ενδεχομένου.