2.1 ΟΙ ΠΡΑΞΕΙΣ ΚΑΙ ΟΙ ΙΔΙΟΤΗΤΕΣ ΤΟΥΣ (Επαναλήψεις – Συμπληρώσεις)
Εισαγωγή
Στο Γυμνάσιο μάθαμε ότι οι πραγματικοί αριθμοί αποτελούνται από τους ρητούς και τους άρρητους αριθμούς και παριστάνονται με τα σημεία ενός άξονα, του άξονα των πραγματικών αριθμών.
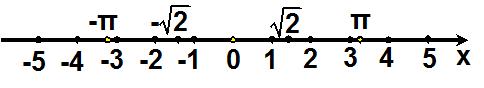
Θυμίζουμε ότι:
- Κάθε ρητός αριθμός έχει (ή μπορεί να πάρει) κλασματική μορφή, δηλαδή τη μορφή
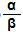 , όπου α, β ακέραιοι, με β ≠ 0.
, όπου α, β ακέραιοι, με β ≠ 0.
- Κάθε ρητός αριθμός μπορεί να γραφεί ως δεκαδικός ή περιοδικός δεκαδικός και, αντιστρόφως, κάθε δεκαδικός ή περιοδικός δεκαδικός μπορεί να πάρει κλασματική μορφή. Για παράδειγμα,
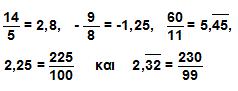
Μπορούμε δηλαδή να πούμε ότι οι ρητοί αριθμοί αποτελούνται από τους δεκαδικούς και τους περιοδικούς δεκαδικούς αριθμούς.
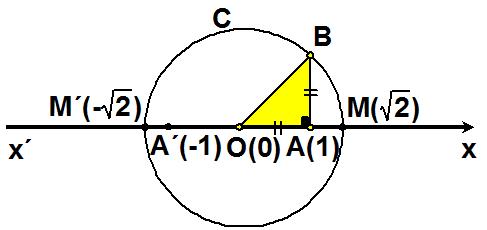
Υπάρχουν όμως και αριθμοί, όπως οι ![]() π, κτλ., που δεν μπορούν να πάρουν τη μορφή , όπου α, β
ακέραιοι, με β ≠ 0 (ή, με άλλα λόγια, δεν μπορούν να γραφούν ούτε ως δεκαδικοί ούτε ως περιοδικοί δεκαδικοί). Οι αριθμοί αυτοί λέγονται άρρητοι αριθμοί.
π, κτλ., που δεν μπορούν να πάρουν τη μορφή , όπου α, β
ακέραιοι, με β ≠ 0 (ή, με άλλα λόγια, δεν μπορούν να γραφούν ούτε ως δεκαδικοί ούτε ως περιοδικοί δεκαδικοί). Οι αριθμοί αυτοί λέγονται άρρητοι αριθμοί.
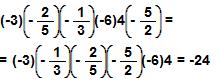
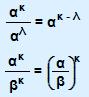
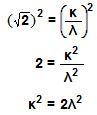
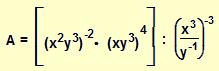
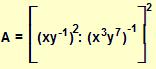 για x = 0,4 και y =
– 2,5.
για x = 0,4 και y =
– 2,5.