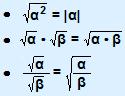2.4 ΡΙΖΕΣ ΠΡΑΓΜΑΤΙΚΩΝ ΑΡΙΘΜΩΝ

Τετραγωνική ρίζα μη αρνητικού αριθμού

Στο Γυμνάσιο μάθαμε την έννοια της τετραγωνικής ρίζας μη αρνητικού αριθμού και τις ιδιότητές της. Συγκεκριμένα μάθαμε ότι:

ΟΡΙΣΜΟΣ

H τετραγωνική ρίζα ενός μη αρνητικού αριθμού α συμβολίζεται με και είναι ο μη αρνητικός αριθμός που, όταν υψωθεί στο τετράγωνο, δίνει τον α.

Μπορούμε επομένως να πούμε ότι:
Αν α > 0, η παριστάνει τη μη αρνητική λύση της εξίσωσης x² = α .

Για τις τετραγωνικές ρίζες μη αρνητικών αριθμών γνωρίσαμε τις παρακάτω ιδιότητες:

ν–οστή ρίζα μη αρνητικού αριθμού

ΟΡΙΣΜΟΣ

Η ν–οστή ρίζα ενός μη αρνητικού αριθμού α συμβολίζεται με και είναι ο μη αρνητικός αριθμός(1) που, όταν υψωθεί στην ν, δίνει τον α.

Επίσης γράφουμε

Μπορούμε επομένως να πούμε ότι:
Αν α ≥ 0, τότε η παριστάνει τη μη αρνητική λύση της εξίσωσης x^ν = α .

ΣΧΟΛΙΟ
Είναι 10⁴ = 10000, οπότε = 10. Είναι επίσης και (–10)⁴ = 10000. Όμως, δεν επιτρέπεται να γράφουμε = –10, αφού, σύμφωνα με τον παραπάνω ορισμό, η είναι η μη αρνητική λύση της εξίσωσης x⁴ = 10000.

⁽¹⁾Αποδεικνύεται ότι υπάρχει και είναι μοναδικός

Ιδιότητες των ριζών

Από τον ορισμό της ν–οστής ρίζας ενός μη αρνητικού αριθμού α , συμπεραίνουμε αμέσως ότι:

— Αν α ≥ 0, τότε: — Αν α ≤ 0 και ν άρτιος, τότε:

Για παράδειγμα:

Ισχύουν όμως και οι ακόλουθες ιδιότητες, από τις οποίες οι δύο πρώτες είναι ανάλογες των ιδιοτήτων της τετραγωνικής ρίζας:

ΑΠΟΔΕΙΞΗ
1. Έχουμε:

, που ισχύει.

2. Αποδεικνύεται όπως και η 1.

3. Έχουμε:

4. Έχουμε:

ΣΧΟΛΙΟ
Η ιδιότητα 1. ισχύει και για περισσότερους από δυο μη αρνητικούς παράγοντες.
Συγκεκριμένα, για μη αρνητικούς αριθμούς α₁, α₂, ... , α_κ ισχύει:

Στην ειδική μάλιστα περίπτωση που είναι α₁ = α₂ = ... = α_κ = α > 0, ισχύει:

οπότε, λόγω της ιδιότητας 1, για α , β ≥ 0 έχουμε

Δυνάμεις με ρητό εκθέτη

Στη συνέχεια θα ορίσουμε παραστάσεις της μορφής α^μ/ν , όπου α > 0, μ ακέραιος και ν θετικός ακέραιος, τις οποίες θα ονομάσουμε δυνάμεις με ρητό εκθέτη. Ο ορισμός θα γίνει με τέτοιο τρόπο, ώστε να διατηρούνται οι γνωστές μας ιδιότητες των δυνάμεων με ακέραιο εκθέτη.
Τι θα πρέπει, για παράδειγμα, να σημαίνει το 3^2/5; Αν απαιτήσουμε να ισχύει η ιδιότητα και για δυνάμεις με ρητό εκθέτη, τότε θα είναι
Άρα πρέπει ο 3^2/5 να είναι λύση της εξίσωσης x⁵ = 3².
Δηλαδή πρέπει να είναι .
Γενικά:

ΟΡΙΣΜΟΣ

Επιπλέον, αν μ, ν θετικοί ακέραιοι, τότε ορίζουμε 0^μ/ν. Για παράδειγμα:

Με τη βοήθεια των ιδιοτήτων των ριζών αποδεικνύεται ότι οι ιδιότητες των δυνάμεων με ακέραιο εκθέτη ισχύουν και για δυνάμεις με ρητό εκθέτη. Το γεγονός αυτό διευκολύνει το λογισμό με τα ριζικά. Έτσι έχουμε για παράδειγμα είναι:

ΕΦΑΡΜΟΓΕΣ

1η Αν α και β είναι μη αρνητικοί αριθμοί, να αποδειχθεί η ισοδυναμία:

ΑΠΟΔΕΙΞΗ

Έχουμε:

<=> α < β , που ισχύει.

2η Να τραπούν οι παραστάσεις σε ισοδύναμες, χωρίς ριζικά στους παρονομαστές:

ΛΥΣΗ

Έχουμε:

3η Να αποδειχθεί ότι:

ΑΠΟΔΕΙΞΗ

Έχουμε:

Ασκήσεις

Α' ΟΜΑΔΑΣ
1.	Να υπολογίσετε τις ρίζες:
2.	Να γράψετε τις παρακάτω παραστάσεις χωρίς ριζικά
3.	Να αποδείξετε ότι:
4.	Να αποδείξετε ότι:
5.	Να αποδείξετε ότι:
6.	Να αποδείξετε ότι:
7.	Να αποδείξετε ότι:
8.	Να αποδείξετε ότι:
9.	Να αποδείξετε ότι:
10.	Να μετατρέψετε τις παρακάτω παραστάσεις σε ισοδύναμες με ρητούς παρανομαστές:
11.	Να αποδείξετε ότι: αφού αναλύσετε τα υπόριζα σε γινόμενα πρώτων παραγόντων.
B' ΟΜΑΔΑΣ
1.	i) Να αποδείξετε ότι: ii) Αν α, β > 0 να αποδείξετε ότι
2.	i) Να βρείτε τα αναπτύγματα των ii) Να αποδείξετε ότι:
3.	i) Να αποδείξετε ότι ο αριθμός είναι ρητός ii) Αν α θετικός ρητός, να αποδείξετε ότι οείναι ρητός.
4.	Να αποδείξετε ότι:
5.	Σε ένα ορθογώνιο τρίγωνο οι κάθετες πλευρές του είναι AB = και ΑΓ = i) Να υπολογίσετε την υποτείνουσα ΒΓ του τριγώνου. ii) Με τη βοήθεια της τριγωνικής ανισότητας να αποδείξετε ότι: < + iii) Για μη αρνητικούς αριθμούς α και β , να αποδείξετε ότι < + . Πότε ισχύει η ισότητα;

ΙΣΤΟΡΙΚΟ ΣΗΜΕΙΩΜΑ

Ο «διπλασιασμός του τετραγώνου», δηλαδή η κατασκευή ενός τετραγώνου με εμβαδόν διπλάσιο ενός άλλου δοθέντος τετραγώνου, μπορεί να γίνει με μια απλή «γεωμετρική» κατασκευή. Λέγοντας «γεωμετρική» κατασκευή εννοούμε κατασκευή με χάρακα και διαβήτη.

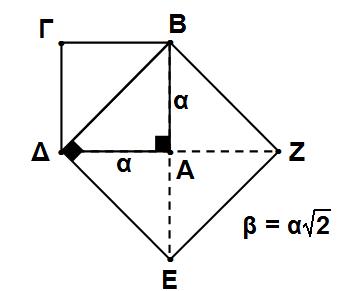
Ωστόσο, η πλευρά β, του τετραγώνου με το διπλάσιο εμβαδόν, δεν προκύπτει από την πλευρά α με πολλαπλασιασμό επί ρητό αριθμό. Αυτό σημαίνει ότι δεν υπάρχει ευθύγραμμο τμήμα (ως μονάδα μέτρησης) με το οποίο μπορούμε να μετρήσουμε ακριβώς τα δυο αυτά τμήματα, πλευρά και διαγώνιο τετραγώνου. Η απόδειξη της ύπαρξης άρρητων αριθμών θεωρείται μια από τις σπουδαιότερες ανακαλύψεις των Πυθαγορείων. (Πυθαγόρας: 6ος π. Χ. αιώνας). Οι αρχαίοι Έλληνες είχαν μια βαθιά πίστη ότι πάντοτε δυο ευθύγραμμα τμήματα έχουν κοινό μέτρο. Γι’ αυτό, στα πλαίσια της εποχής εκείνης, η ανακάλυψη αυτή των Πυθαγορείων δεν ήταν απλά και μόνο μια ενδιαφέρουσα μαθηματική πρόταση, αλλά σήμαινε την ανατροπή θεμελιωδών φιλοσοφικών αντιλήψεων για τον κόσμο και τη φύση.

Ήταν κεντρική αντίληψη των Πυθαγορείων ότι η ουσία κάθε όντος μπορεί να αναχθεί σε φυσικούς αριθμούς. Ο νεοπυθαγόρειος Φιλόλαος γύρω στα 450 π.Χ., έγραφε:

«Πραγματικά το καθετί που γνωρίζουμε έχει έναν αριθμό (δηλαδή φυσικό). Αλλιώς θα ήταν αδύνατο να το γνωρίσουμε και να το καταλάβουμε με τη λογική. Το ένα είναι η αρχή του παντός».

Η ανακάλυψη λοιπόν ότι υπάρχουν μεγέθη και μάλιστα απλά, όπως η υποτείνουσα τετραγώνου, τα οποία δεν μπορούν να εκφραστούν στα πλαίσια των φυσικών αριθμών, θεωρήθηκε αληθινή συμφορά για την πυθαγόρεια φιλοσοφία. Χαρακτηριστικοί είναι οι θρύλοι που περιβάλλουν το γεγονός αυτό. Κατά έναν από αυτούς, η ανακάλυψη της ύπαρξης των άρρητων αριθμών έγινε από τον πυθαγόρειο Ίπασσο, όταν αυτός και άλλοι Πυθαγόρειοι ταξίδευαν με πλοίο. Η αντίδραση των Πυθαγορείων ήταν να πνίξουν τον Ίπασσο και να συμφωνήσουν μεταξύ τους να μη διαδοθεί η ανακάλυψη προς τα έξω.

Η υπέρβαση των «δυσκολιών» που φέρνει στα Μαθηματικά η ύπαρξη άρρητων αριθμών, κατέστη δυνατή από τον Εύδοξο (360 π.Χ.) με την ιδιοφυή «θεωρία των Λόγων». Η απόδειξη για το ότι ένας συγκεκριμένος αριθμός είναι άρρητος είναι ένα πρόβλημα που απαιτεί πολλές φορές πολύπλοκούς συλλογισμούς.