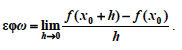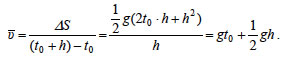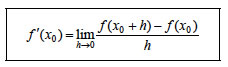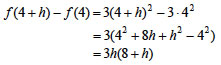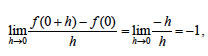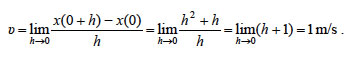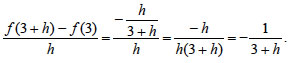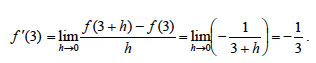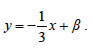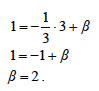1.2 Η ΕΝΝΟΙΑ ΤΗΣ ΠΑΡΑΓΩΓΟΥ

Εφαπτομένη Καμπύλης

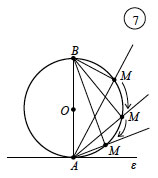
Εικόνα

Από τη Γεωμετρία γνωρίζουμε ότι η εφαπτομένη ενός κύκλου (O, R) σε ένα σημείο του Α είναι η ευθεία ε που είναι κάθετη στην ακτίνα ΟΑ στο σημείο Α. Έστω Μ ένα άλλο σημείο του κύκλου. Επειδή το τρίγωνο ΜΑΒ είναι ορθογώνιο στο Μ, το άθροισμα των γωνιών του Α και Β είναι 90°. Αν υποθέσουμε ότι το Μ κινούμενο πάνω στον κύκλο πλησιάζει το Α, η γωνία Β τείνει να γίνει μηδενική, οπότε η γωνία Α τείνει να γίνει ορθή. Δηλαδή η τέμνουσα ΑΜ τείνει να γίνει κάθετη στην ΟΑ που σημαίνει ότι τείνει να συμπέσει με την εφαπτομένη ε. Θα μπορούσαμε επομένως να ορίσουμε ως εφαπτομένη του κύκλου (O, R) στο σημείο Α, την οριακή θέση της τέμνουσας ΑΜ, καθώς το Μ κινούμενο πάνω στον κύκλο τείνει να συμπέσει με το Α.

Εικόνα

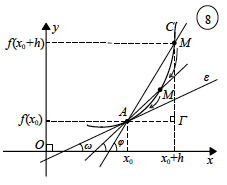
Τον ισοδύναμο αυτό ορισμό της εφαπτομένης ενός κύκλου θα τον χρησιμοποιήσουμε στη συνέχεια για να ορίσουμε την εφαπτομένη της γραφικής παράστασης μιας συνάρτησηςσε ένα σημείο της.
Έστω λοιπόν f μια συνάρτηση και Α(x0), f(x0)) ένα σημείο της γραφικής της παράστασης C.
Παίρνουμε και ένα άλλο σημείο Μ(x0 + h, f(x0 + h)) της C με h≠0.
Παρατηρούμε ότι καθώς το Μ κινούμενο πάνω στη C πλησιάζει το Α, όταν δηλαδή Εικόνα, τότε η ευθεία ΑΜ φαίνεται να παίρνει μια οριακή θέση ε η οποία λέγεται εφαπτομένη (tangent) της C στο Α. Από το σχήμα έχουμε ότι ο συντελεστής διεύθυνσης της ΑΜ είναι

Εικόνα


οπότε ο συντελεστής διεύθυνσης της εφαπτομένης της C στο Α θα είναι

Εικόνα

Στιγμιαία Ταχύτητα

Όπως έχει διαπιστωθεί πειραματικά από τον Γαλιλαίο πριν από τέσσερις αιώνες, το διάστημα S που διανύεται σε χρόνο t sec (s) από ένα σώμα που αφήνεταινα πέσει στο κενό εκφράζεταιαπό τον τύπο

Εικόνα


όπου Εικόνα είναι η σταθερή επιτάχυνση της βαρύτητας. Ποια όμως θα είναι η ταχύτητα ενός σώματος που πέφτει ελεύθερα σε ένα οποιοδήποτε σημείο της τροχιάς του, για παράδειγμα όταν t=5 s;
Μπορούμε να προσεγγίσουμε το ζητούμενο μέγεθος υπολογίζοντας τη μέση ταχύτητα σε ένα μικρό χρονικό διάστημα για παράδειγμα του ενός δεκάτου του δευτερολέπτου, από t=5 s στο t=5,1 s. Έχουμε:

Εικόνα


Ο πίνακας που ακολουθεί δείχνει τα αποτελέσματα όμοιων υπολογισμών της μέσης ταχύτητας για ολοένακαι μικρότερα χρονικά διαστήματα.

Εικόνα

Εικόνα

Φαίνεται ότι καθώς μικραίνει το χρονικό διάστημα, η μέση ταχύτητα πλησιάζει ολοένα και περισσότερο στην τιμή 49,05 m/s. Η οριακή αυτή τιμή των μέσων ταχυτήτων σε ολοένα και μικρότερα χρονικά διαστήματα με ένα άκρο το t=5 ορίζεται ως η στιγμιαία ταχύτητα του σώματος όταν t=5s. Έτσι η στιγμιαία ταχύτητα του σώματος ύστερα από χρόνο 5 s θα είναι υ=49,05 m/s.
Γενικότερα, ας υποθέσουμε ότι το σώμα ύστερα από t0 βρίσκεται στο σημείο Α και ας εξετάσουμε πόσο

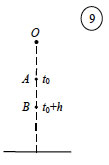
αυξάνεται το διανυόμενο διάστημα, όταν ο χρόνος αυξηθεί κατά h. Το κινητό διανύει σε χρόνο t0 διάστημα

Εικόνα


και σε χρόνο t0 + h διάστημα

Εικόνα


Άρα η αύξηση του διαστήματος σε χρόνο h είναι

Εικόνα


και η μέση ταχύτητα στο χρονικό διάστημα από t0 σε t0+h θα είναι

Εικόνα


Καθώς όμως ελαττώνεται το h πλησιάζοντας το μηδέν, χωρίς ποτέ να γίνεται ίσο με το μηδέν, η μέση ταχύτητα θα πλησιάζει όλο και περισσότερο στο gt0.
Την οριακή αυτή τιμή τη λέμε στιγμιαία ταχύτητα του κινητού στη χρονική στιγμή t0 ή απλώς ταχύτητα του κινητού στο t0.
Επομένως, η ταχύτητα υ του κινητού τη χρονική στιγμή t0 θα είναι

Εικόνα


Προφανώς όταν t0=5, τότε υ=9,81·5=49,05 m/s, τιμή την οποία προσεγγίσαμε και προηγουμένως με αριθμητικούς υπολογισμούς.
Την ίδια πορεία μπορούμε να ακολουθήσουμε και για τον υπολογισμό της ταχύτητας ενός κινητού το οποίο εκτελεί ευθύγραμμη κίνηση, στη γενικότερη περίπτωση που η τετμημένη του ή, όπως λέμε στη Φυσική, η θέση του τη χρονική στιγμή t εκφράζεται από τη συνάρτηση x=f(t).

Εικόνα


Για να βρούμε την ταχύτητα του κινητού τη χρονική στιγμή t0, θεωρούμε το χρονικό διάστημα από t0 έως t0+h με h≠0. Το κινητό σε χρόνο h μετατοπίζεται κατά Δx=x2-x1=f(t0+h)-f(t0).
Επομένως, η μέση ταχύτητα του κινητού στηδιάρκεια του χρονικού διαστήματος h θα είναι

Εικόνα


Αν σκεφτούμε όπως στην προηγούμενη ειδική περίπτωση, συμπεραίνουμε ότι η ταχύτητα του κινητού τη χρονική στιγμή t0 θα είναι

Εικόνα


Δηλαδή θα είναι το όριο του λόγου της μεταβολής της τετμημένης του κινητού προς την αύξηση του χρόνου, καθώς η τελευταία τείνει προς το μηδέν χωρίς στην πραγματικότητα να γίνεται ίση με το μηδέν.

Παράγωγος της f στο x=x0

Και τα δύο προηγούμενα προβλήματα, μολονότι αναφέρονται σε διαφορετικούς επιστημονικούς κλάδους, το πρώτο στη Γεωμετρία και το δεύτερο στη Μηχανική, οδηγούν στονυπολογισμό ενός ορίου της μορφής

Εικόνα


Υπάρχουν όμως και πολλά άλλα προβλήματα διαφορετικής φύσεως, όπως, για παράδειγμα, είναι ο ορισμός της έντασης ενός ρεύματος, της ταχύτητας μιας χημικής αντίδρασης, του οριακού κόστους στην Οικονομία, τα οποία οδηγούν στον υπολογισμό ενός ορίου της ιδίας μορφής.
Αν το προηγούμενο όριο υπάρχει και είναι πραγματικός αριθμός, τότε λέμε ότι η f είναι παραγωγίσιμη στο σημείο x0 του πεδίου ορισμού της. Το όριο αυτό ονομάζεται παράγωγος της f στο x0, συμβολίζεται με f '(x0) και διαβάζεται “f τονούμενο του x0”. Έχουμε λοιπόν:

Εικόνα


Για παράδειγμα, αν θέλουμε να υπολογίσουμε την παράγωγο της συνάρτησης f(x)=3x2 στο σημείο 4, εργαζόμαστε ως εξής:
  • Βρίσκουμε τη διαφορά f(4+h)-f(4):

    Εικόνα

  • Για h≠0, βρίσκουμε το πηλίκο Εικόνα

    Εικόνα


  • υπολογίζουμε το όριο Εικόνα

    Εικόνα


Άρα, f '(4)=24.

Η παράγωγος της f στο x0 εκφράζει το ρυθμό μεταβολής (rate of change) του y=f(x) ως προς το x, όταν 
x = x0. Έτσι, σύμφωνα με όσα εκθέσαμε στην προηγούμενη παράγραφο:

  • Ο συντελεστής διεύθυνσης της εφαπτομένης της καμπύλης που είναι η γραφική παράσταση μιας συνάρτησης f στο σημείο (x0, f(x0) θα είναι f '(x0), δηλαδή ο ρυθμός μεταβολής της f(x) ως προς x όταν x=x0.

  • Η ταχύτητα ενός κινητού που κινείται ευθύγραμμα και η θέση του στον άξονα κίνησής του εκφράζεται από τη συνάρτηση x=f(t) θα είναι τη χρονική στιγμή t0

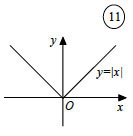
    Εικόνα


    δηλαδή ο ρυθμός μεταβολής της f(t) ως προς t όταν t=t0.

ΣΧΟΛΙΟ

Εικόνα

Υπάρχουν και συναρτήσεις οι οποίες δεν έχουν παράγωγο σε ένα σημείο. Όπως είναι, για παράδειγμα, η συνάρτηση f(x)=| x | στο x0 = 0. Διότι όταν h<0, έχουμε

Εικόνα


ενώ όταν h>0, έχουμε Εικόνα, που σημαίνει ότι δεν υπάρχει το Εικόνα.

ΕΦΑΡΜΟΓΕΣ

1. Η θέση ενός υλικού σημείου που εκτελεί ευθύγραμμη κίνηση εκφράζεται με τη συνάρτηση x(t) = t2 + t, όπου το t μετριέται σε δευτερόλεπτα.

α) Να βρεθεί η μέση ταχύτητα στα παρακάτω χρονικά διαστήματα:
(i) [0, 2]   (ii) [0, 1]   (iii) [0, 0,5]   (iv) [0, 0,1]

β) Να βρεθεί ηταχύτητα όταν t=0.

γ) Να σχεδιαστεί η γραφική παράσταση της συνάρτησης x=x(t).

δ) Να σχεδιαστούν οι τέμνουσες από το O(0, 0) της γραφικής παράστασης με συντελεστή διεύθυνσης τις μέσες ταχύτητες του ερωτήματος (α).

Επίσης, να βρεθεί και να σχεδιαστεί η εφαπτομένη της καμπύλης της συνάρτησης x=x(t) στο σημείο της με t=0.


ΛΥΣΗ

α) Από τον ορισμό της μέσης ταχύτητας έχουμε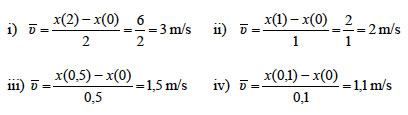
Εικόνα
β) Η ταχύτητα υ όταν t=0, είναι

Εικόνα


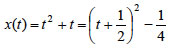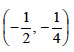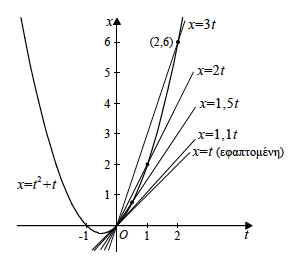
γ) Αν σε ένα ορθοκανονικό σύστημα ο οριζόντιος άξονας παριστάνει το χρόνο t και ο κατακόρυφος άξονας το x(t), τότε η γραφική παράσταση της συνάρτησης Εικόνα είναι, σύμφωνα με όσα γνωρίζουμε από την Α΄ Λυκείου, μια παραβολή με κορυφή το σημείο Εικόνα και άξονα συμμετρίας την ευθεία Εικόνα Έτσι, έχουμε την παρακάτω γραφική παράσταση.

Εικόνα


δ) Επειδή οι τέμνουσες διέρχονται από το σημείο O(0, 0) και έχουν συντελεστές διεύθυνσης 3, 2, 1,5 και 1,1, οι εξισώσεις τους είναι x=3t, x= 2t, x=1,5t και x=1,1t αντιστοίχως. Οι ευθείες αυτές έχουν σχεδιαστεί στο παραπάνω σχήμα.

Η εφαπτομένη της καμπύλης στο σημείο της με t=0 θα έχει συντελεστή διεύθυνσης ίσο με τη στιγμιαία ταχύτητα όταν t=0, δηλαδή ίσο με 1. Επειδή η εφαπτομένη αυτή διέρχεται και από την αρχή των αξόνων, η εξίσωσή της είναι x=t, δηλαδή είναιη διχοτόμοςτηςγωνίας των θετικών ημιαξόνων.

2. Δίνεται η συνάρτηση Εικόνα
i) Να βρεθεί η f '(3).
ii) Να βρεθεί η εξίσωση της εφαπτομένης της καμπύλης της f στο σημείο της (3, f (3)) και να σχεδιαστεί η εφαπτομένη αυτή.


ΛΥΣΗ

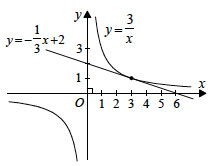
i) Έχουμε Εικόνα και για h≠0

Εικόνα


Επομένως

Εικόνα

Εικόνα

ii) Η εφαπτομένη της καμπύλης της f στο σημείο της με x=3 έχει συντελεστή διεύθυνσης ίσο με f '(3). Επομένως, η εξίσωσή της είναι

Εικόνα


Επειδή όμως το σημείο (3, f(3))=(3, 1) ανήκει στην εφαπτομένη, έχουμε

Εικόνα


Άρα, η εξίσωση της εφαπτομένης είναι 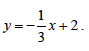Εικόνα

Ασκήσεις

Α' ΟΜΑΔΑΣ
1.

Να βρείτε την παράγωγο της συνάρτησης
i) f(x)=3x + 1 στο x=3
ii) g(x)=x 2+ 5 στο x=-2
iii) σ(x)=x2 + 2x στο x=4

2.

Να βρείτε την παράγωγο της συνάρτησης Εικόνα στο t=1.

3. i) Το μήκος L ενός κύκλου ακτίνας r είναι L=2πr. Να βρείτε το ρυθμό μεταβολής του L ως προς r, όταν r=3.
ii) Το εμβαδόν Ε ενός κύκλου ακτίνας r είναι E=πr2. Να βρείτε το ρυθμό μεταβολής του Ε ως προς r, όταν r=2.
4. i) Να βρείτε το ρυθμό μεταβολής του εμβαδού Ε ενός τετραγώνου πλευράς x ως προς x όταν x=5.
ii) Να βρείτε το ρυθμό μεταβολής του όγκου ενός κύβου πλευράς x ως προς x, όταν x=10 .
5. Να βρείτε την εξίσωση της εφαπτομένης της γραφικής παράστασης της συνάρτησης:
i) f(x)=x2 στο Α(3, f(3))
ii) f(x)=2√x, στο Α(4, f(4))