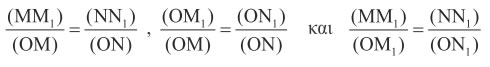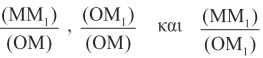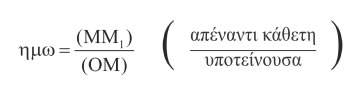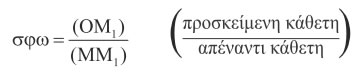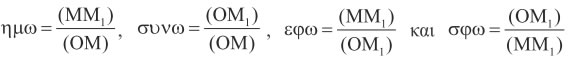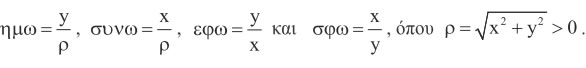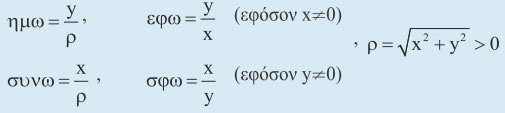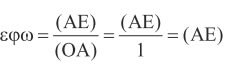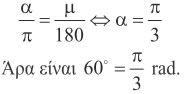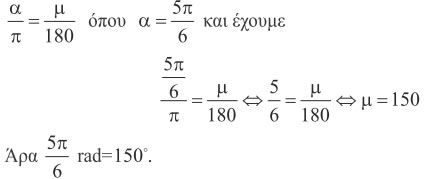|
3.1 ΤΡΙΓΩΝΟΜΕΤΡΙΚΟΙ ΑΡΙθΜΟΙ ΓΩΝΙΑΣ Τριγωνομετρικοί αριθμοί οξείας γωνίας | |
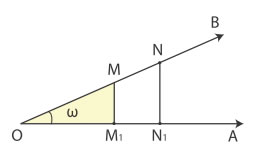
Έστω οξεία γωνία ω. Αν πάνω στη μία από τις δύο πλευρές της γωνίας
πάρουμε τυχαία σημεία Μ και Ν και φέρουμε τις κάθετες MM1 και
NN1 προς την άλλη πλευρά της γωνίας, τότε τα τρίγωνα 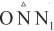 θα είναι
όμοια, οπότε θα ισχύει: θα είναι
όμοια, οπότε θα ισχύει: |
 |
|
Επομένως, για τη γωνία ω τα πηλίκα
είναι σταθερά, δηλαδή ανεξάρτητα της θέσης του σημείου Μ πάνω στην πλευρά της γωνίας. Τα πηλίκα αυτά, όπως γνωρίζουμε από Γυμνάσιο, ονομάζονται ημίτονο, συνημίτονο και εφαπτομένη της γωνίας ω και συμβολίζονται με ημω, συνω και εφω, αντιστοίχως. Δηλαδή, στο ορθογώνιο τρίγωνο
| |
|
Ορίζουμε ακόμα ως συνεφαπτομένη της οξείας γωνίας ω, την οποία συμβολίζουμε με σφω, το σταθερό πηλίκο
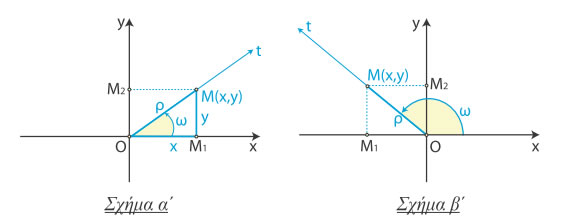
Πάνω στην τελική πλευρά της γωνίας ω παίρνουμε τυχαίο σημείο Μ(x, y)
και φέρνουμε την κάθετη MM1
Όμως (ΟM1) = x , (MM1) = y και οι παραπάνω ισότητες γράφονται :
|
|
Γενικεύοντας τα παραπάνω, ορίζουμε με τον ίδιο τρόπο τους
τριγωνομετρικούς αριθμούς οποιασδήποτε γωνίας ω (Σχήμα β΄). Σε κάθε λοιπόν
περίπτωση έχουμε :
όπου (x, y) οι συντεταγμένες οποιουδήποτε σημείου Μ (διαφορετικού του
Ο) της τελικής πλευράς της γωνίας ω και
Τριγωνομετρικοί αριθμοί γωνιών μεγαλύτερων των 360o και αρνητικών γωνιών | |
|
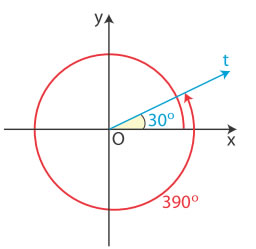
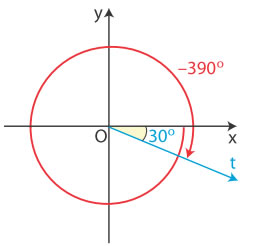
Ας υποθέσουμε ότι ο ημιάξονας Ox ενός συστήματος συντεταγμένων Oxy περιστρέφεται γύρω από το Ο κατά τη θετική φορά. Αν πραγματοποιήσει μια πλήρη περιστροφή και περιστραφεί επιπλέον και κατά γωνία μέτρου 30o , τότε λέμε ότι ο Ox έχει διαγράψει γωνία ω = 360o + 30o = 390o.
ω = v∙360o + μo = 390
όπου ν∈ N * και 0o ≤ μ ≤ 360o ω = ‒( 360o + 30o) = ‒390o. |
|
 | |
|
Με ανάλογο τρόπο ορίζονται οι αρνητικές γωνίες δηλαδή οι γωνίες της μορφής : ω = ‒( v∙360o + μo) = ‒390o, όπου ν∈ N και 0o≤ μ ≤ 360o Οι τριγωνομετρικοί αριθμοί γωνιών που είναι μεγαλύτερες από 360o , καθώς και των αρνητικών γωνιών,
ορίζονται όπως και οι τριγωνομετρικοί αριθμοί γωνιών από 0o μέχρι 360o
όπου (x, y) οι συντεταγμένες οποιουδήποτε σημείου Μ της τελικής πλευράς
της γωνίας ω (διαφορετικού του Ο) και Ας θεωρήσουμε τώρα μια γωνία ω (θετική ή αρνητική) με αρχική πλευρά τον
ημιάξονα Ox .Αν ο ημιάξονας Ox , στρεφόμενος γύρω από το Ο κατά τη θετική
φορά, συμπληρώσει ν πλήρεις στροφές και στη συνέχεια διαγράψει τη γωνία ω,
τότε θα έχει διαγράψει γωνία v∙360o + ω που έχει την
ίδια τελική πλευρά με την ω. Επομένως, για κάθε k ∈ Ζ θα ισχύει :
|
|
Ο τριγωνομετρικός κύκλος
| |
|
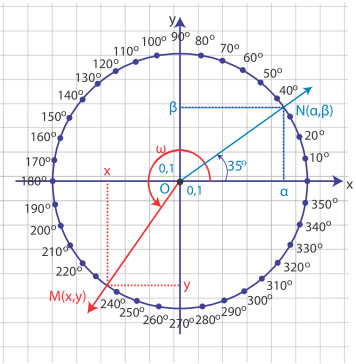
Με κέντρο την αρχή Ο(0,0) ενός συστήματος συντεταγμένων και ακτίνα ρ=1
γράψουμε έναν κύκλο. Ο κύκλος αυτός λέγεται τριγωνομετρικός
κύκλος. Επειδή ηµ35o = β/ρ και
ρ = 1 Ομοίως, επειδή συν35o = α/ρ
και ρ = 1 , |
|
|
Γενικότερα, αν η τελική πλευρά μιας γωνίας ω τέμνει τον τριγωνομετρικό κύκλο στο σημείο Μ(x, y), τότε ισχύει:
Για το λόγο αυτό ο άξονας x'x λέγεται και άξονας των συνημίτονων, ενώ ο
άξονας y'y λέγεται και άξονας των ημίτονων.
| |||
|
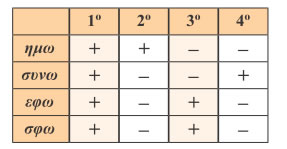
2. Τα πρόσημα των τριγωνομετρικών αριθμών μιας γωνίας ω, ανάλογα με το τεταρτημόριο στο οποίο βρίσκεται η τελική πλευρά της γωνίας αυτής, είναι όπως δείχνει ο παρακάτω πίνακας.
|
|
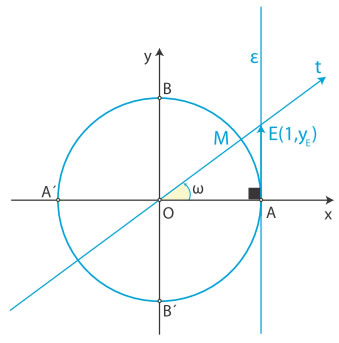
Ο άξονας των εφαπτομένων
|
 | |||
|
Αν με yE παραστήσουμε την τεταγμένη του Ε, τότε θα ισχύει (AE) = yE , οπότε θα είναι εφω = yE . Στο ίδιο συμπέρασμα καταλήγουμε και όταν η τελική πλευρά της γωνίας ω βρίσκεται σε οποιοδήποτε άλλο τεταρτημόριο. Επομένως σε κάθε περίπτωση ισχύει: εφω = yE =τεταγμένη του σημείου Ε Για το λόγο αυτό η ευθεία ε, που έχει εξίσωση x =1 , λέγεται άξονας των εφαπτομένων. | ||||
|
Το ακτίνιο ως μονάδα μέτρησης γωνιών Έχουμε γνωρίσει στο Γυμνάσιο το ακτίνιο ως μονάδα μέτρησης τόξων.
Συγκεκριμένα, ένα τόξο |
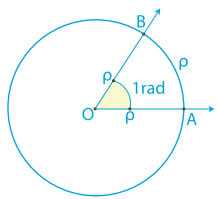 | |||
Από τον ορισμό αυτό προκύπτει και η σχέση μοίρας και ακτινίου ως μονάδων μέτρησης γωνιών, ως εξής : Έστω ότι μια γωνία ω είναι µo, και α rad . Επειδή το μήκος ενός κύκλου ακτίνας ρ είναι 2πρ , η γωνία 360o είναι ίση με 2π rad. οπότε , η γωνία 1 rad είναι ίση με 360/2π μοίρες , Επομένως , η γωνία α rad είναι ίση με α∙180/π μοίρες . Επειδή όμως η γωνία ω είναι µo , θα ισχύει µ = α∙180/π , οπότε θα έχουμε:
Για παράδειγμα : ✔ Για να εκφράσουμε τη γωνία 60o σε ακτίνια, θέτουμε στον τύπο α/π = μ/180 όπου μo = 60 0 και έχουμε
| ||||
|
✔ Για να τη γωνία 5π/6 rad σε μοίρες, θέτουμε στον τύπο
Στον παρακάτω πίνακα επαναλαμβάνουμε τους τριγωνομετρικούς αριθμούς μερικών γωνιών που είχαμε υπολογίσει στο Γυμνάσιο και οι οποίοι είναι ιδιαίτερα χρήσιμοι στις διάφορες εφαρμογές.
ΣΗΜΕΙΩΣΗ | ||||
|
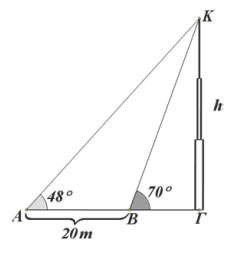
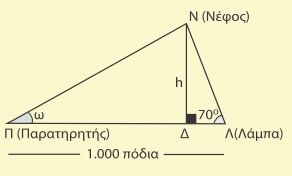
ΕΦΑΡΜΟΓΕΣ 1η οι μετρήσεις που έκανε ένας
μηχανικός για να βρει το ύψος h ενός καμπαναριού ΓΚ, φαίνονται στο διπλανό σχήμα. Να υπολογιστεί το ύψος του καμπαναριού σε μέτρα με προσέγγιση ακέραιας μονάδας. ΛΥΣΗ
2η Να υπολογιστούν οι τριγωνομετρικοί αριθμοί γωνίας 750o . ΛΥΣΗ
3η Να υπολογιστούν οι τριγωνομετρικοί αριθμοί γωνίας 79π/3 rad. ΛΥΣΗ
|
ΑΣΚΗΣΕΙΣ
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||