3.1 Εξισώσεις 1ου βαθμού

Εξισώσεις 1ου βαθμού

Α. Βοηθητικά στοιχεία			B. Ασκήσεις
1. Διερεύνηση της αx = β - Mεθοδολογία			Πακέτα λυμένων ασκήσεων , για εμπέδωση της θεωρίας 1. Ασκήσεις ανάπτυξης 2 . Ασκήσεις Σωστό- Λάθος 3 . Ασκήσεις πολλαπλής επιλογής 4 . Ασκήσεις Αντιστοίχισης 5 . Ασκήσεις Διάταξης 6 . Ασκήσεις συμπλήρωσης κενού

Γ. Εφαρμογές
Η εξίσωση αx + β = κx + λ Δώστε τα δύο μέλη μιας εξίσωσης ως παραστάσεις του αγνώστου x , και δείτε πως την λύνουμε βήμα προς βήμα Στη συνέχεια , δείτε και την λύση της , αν υπάρχει , στο άξονα x΄x.

Πρόβλημα 1α - Η εξίσωση \|x - α \| = β Η επίλυση της εξίσωσης \|x - α\| = β , με την βοήθεια του κύκλου. Η εφαρμογή διαθέτει ορισμένα εργαλεία και ζητά από τον μαθητή να βρεί τις λύσεις της παραπάνω εξίσωσης γεωμετρικά.

Πρόβλημα 1β - Η εξίσωση \|x - α \| = β Η επίλυση της εξίσωσης \|x - α\| = β , ''σαρώνοντας'' όλες τις πραγματικές τιμές της μεταβλητής x.

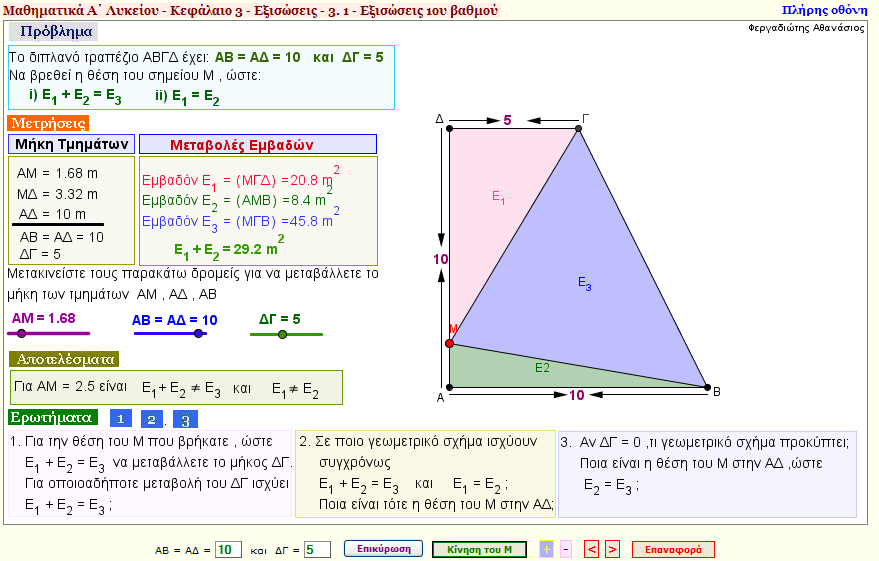
Πρόβλημα 2 Στο διπλανό σχήμα να βρεθεί η θέση του σημείου Μ , ώστε: i) E₁ + E₂ = E₃ ii) E₁ = E₂

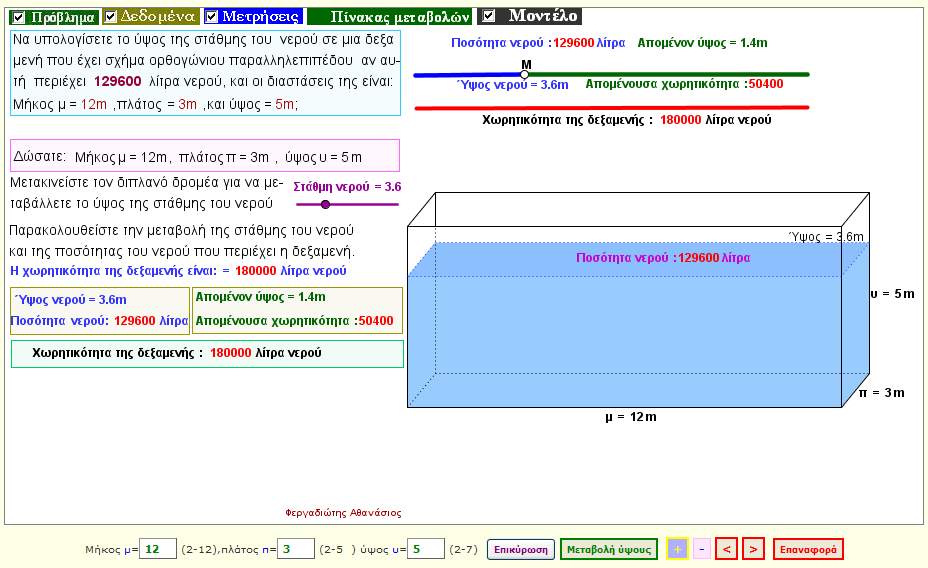
Πρόβλημα 3 Να υπολογίσετε το ύψος της στάθμης του νερού στη διπλανή δεξαμενή (που είναι ορθογώνιο παραλληλεπίπεδο) με διαστάσεις: Μήκος μ , Πλάτος π και Ύψος υ

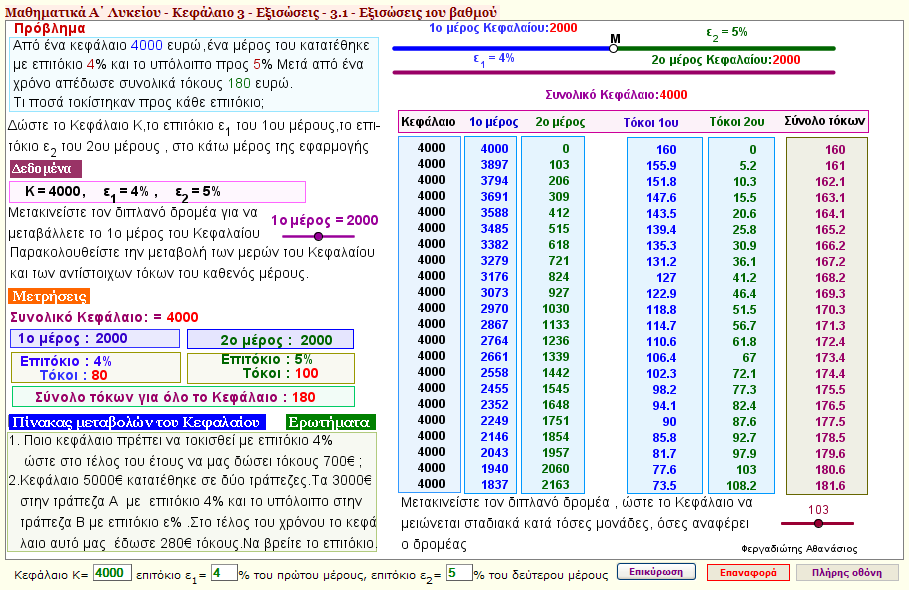
Πρόβλημα 4 Από ένα κεφάλαιο K ευρώ , ένα μέρος του κατατέθηκε με επιτόκιο ε_1 % και το υπόλοιπο προς ε_2 %. Μετά από ένα χρόνο απέδωσε συνολικά τόκους Τ ευρώ. Τι ποσά τοκίστηκαν προς κάθε επιτόκιο;

Πρόβλημα 5 Ποιοί περιορισμοί πρέπει να ισχύουν για τα α , β $\in R$ , ώστε να έχει λύση η εξίσωση $ \frac{x}{\alpha} +\frac{y}{β} $ = 1;

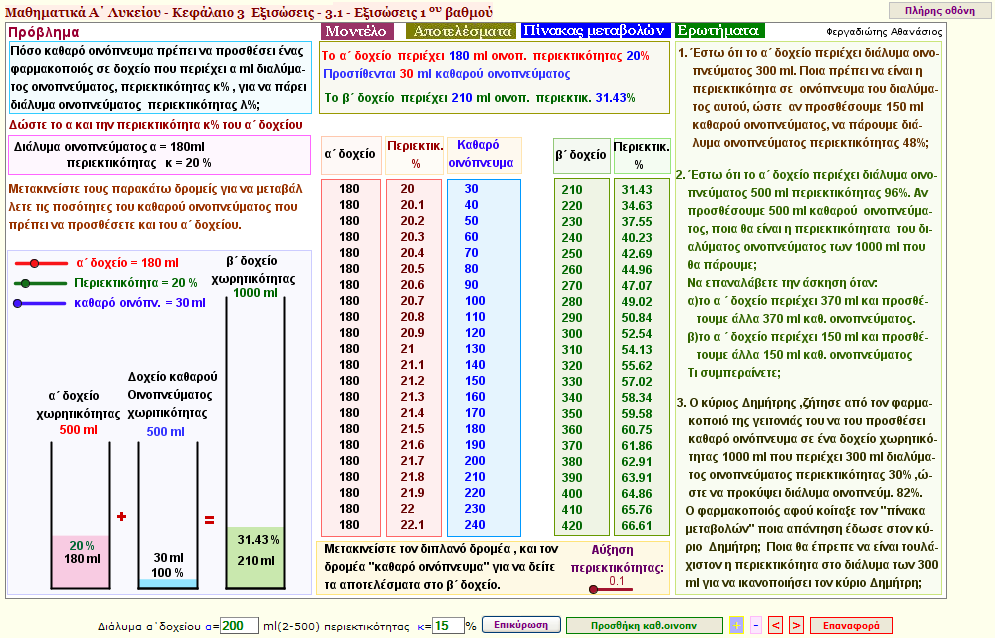
Πρόβλημα 6 Πόσο καθαρό οινόπνευμα πρέπει να προσθέσει ένας φαρμακοποιόςσε δοχείο που περιέχει α ml οινοπνεύματος, περιεκτικότητας κ% , για να πάρει οινόπνευμα περιεκτικότητας λ%;

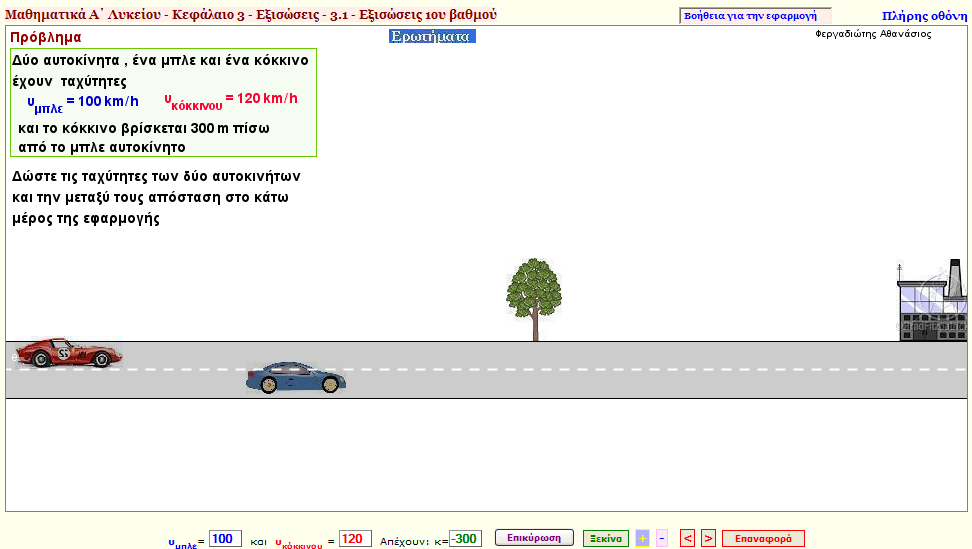
Πρόβλημα 7 Ένα αυτοκίνητο Α κινείται με ταχύτητα 100km/h. Ένα δεύτερο αυτοκίνητο Β που κινείται με 120km/h προσπερνάει το Α. Σε πόσα λεπτά τα δύο αυτοκίνητα θα απέχουν 1 km; Nα απαντήσετε επίσης και στις ερωτήσεις της εφαρμογής.

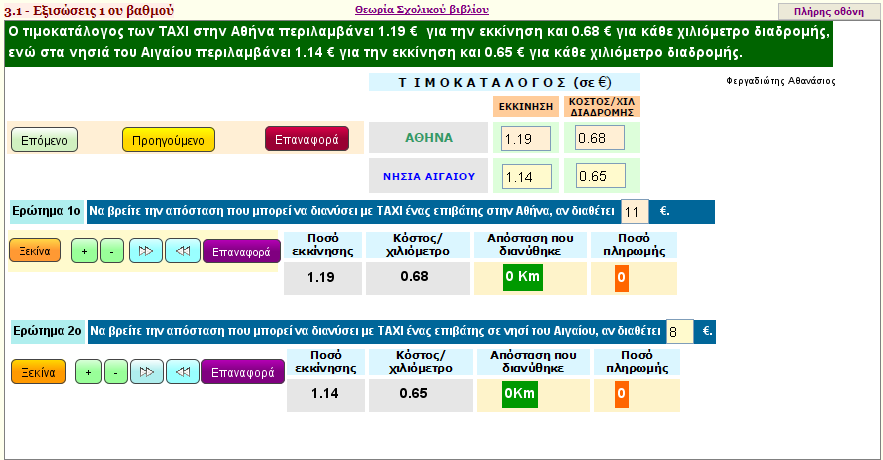
Δραστηριότητα 12 ΑΠΣ Ο τιμοκατάλογος των ΤΑΧΙ στην Αθήνα περιλαμβάνει 1,19? για την εκκίνηση και 0,68? για κάθε χιλιόμετρο διαδρομής, ενώ στα νησιά του Αιγαίου περιλαμβάνει 1,14? για την εκκίνηση και 0,65? για κάθε χιλιόμετρο διαδρομής. α) Να βρείτε την απόσταση που μπορεί να διανύσει με ΤΑΧΙ ένας επιβάτης στην Αθήνα, αν διαθέτει 10?. β) Να βρείτε την απόσταση που μπορεί να διανύσει με ΤΑΧΙ ένας επιβάτης σε νησί του Αιγαίου, αν διαθέτει 10?. γ) Αν στους νομούς της Θεσσαλίας η χρέωση για το ΤΑΧΙ περιλαμβάνει 2λ? για την εκκίνηση και λ? για κάθε χιλιόμετρο διαδρομής, να βρείτε σε σχέση με το λ την απόσταση που μπορεί να διανύσει ένας επιβάτης αν διαθέτει 10 ?. Αν στο νομό Λαρίσης η χρέωση ανά χιλιόμετρο διαδρομής είναι 0,60? και στο νομό Μαγνησίας 0,62?, να υπολογίσετε την απόσταση που μπορεί να διανύσει με ΤΑΧΙ ένας επιβάτης που διαθέτει 10?. Στόχος: Αναγνωρίζουν το ρόλο της παραμέτρου σε μία παραμετρική εξίσωση 1^ου βαθμού.