1.4 Συντεταγμένες στο επίπεδο

1.4 Συντεταγμένες στο επίπεδο
Α. Θεωρία			Β. Ασκήσεις
Πακέτο θεωρίας βιβλίου			Ασκήσεις ανάπτυξης
			Ασκήσεις αντιστοίχισης
			Ασκήσεις πολλαπλής επιλογής
			Ασκήσεις Σωστό - Λάθος
			Ασκήσεις διάταξης
			Ασκήσεις συμπλήρωσης κενού

			Ασκήσεις σχολικού βιβλίου
Γ. Εφαρμογές

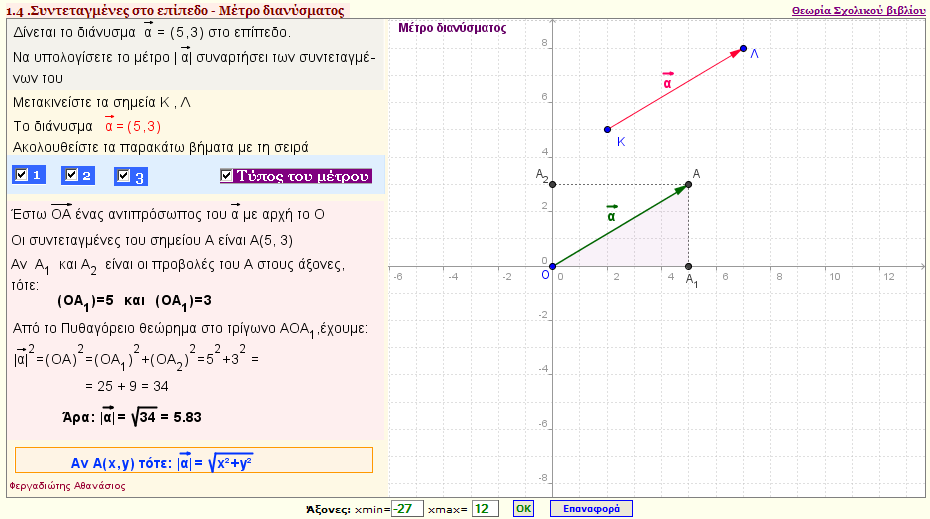
Μέτρο διανύσματος Δώστε ένα διάνυσμα ΚΛ και βρείτε το μέτρο του διανύσματος.Βρείτε τον τύπο του μέτρου του διανύσματος, αν $ \vec{KΛ}=(x,y) $

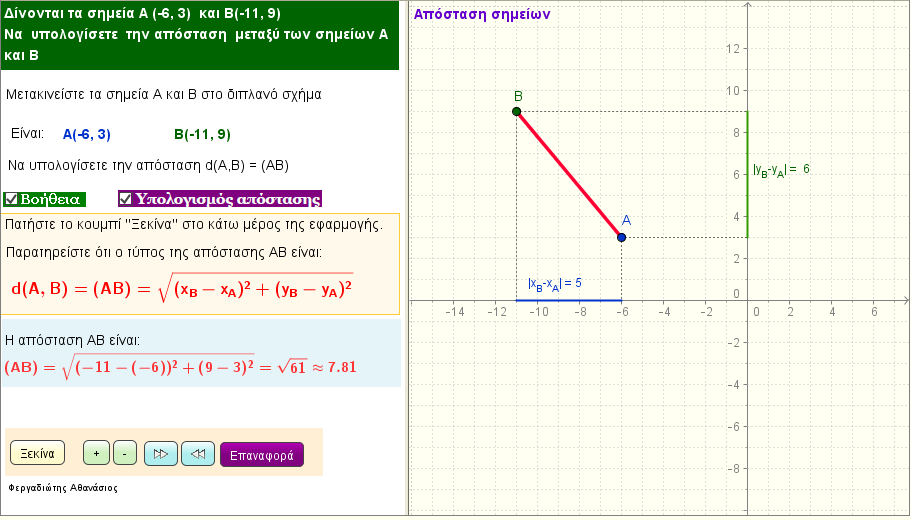
Απόσταση σημείων Δώστε δύο σημεία Α και Β και βρείτε την μεταξύ τους απόσταση

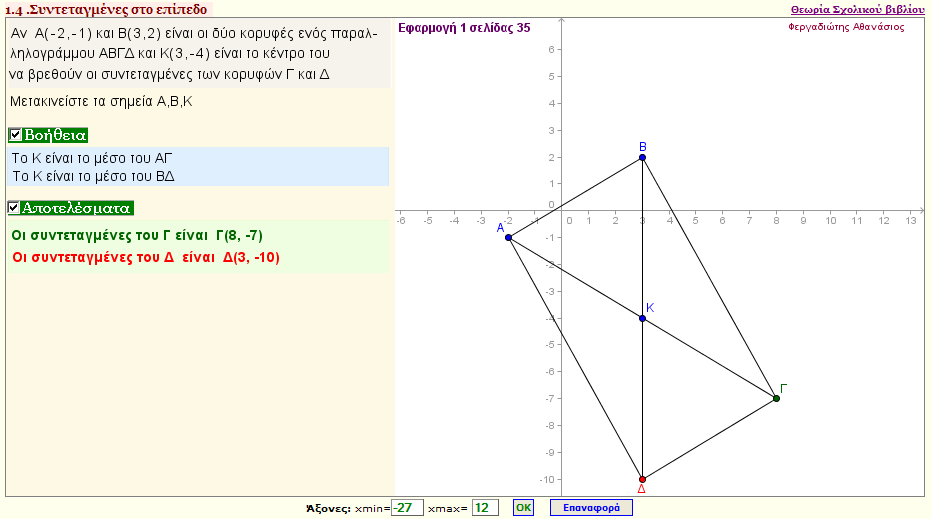
Eφαρμογή 1 Αν Α(x₁,y₁) και Β(x₂,y₂) είναι οι δύο κορυφές του παραλληλογράμμου ΑΒΓΔ και Κ(α,β) το κέντρο του , να βρεθούν oι συντεταγμένες των κορυφών Γ και Δ. (Τα x₁,y₁,x₂,y₂ ,α,β θεωρούνται γνωστά).

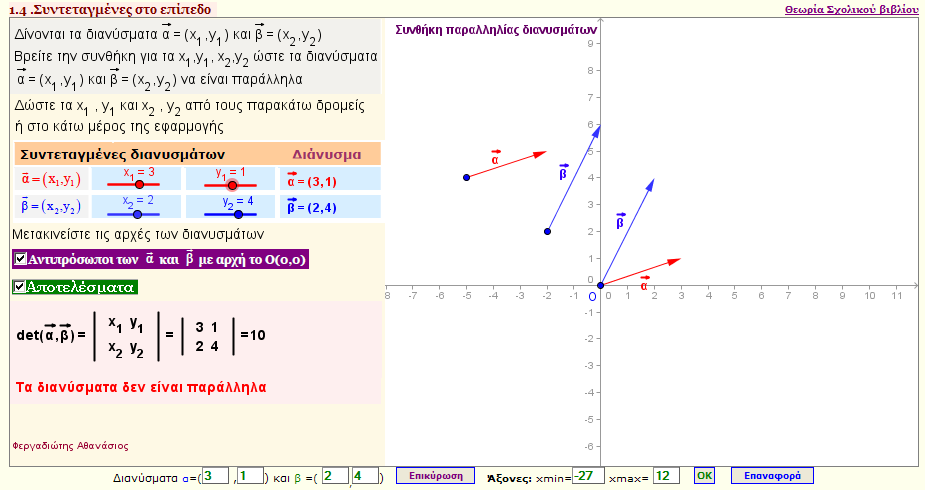
Συνθήκη παραλληλίας διανυσμάτων Αν $\vec{α}$=(x₁,y₁) και $\vec{β}$ = (x₂,y₂) , ποια σχέση πρέπει να συνδέι τα x₁,y₁,x₂,y₂,ώστε τα διανύσματα να είναι παράλληλα;

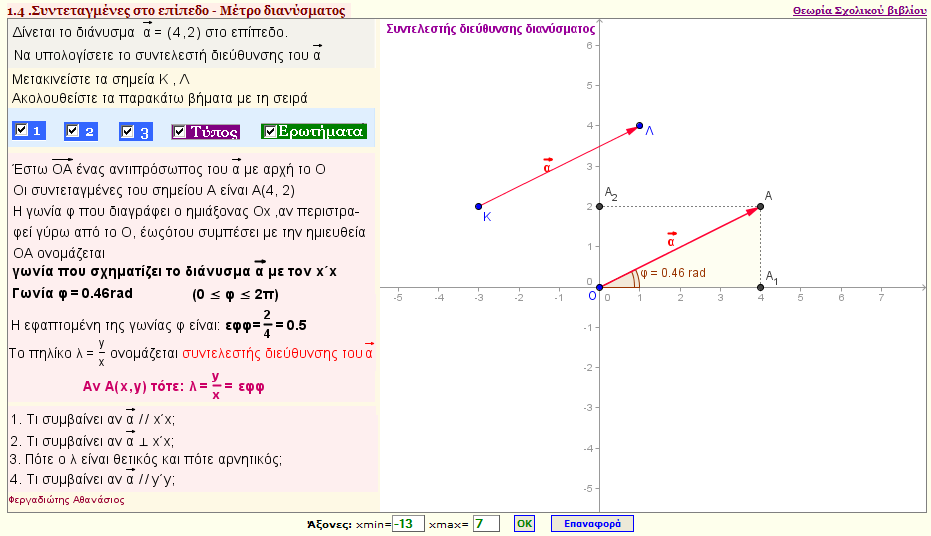
Συντελεστής διεύθυνσης διανύσματος Αν $\vec{α}$=(x₁,y₁) , τότε πως ορίζεται ο συντελεστής διεύθυνσης του διανύσματος; Ποιος είναι ο τύπος για τον συντελεστή του διανύσματος;

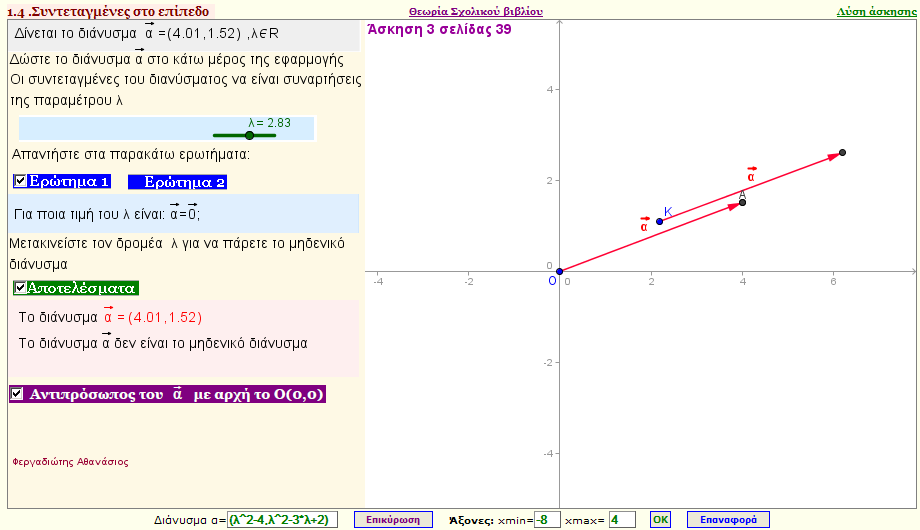
Πρόβλημα 1 Δίνεται το διάνυσμα $\vec{α}$=(λ²-4 ,λ²-3λ+2) .Για ποια τιμή του λ είναι: ι) $ \vec{α}= $ \vec{o} $; ii) $ \vec{α}\neq$ $ $ \vec{o} και $\vec{α}$//x΄x; (Mπορείτε να δώσετε για τις συντεταγμένες του $\vec{α}$ οποιαδήποτε συνάρτηση του λ

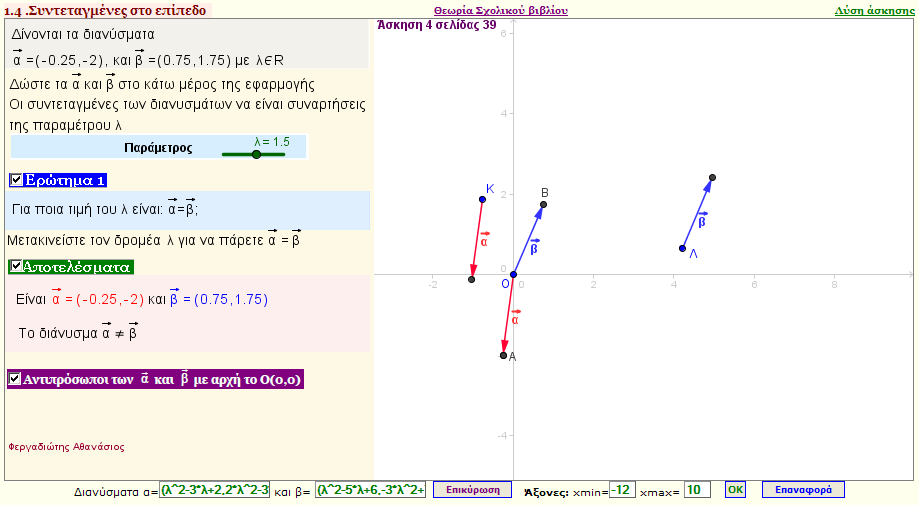
Πρόβλημα 2 Δίνεται το διάνυσμα $\vec{α}$=(λ²-3λ+2 ,2λ²-3λ-2) και $\vec{β}$=(λ²-5λ+6 ,-3λ²+7λ-2) .Για ποια τιμή του λ είναι: $ \vec{α}= $\vec{β} $; (Mπορείτε να δώσετε για τις συντεταγμένες του $\vec{α}$ οποιαδήποτε συνάρτηση του λ

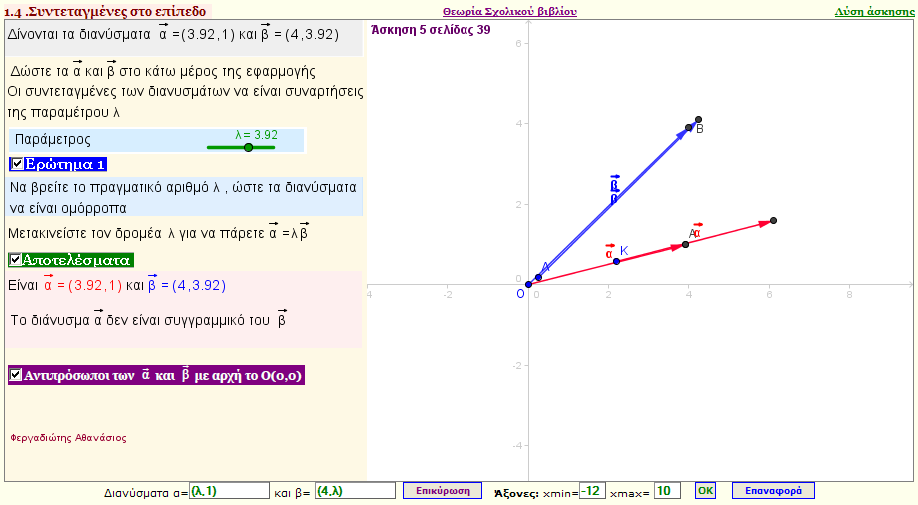
Πρόβλημα 3 Να βρείτε τον πραγματικό αριθμό λ , ώστε τα διανύσματα $\vec{α}$=(λ ,1) και $\vec{β}$=(4 ,λ) να είναι ομόρροπα. (Mπορείτε να δώσετε για τις συντεταγμένες του $\vec{α}$ οποιαδήποτε συνάρτηση του λ

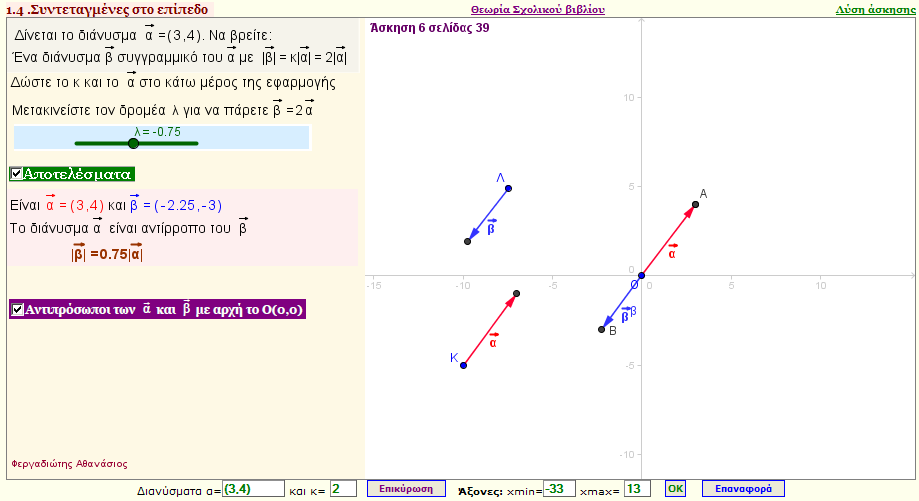
Πρόβλημα 4 Αν $\vec{α}$=(3 ,4) ποιο διάνυσμα είναι συγγραμμικό με το $ \vec{α} $ και έχει κ-πλάσιο μέτρο από $ \vec{α} $; (Mπορείτε να δώσετε οποιεσδήποτε συντεταγμένες για το διάνυσμα $\vec{α}$ και οποιονδήποτε θετικό αριθμό κ)

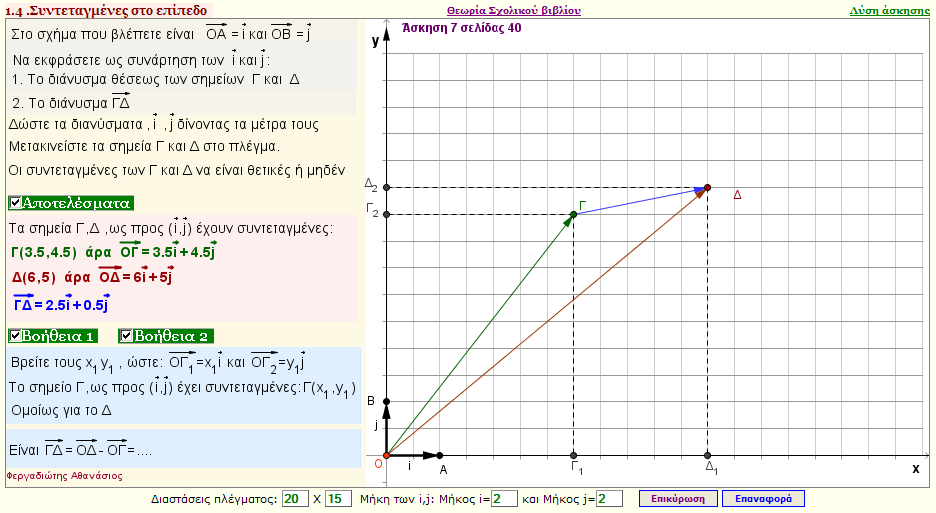
Πρόβλημα 5 Δίνεται σύστημα με βάση τα διανύσματα $\vec{i}$ και $\vec{j}$ .Δίνονται και δύο σημεία Γ , Δ του επιπέδου Να εκράσετε ως προς $ (\vec{i}, $\vec{j} $), τα διανύσματα $\vec{ΟΓ}$ και $\vec{ΟΔ}$ Στη συνέχεια να βρείτε το διάνυσμα $\vec{ΓΔ}$ (Mπορείτε να δώσετε οποιαδήποτε μήκη στα $\vec{i}$ και $\vec{j}$)

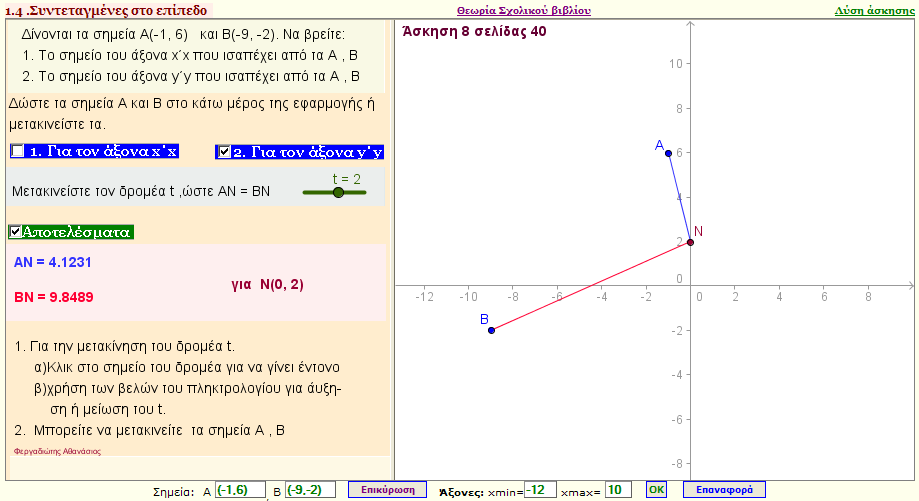
Πρόβλημα 6 Δίνονται τα σημεία Α(-1,6) και Β(-9,-2). Να βρείτε : ι) Το σημείο του άξονα x΄x που ισαπέχει από τα σημεία Α , Β ι) Το σημείο του άξονα y΄y που ισαπέχει από τα σημεία Α , Β (Mπορείτε να δώσετε οποιεσδήποτε συντεταγμένες στα σημεία Α , Β)