Ανδρέας Ιωάννου Κασσέτας

Το ΠΡΟΒΛΗΜΑ Φυσικής και η οικοδόμησή του

Ένα δομημένο εννοιακό σύνολο με δεδομένα και με ζητούμενα για να μπορεί να θεωρηθεί

«ΠΡΟΒΛΗΜΑ ΦΥΣΙΚΗΣ», απαιτείται

α . να είναι έτσι διατυπωμένο που να απαιτείται η μερική ή ολική ΜΕΤΑΦΡΑΣΗ του σε γλώσσα Φυσικής

β. οι δρόμοι της σκέψης να μην είναι άμεσα ορατοί αλλά να χρειάζεται να αναζητηθούν. Αυτό σημαίνει - εκτός των άλλων - ότι οι ΕΝΝΟΙΕΣ που θα χρησιμοποιηθούν και οι ΝΟΜΟΙ που θα εφαρμοστούν δεν υπάρχουν στο σύνολό τους στη διατύπωση

γ. τα ΦΑΙΝΟΜΕΝΑ πάνω στα οποία οικοδομείται και οι ΝΟΜΟΙ που απαιτούνται για τη λύση του να ανήκουν σε διάφορες περιοχές της Φυσικής.

Το φαινόμενο ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ και το φαινόμενο DOPPLER

Το φαινόμενο ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ κέντρου μάζας και το φαινόμενο ΚΥΛΙΣΗ

Το φαινόμενο ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ και το φαινόμενο ΚΡΟΥΣΗ

Το φαινόμενο ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ και το φαινόμενο ΣΥΣΣΩΜΑΤΩΣΗ

Το φαινόμενο ΣΥΝΘΕΤΗ ΤΑΛΑΝΤΩΣΗ και το φαινόμενο ΣΥΜΒΟΛΗ ΚΥΜΑΤΩΝ

Το φαινόμενο ΔΙΑΔΟΣΗ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΟΥ ΚΥΜΑΤΟΣ

και το φαινόμενο ΕΞΑΝΑΓΚΑΣΜΕΝΗ ΗΛΕΚΤΡΙΚΗ ΤΑΛΑΝΤΩΣΗ

Το φαινόμενο ΔΙΑΔΟΣΗ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΟΥ ΚΥΜΑΤΟΣ και το φαινόμενο ΔΙΑΘΛΑΣΗ

Τα φαινόμενα «ΚΙΝΗΣΗ ενός rigid body» και «ΕΥΘΥΓΡΑΜΜΗ ΚΙΝΗΣΗ ενός γεωμετρικού σημείου»

Το φαινόμενο ΣΤΡΟΦΙΚΗ ΚΙΝΗΣΗ και το φαινόμενο ΣΥΣΣΩΜΑΤΩΣΗ

Σε κάθε περίπτωση υφίσταται μία τουλάχιστον έννοια η οποία είναι κοινή στην περιγραφή και την ερμηνεία των δύο φαινομένων.

Το φαινόμενο ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ και το φαινόμενο DOPPLER

Σε ένα πρόβλημα που οικοδομείται πάνω στον συνδυασμό

των φαινομένων ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ και DOPPLER, η « κοινή έννοια» είναι η ΤΑΧΥΤΗΤΑ.

Βέβαια το μονοπάτι για τη λύση κάποιου σχετικού προβλήματος μπορεί να εμφανισθεί «αλγεβρικώς δύσβατο» δεδομένου ότι – στο σχολικό βιβλίο - στο φαινόμενο ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ η έννοια ΤΑΧΥΤΗΤΑ εμφανίζεται με την ΑΛΓΕΒΡΙΚΗ ΤΙΜΗ της ενώ στο φαινόμενο DOPPLER η ίδια έννοια - με το ίδιο σύμβολο, υ - εμφανίζεται με το ΜΕΤΡΟ της

Ας δούμε ένα τέτοιο πρόβλημα

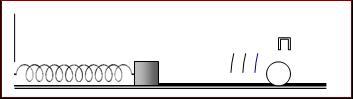
Υποθέτουμε ότι το αντικείμενο που παριστάνεται στο σχήμα - προσδεδεμένο στο άκρο ιδανικού ελατηρίου - συνιστά ανιχνευτή ήχου και ότι μία πηγή Π ηχητικών κυμάτων συχνότητας f βρίσκεται ακίνητη στο συγκεκριμένο σύστημα αναφοράς . Το αντικείμενο ενεργοποιείται έτσι ώστε να εκτελεί οριζόντια κίνηση στο τραπέζι. Σας ζητούμε να προσδιορίσετε το μήκος κύματος του ήχου που εκπέμπει η πηγή Π και η μάζα του αντικειμένου.

Δίδονται η μέγιστη συχνότητα f_max που αντιλαμβάνεται ο αισθητήρας- ανιχνευτής , η ελάχιστη συχνότητα f_min ,που αντιλαμβάνεται ο αισθητήρας- ανιχνευτής το μέγιστο μήκος L_max του ελατηρίου κατά τη διάρκεια της ταλάντωσης, το μικρότερο μήκος L_min του ελατηρίου κατά τη διάρκεια της ταλάντωσης , η ταχύτητα διάδοσης του ήχου και η σταθερά του ελατηρίου. Η τριβή θεωρείται αμελητέα.

Το φαινόμενο ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ κέντρου μάζας και το φαινόμενο ΚΥΛΙΣΗ

Σε ένα πρόβλημα που οικοδομείται πάνω στον συνδυασμό

των φαινομένων ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ κέντρου μάζας και ΚΥΛΙΣΗ, η « κοινή έννοια» θα μπορούσε να είναι η ΕΠΙΤΑΧΥΝΣΗ.

Ας δούμε ένα τέτοιο πρόβλημα

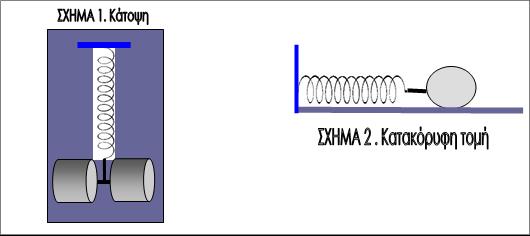
Δύο όμοιοι κύλινδροι συνδέονται με μικρό οριζόντια ραβδί αμελητέας μάζας η ευθεία του οποίου ανήκει σε άξονα συμμετρίας, όπως φαίνεται στο σχήμα 1 σε κάτοψη. Το σύστημα τοποθετείται σε οριζόντιο έδαφος και συνδέεται με ιδανικό ελατήριο αμελητέας μάζας και σταθεράς 200 N/m όπως φαίνεται στο σχήμα 2 . Το ένα άκρο του ελατηρίου είναι ακινητοποιημένο σε κατακόρυφο τοίχο και το άλλο άκρο συνδέεται με το κέντρο μάζας του συστήματος. Το έδαφος δεν είναι λείο έτσι ώστε το σύστημα των δύο κυλίνδρων ενεργοποιούμενο κατάλληλα να

κυλίεται χωρίς ολίσθηση. Η ροπή αδράνειας του συστήματος ως προς τον άξονα στον οποίο ανήκει το μικρό ραβδί να θεωρηθεί ίση με ½mR² , όπου R η ακτίνα και m η μάζα του συστήματος η οποία είναι ίση με 2 kg.

Σας ζητούμε α. να αποδείξετε ότι το ΚΕΝΤΡΟ ΜΑΖΑΣ του συστήματος θα εκτελεί ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ.

β. Να υπολογίσετε την ενέργεια που χρειάστηκε να του μεταβιβάσουμε ώστε το πλάτος της αρμονικής ταλάντωσης να είναι 10 cm.

γ. Με δεδομένη την τιμή του συντελεστή στατικής τριβής μ = 0,4 να υπολογίσετε τη μέγιστη επιμήκυνση του ελατηρίου ώστε η το σύστημα να εκτελεί κύλιση χωρίς ολίσθηση .

Συμβουλή. Για να αποδείξουμε ότι το κέντρο μάζας εκτελεί ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ θα θυμηθούμε ότι το κέντρο μάζας είναι ένα γεωμετρικό σημείο με επιτάχυνση και θα χρειαστεί να αποδείξουμε ότι η τιμή της επιτάχυνσης είναι ανάλογη προς την απομάκρυνση και η κατεύθυνση της είναι διαρκώς προς τη θέση ισορροπίας

Θεωρώντας «σώμα» το μάζας m σύστημα Θα χρειαστεί ακόμα να εφαρμόσουμε σε αυτό τους νόμους του φαινομένου ΚΥΛΙΣΗ (χωρίς ολίσθηση) και συγκεκριμένα τον Δεύτερο νόμο του Νεύτωνα για τη μεταφορική και για τη στροφική κίνηση και τη Διατήρηση της Ενέργειας

Οι ασκούμενες στο σώμα δυνάμεις σε τυχαία στιγμή της κύλισης χωρίς ολίσθηση είναι ( εκτός από τις βάρος και κάθετη αντίδραση) η δύναμη του ελατηρίου και η στατική τριβή. Κατά την εξέλιξη του φαινομένου καμία από τις δύο αυτές δυνάμεις δεν έχει σταθερή τιμή. Η τιμή της στατικής τριβής οφείλει να είναι μικρότερη ή ίση από το γινόμενο μmg.

Τα φαινόμενα «ΚΙΝΗΣΗ ενός ΜΗΧΑΝΙΚΟΥ ΣΤΕΡΕΟΥ »

και «ΕΥΘΥΓΡΑΜΜΗ ΚΙΝΗΣΗ ενός γεωμετρικού σημείου»

Σε ένα πρόβλημα που οικοδομείται πάνω στον συνδυασμό

των φαινομένων αυτών, η « κοινή έννοια» θα μπορούσε να είναι η ΤΑΧΥΤΗΤΑ του κέντρου μάζας

Ας μη μας διαφεύγει ότι η συνήθης «σύνθετη» ενός μηχανικού στερεού είναι ΚΥΛΙΣΗ αλλά θα μπορούσε να είναι και μια άλλη διαφορετική «σύνθετη» κίνηση ΠΟΥ ΔΕΝ ΕΙΝΑΙ ΚΥΛΙΣΗ. Σε κάθε περίπτωση η οποιοδήποτε ΚΙΝΗΣΗ αναλύεται σε ΜΕΤΑΦΟΡΙΚΗ με την ταχύτητα του κέντρου μάζας και σε στροφική περί άξονα που διέρχεται από το κέντρο μάζας

Ας δούμε ένα τέτοιο πρόβλημα

Η μπίλια αφήνεται από

το σημείο Α του κεκλιμένου

επιπέδου, κυλίεται μέχρι

τη βάση του και στη συνέχεια

κυλίεται στον σφαιρικό αγωγό

σχήματος τεταρτοκυκλίου,

διαγράφει τόξο 90⁰ μοιρών

και στη συνέχεια κινείται έτσι

ώστε το κέντρο μάζας της να

εκτελεί κατακόρυφη κίνηση προς τα πάνω.

Με δεδομένα το ύψος h του σημείου Α , την ακτίνα R του τεταρτοκυκλίου, την τιμή g της βαρυτικής επιτάχυνσης

α. Να υπολογίσετε την ταχύτητα του κέντρου μάζας τη στιγμή που φθάνει στο υψηλότερο σημείο Γ του τεταρτοκυκλίου

β. να προσδιορίσετε την κίνηση που θα ακολουθήσει κατά την ανοδική κατακόρυφη κίνηση

γ. Να υπολογίσετε το μέγιστο ύψος στο οποίο θα φθάσει. Η ροπή αδράνειας Ι_cm κάθε σφαίρας είναι ίση με 2mr²/5 .

Συμβουλή. Θεωρούμε σώμα τη μπίλια. Η κίνησή της τόσο στο κεκλιμένο επίπεδο όσο και στον σφαιρικό αγωγό θα είναι ΚΥΛΙΣΗ χωρίς ολίσθηση. Ο ΝΟΜΟΣ τον οποίο θα εφαρμόσουμε είναι η Διατήρηση της Ενέργειας.

Στην επόμενη φάση το γεωμετρικό σημείο «κέντρο μάζας της σφαίρας» θα εκτελεί ΕΥΘΥΓΡΑΜΜΗ ΚΑΤΑΚΟΡΥΦΗ ΚΙΝΗΣΗ την κίνηση δηλαδή την οποία θα εκτελούσε ένα υλικό σημείο με κατακόρυφη προς τα άνω ταχύτητα στο πεδίο βαρύτητας.

Η κίνηση του σώματος μπίλια στη φάση εκείνη χρειάζεται ΠΡΟΣΟΧΗ. Δεν είναι βέβαια πλέον ΚΥΛΙΣΗ αλλά ούτε και μεταφορική κίνηση. Είναι μία σύνθετη κίνηση αναλυόμενη σε μεταφορική με τη συνεχώς μειούμενη ταχύτητα του κέντρου μάζας και σε στροφική με γωνιακή ταχύτητα ΣΤΑΘΕΡΗ περί άξονα που περνά από το κέντρο μάζας. Θα έχει δηλαδή, σε όλη αυτή της φάση, - λόγω της στροφικής κίνησης - τη γωνιακή ταχύτητα που είχε στο σημείο Γ. Τη στιγμή δηλαδή που θα φθάσει στο υψηλότερο σημείο της τροχιάς το κέντρο μάζας θα έχει μηδενική ταχύτητα αλλά η μπίλια ΘΑ ΕΧΕΙ ΚΙΝΗΤΙΚΗ ΕΝΕΡΓΕΙΑ λόγω περιστροφής . Μπορούμε να εφαρμόσουμε και σε αυτή τη φάση τον ΝΟΜΟ Διατήρηση της Ενέργειας παίρνοντας υπόψη ότι η κινητική ενέργεια λόγω στροφικής κίνησης διατηρείται σταθερή

mgh = mgR + ½mυ_cmΓ + ½Ι_cmω² = mgH + ½Ι_cmω²

Ας δούμε ένα ακόμη τέτοιο πρόβλημα

Το μολύβι μήκους L ισορροπεί κατακόρυφο στο άκρο του δακτύλου μας. Το αφήνουμε και εκείνο ( με ασήμαντη αρχική 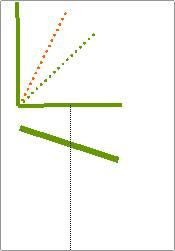ταχύτητα του κέντρου μάζας ) ανατρέπεται, φθάνει σε οριζόντια θέση κατά τη χρονική στιγμή t₁ και στη συνέχεια κινείται προς το πάτωμα. Να υπολογίσετε a. τη γωνιακή ταχύτητα του μολυβιού τη στιγμή που γίνεται οριζόντιο β. το χρονικό διάστημα από τη χρονική στιγμή t₁ που «εγκαταλείπει» το χέρι μας μέχρι τη στιγμή που το κέντρο μάζας του μολυβιού θα έχει κατέλθει κατά h. Το μολύβι να θεωρηθεί ομογενής ράβδος με ροπή αδράνειας ως άξονα που περνά από το άκρο του mL²/3 . Δίνονται τα g, L, h .

Συμβουλή. Θεωρούμε σώμα το μολύβι. Η κίνησή στην πρώτη φάση θα είναι ΣΤΡΟΦΙΚΗ περί άξονα που περνά από το ένα άκρο του. Ο ΝΟΜΟΣ τον οποίο θα εφαρμόσουμε είναι η Διατήρηση της Ενέργειας.

Στην επόμενη φάση το γεωμετρικό σημείο «κέντρο μάζας του μολυβιού » θα εκτελεί ΕΥΘΥΓΡΑΜΜΗ ΚΑΤΑΚΟΡΥΦΗ ΚΙΝΗΣΗ την κίνηση δηλαδή την οποία θα εκτελούσε ένα υλικό σημείο με κατακόρυφη προς τα κάτω ταχύτητα στο πεδίο βαρύτητας. Αν θελήσουμε να περιγράψουμε τη «σύνθετη» κίνηση που εκτελεί το σώμα μολύβι αυτή θα αναλύεται σε μεταφορική με την αυξανόμενη ταχύτητα του κέντρου μάζας και σε στροφική με σταθερή γωνιακή ταχύτητα.

Το φαινόμενο ΔΙΑΔΟΣΗ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΟΥ ΚΥΜΑΤΟΣ

και το φαινόμενο ΔΙΑΘΛΑΣΗ

Σε ένα πρόβλημα που οικοδομείται πάνω στον συνδυασμό

των φαινομένων αυτών, η « κοινή έννοια» θα μπορούσε να είναι η ΤΑΧΥΤΗΤΑ διάδοσης του κύματος

Ας δούμε ένα τέτοιο πρόβλημα

Ένα ηλεκτρομαγνητικό κύμα, αναφερόμενο σε ορισμένη ακτινοβολία διαδιδόμενη σε γυαλί, περιγράφεται με τις εξισώσεις Ε = 20ημ2π(ft –10⁷x/6) και Β = 10^-7ημ2π(ft – 10⁷x/6)

Εάν είναι γνωστό ότι στο γυαλί η μέγιστη τιμή της έντασης του ηλεκτρικού πεδίου είναι ελαττωμένη κατά 20% σε σχέση με εκείνη του κενού. α. Να υπολογίσετε τη συχνότητα του κύματος β. Να καταγράψετε τις αντίστοιχες εξισώσεις κατά τη διάδοσή του στο κενό γ. Να υπολογίσετε τη γωνία διάθλασης εάν η ακτινοβολία προερχόμενη

από το κενό προσπέσει στο γυαλί υπό γωνία 30⁰. Δίνεται c₀ = 3.10⁸m/s

Συμβουλή. Κατά το φαινόμενο ΔΙΑΔΟΣΗ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΟΥ ΚΥΜΑΤΟΣ η έννοια ΤΑΧΥΤΗΤΑ ΔΙΑΔΟΣΗΣ συμμετέχει στον συσχετισμό των τιμών ΕΝΤΑΣΗΣ ΗΛΕΚΤΡΙΚΟΥ ΠΕΔΙΟΥ και ΕΝΤΑΣΗΣ ΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ Ε = Βc καθώς και στη θεμελιώδη εξίσωση των κυμάτων c = λf

Κατά το φαινόμενο ΔΙΑΘΛΑΣΗ κύματος ΔΟΣΗ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΟΥ ΚΥΜΑΤΟΣ η έννοια ΤΑΧΥΤΗΤΑ ΔΙΑΔΟΣΗΣ συμμετέχει στη σχέση για τον δείκτη διάθλασης και τη σχέση μεταξύ των τιμή της ΓΩΝΙΑΣ ΠΡΟΣΠΤΩΣΗΣ με τη ΓΩΝΙΑ ΔΙΑΘΛΑΣΗΣ c₀/c = ημθ₁/ ημθ₂