2007.

Απολυτήριες Εξετάσεις

Γ΄ τάξης

στη ΦΥΣΙΚΗ Κατεύθυνσης

Το πρώτο θέμα

1. Η εξίσωση του φορτίου του πυκνωτή σε ένα κύκλωμα ηλεκτρικών ταλαντώσεων LC, το οποίο εκτελεί αμείωτες ηλεκτρικές ταλαντώσεις μέγιστου φορτίου Q και γωνιακής συχνότητας ω, δίνεται από τη σχέση q = Qσυνωt .

Η εξίσωση της έντασης του ρεύματος στο κύκλωμα δίνεται από τη σχέση

α. i = - Qωημωt β . i = - Q/ω.ημωt

γ. i = Qωσυνωt δ. i = Qωημωt ( Μονάδες 5 )

2. Κατά την φθίνουσα μηχανική ταλάντωση

α. το πλάτος διατηρείται σταθερό β. η μηχανική ενέργεια διατηρείται

γ. το πλάτος μεταβάλλεται σύμφωνα με τη σχέση Α = Α₀ e ^Λt

δ . έχουμε μεταφορά ενέργειας από το ταλαντούμενο σύστημα στο περιβάλλον

( Μονάδες 5 )

3. Σε ένα ηλεκτρομαγνητικό κύμα το ηλεκτρικό και το μαγνητικό πεδίο

α. έχουν διαφορά φάσης ίση με x/λ β. έχουν λόγο Β/Ε = c

γ. έχουν διανύσματα που είναι κάθετα στη διεύθυνση διάδοσης

δ. δεν υπακούουν στην αρχή της επαλληλίας ( Μονάδες 5 )

4. Σε μία ελαστική κρούση δεν διατηρείται

α. η κινητική ενέργεια του συστήματος

β. η ορμή του συστήματος

γ. η μηχανική ενέργεια του συστήματος

δ. η κινητική ενέργεια κάθε σώματος ( Μονάδες 5 )

5. Να γράψετε στο τετράδιό σας το γράμμα κάθε πρότασης και δίπλα σε κάθε γράμμα τη λέξη Σωστό, για τη σωστή πρόταση και τη λέξη Λάθος, για τη λανθασμένη

α. Κατά τη διάδοση ενός κύματος μεταφέρεται ενέργεια από ένα σημείο σε ένα άλλο, αλλά δεν μεταφέρεται ούτε ύλη ούτε ορμή. Λάθος

β. Το ορατό φως είναι μέρος της ηλεκτρομαγνητικής ακτινοβολίας, την οποία ανιχνεύει το ανθρώπινο μάτι. Σωστό

γ. Σε στάσιμο κύμα, μεταξύ δύο διαδοχικών δεσμών, όλα τα σημεία έχουν την ίδια φάση Σωστό

δ. Η ροπή αδράνειας ενός σώματος σταθερής μάζας έχει πάντα την ίδια τιμή Λάθος

ε. Η περίοδος και η συχνότητα ενός περιοδικού φαινομένου είναι μεγέθη αντίστροφα Σωστό ( Μονάδες 5 )

Το δεύτερο θέμα

Για τις παρακάτω ερωτήσεις να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.

1. Μεταξύ δύο ακίνητων παρατηρητών Β και Α κινείται πηγή S με σταθερή ταχύτητα υ_s πλησιάζοντας προς τον Α. Οι παρατηρητές και η πηγή βρίσκονται στην ίδια ευθεία. Η πηγή εκπέμπει ήχο μήκους κύματος λ, ενώ οι παρατηρητές Α και Β αντιλαμβάνονται μήκος κύματος λ₁ και λ₂ αντίστοιχα. Τότε για το μήκος κύματος του εκπέμπει η πηγή θα ισχύει:

α . λ = (λ₁+λ₂ )/2 β. λ = (λ₁- λ₂ )/2 γ. λ = λ₁λ₂ / (λ₁+λ₂ ) ( Μονάδες 2 )

Να αιτιολογήσετε την απάντησή σας. ( Μονάδες 6 )

2. Ένα αυτοκίνητο Α μάζας Μ βρίσκεται σταματημένο σε κόκκινο φανάρι. Ένα άλλο αυτοκίνητο Β μάζας m , ο οδηγός του οποίου είναι απρόσεκτος, πέφτει στο πίσω μέρος του αυτοκινήτου Α. Η κρούση θεωρείται κεντρική και πλαστική. Αν αμέσως μετά την κρούση το συσσωμάτωμα έχει το 1/3 της κινητικής ενέργειας αμέσως πριν την κρούση, τότε θα ισχύει:

α. m/M = 1/6 β. m/M = 1/2 α. m/M = 1/3 ( Μονάδες 2 )

Να αιτιολογήσετε την απάντησή σας. ( Μονάδες 7 )

3. Κολυμβητής βρίσκεται κάτω από την επιφάνεια της θάλασσας και παρατηρεί τον ήλιο . Η θέση που τον βλέπει είναι

α. πιο ψηλά από την πραγματική του θέση.

β. ίδια με την πραγματική του θέση

γ. πιο χαμηλά από την πραγματική του θέση ( Μονάδες 2 )

Να αιτιολογήσετε την απάντησή σας. ( Μονάδες 6 )

Το τρίτο θέμα

Σε μία χορδή δημιουργείται στάσιμο κύμα, η εξίσωση του οποίου είναι y = 10συν πx/4 ημ20πt

Όπου x και y δίνονται σε cm και t σε s. Να βρείτε

α. το μέγιστο πλάτος της ταλάντωσης, τη συχνότητα και το μήκος κύματος ( Μονάδες 6 )

β. τις εξισώσεις των δύο κυμάτων που παράγουν το στάσιμο κύμα ( Μονάδες 6 )

γ. την ταχύτητα που έχει τη χρονική στιγμή t= 0 ένα σημείο της χορδής το οποίο απέχει από το άκρο της x = 3cm ( Μονάδες 6 )

δ. σε ποιες θέσεις υπάρχουν κοιλίες μεταξύ των σημείων x_Α = 3 cm και x_B = 9 cm ( Μονάδες 7 )

Δίνονται π = 3,14 και συν3π/4 = - √2/2

Το τέταρτο θέμα

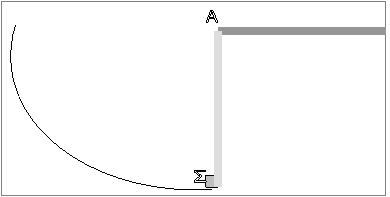
Ομογενής ράβδος μήκους L = 0,3 m και μάζας Μ = 1,2 kg μπορεί να περιστρέφεται χωρίς τριβές γύρω από οριζόντιο άξονα που διέρχεται από το άκρο της Α. Αρχικά την κρατούμε σε οριζόντια θέση και στη συνέχεια την αφήνουμε ελεύθερη. Θεωρούμε την αντίσταση του αέρα αμελητέα.

α. Να βρείτε τη γωνιακή επιτάχυνση της ράβδου ως προς τον άξονα περιστροφής τη στιγμή που αφήνεται ελεύθερη ( Μονάδες 5 )

β. Να βρείτε τη στροφορμή της ράβδου όταν φθάσει σε κατακόρυφη θέση. ( Μονάδες 5 )

Τη στιγμή που η ράβδος φθάνει στην κατακόρυφη θέση το κάτω άκρο της ράβδου συγκρούεται ακαριαία με ακίνητο σώμα Σ αμελητέων διαστάσεων που έχει μάζα m = 0,4 kg. Μετά την κρούση το σώμα κινείται κατά μήκος κυκλικού τόξου ακτίνας L, ενώ η ράβδος συνεχίζει να κινείται κατά την ίδια φορά. Δίνεται ότι η γωνιακή ταχύτητα της ράβδου αμέσως μετά την κρούση είναι ω/5, όπου ω η γωνιακή ταχύτητά της αμέσως πριν την κρούση.

γ. Να βρείτε την ταχύτητα του σώματος Σ αμέσως μετά την κρούση ( Μονάδες 7 ) δ. Να βρείτε το ποσοστό της μηχανικής ενέργειας που μετατράπηκε σε θερμική ενέργεια κατά την κρούση ( Μονάδες 8 )

Δίνονται : η ροπή αδράνειας της ράβδου ως προς τον άξονα Α, Ι = 1/3 ΜL² και g = 10 m/s².

Δίνονται : η ροπή αδράνειας της ράβδου ως προς τον άξονα Α, Ι = 1/3 ΜL² και g = 10 m/s².

Ανδρέας Ιωάννου Κασσέτας

Οι λύσεις και τα σχόλια

Το πρώτο θέμα

1. Αν συμφωνήσουμε στο «ποια θα θεωρήσουμε αρχή των χρόνων» και η συνάρτηση φορτίου χρόνου είναι η q = Qσυνωt η συνάρτηση i = f(t) θα είναι η

i = - Qωημωt

2. Κατά την φθίνουσα μηχανική ταλάντωση

α. το πλάτος δεν διατηρείται σταθερό , η μηχανική ενέργεια ελαττώνεται το

γ. σε περίπτωση που η αντιτιθέμενη δύναμη είναι της μορφής F = -bυ το πλάτος μεταβάλλεται σύμφωνα με τη σχέση Α = Α₀ e^-Λt με όχι σύμφωνα με τη σχέση Α = Α₀ e^Λt

δ . έχουμε μεταφορά ενέργειας από το ταλαντούμενο σύστημα στο περιβάλλον

3. Σε ένα ηλεκτρομαγνητικό κύμα το ηλεκτρικό και το μαγνητικό πεδίο

δεν έχουν διαφορά φάσης ίση με x/λ Οι τιμές των εντάσεων έχουν πηλίκο E/B ίσο με την ταχύτητα του ηλεκτρομαγνητικού κύματος

γ. περιγράφονται με διανύσματα κάθετα στη διεύθυνση διάδοσης

δ. υπακούουν στην αρχή της επαλληλίας

4. Κατά την εξέλιξη του φαινομένου «ελαστική κρούση» α. διατηρείται η κινητική ενέργεια του συστήματος διότι με βάση αυτή τη διατήρηση ορίζεται η « ελαστική κρούση» β. διατηρείται η ορμή του συστήματος εφόσον υπονοείται ότι κατά την εξέλιξη του φαινομένου δεν ασκούνται εξωτερικές δυνάμεις

γ. η επιλογή της έννοιας «μηχανική ενέργεια του συστήματος» πρέπει να θεωρηθεί ατυχής.

δ. το ότι μεταβάλλεται «η κινητική ενέργεια κάθε σώματος» το οποίο θεωρείται ΣΩΣΤΗ απάντηση - από την Κεντρική επιτροπή - στην ειδική περίπτωση που τα σώματα έχουν ίσες μάζες και αντίθετες ταχύτητες ΔΕΝ ΙΣΧΥΕΙ.

Προτεινόμενη ΑΝΑΔΙΑΤΥΠΩΣΗ για την επόμενη φορά

4. Σε μία ελαστική κρούση δύο σωμάτων με διαφορετικές μάζες δεν διατηρείται

α. η κινητική ενέργεια του συστήματος

β. η ορμή του συστήματος

γ. η μάζα του συστήματος

δ. η κινητική ενέργεια κάθε σώματος

5. α. Κατά τη διάδοση ενός κύματος μεταφέρεται ενέργεια από ένα σημείο σε ένα άλλο, αλλά δεν μεταφέρεται ούτε ύλη ούτε ορμή.

Είναι ΛΑΘΟΣ . Κατά τη διάδοση ενός κύματος μεταφέρεται ενέργεια και ορμή

β. Το ορατό φως είναι μέρος της ηλεκτρομαγνητικής ακτινοβολίας, την οποία

ανιχνεύει το ανθρώπινο μάτι. Η πρόταση της Επιτροπής είναι να θεωρηθεί ΣΩΣΤΟ.

Ωστόσο, σύμφωνα και με την εύστοχη παρατήρηση που μου έστειλε με email o συνάδελφος από το Ελληνικό Διονύσης Μητρόπουλος, εάν διαβαστεί με έμφαση στη λέξη «ΜΕΡΟΣ» ότι δηλαδή

« Το ορατό φως είναι ένα μέρος (μόνο) της ηλεκτρομαγνητικής ακτινοβολίας,

την οποία ανιχνεύει το ανθρώπινο μάτι » υποδηλώνει ότι το μάτι μας είναι σε θέση να ανιχνεύει και ακτινοβολίες έξω από την περιοχή του ορατού φωτός.

Σε αυτή την περίπτωση , δυστυχώς για την Κεντρική Επιτροπή,

η απάντηση του οξυδερκούς μαθητή θα είναι «λάθος».

γ. Σε στάσιμο κύμα, μεταξύ δύο διαδοχικών δεσμών, όλα τα σημεία έχουν την ίδια φάση . Αν και ο όρος «φάση ενός σημείου» είναι αδόκιμος, η διατύπωση αυτή υποδηλώνει κάτι που είναι ΣΩΣΤΟ.

δ. Η ροπή αδράνειας ενός σώματος σταθερής μάζας έχει πάντα την ίδια τιμή

Η ροπή αδράνειας αναφέρεται σε σώμα και σε άξονα. Η διατύπωση έχει ασάφεια. Στη σκέψη ενός μαθητή που έχει εμβαθύνει στις έννοιες δημιουργεί ποικίλα «ίσως» Ίσως υποδηλώνει την «ως προς ορισμένο άξονα ροπή αδράνειας» η οποία μπορεί να μεταβληθεί αν συμβεί αναδιάταξη των τμημάτων του σώματος χωρίς μεταβολή μάζας, όπως η χορεύτρια στον πάγο. Ίσως πάλι υποδηλώνει ότι ένα rigid body έχει διαφορετική ροπή αδράνειας ως προς κάθε άξονα.

Πάντως με δεδομένη και την ασάφεια η απάντηση είναι ότι είναι ΛΑΘΟΣ.

ε. Η περίοδος και η συχνότητα ενός περιοδικού φαινομένου είναι μεγέθη αντίστροφα Είναι ΣΩΣΤΟ.

Το δεύτερο θέμα

1. Μεταξύ δύο ακίνητων παρατηρητών Β και Α κινείται πηγή S με σταθερή ταχύτητα υ_s πλησιάζοντας προς τον Α. Οι παρατηρητές και η πηγή βρίσκονται στην ίδια ευθεία. Η πηγή εκπέμπει ήχο μήκους κύματος λ, ενώ οι παρατηρητές Α και Β αντιλαμβάνονται μήκος κύματος λ₁ και λ₂ αντίστοιχα. Τότε για το μήκος κύματος του εκπέμπει η πηγή θα ισχύει:

α . λ = (λ₁+λ₂ )/2 β. λ = (λ₁- λ₂ )/2 γ. λ = λ₁λ₂ / (λ₁+λ₂ )

η ΑΠΑΝΤΗΣΗ

Πρόκειται για ΦΑΙΝΟΜΕΝΟ Doppler

Ο παρατηρητής Α αντιλαμβάνεται ήχο συχνότητας f₁ = f u_ηχ/(υ_ηχ - υ_s)

Ο παρατηρητής B αντιλαμβάνεται ήχο συχνότητας f₂ = f u_ηχ/(υ_ηχ + υ_s)

Για το μήκος κύματος λ₁ ισχύει υ_ηχ = λ₁f₁

Για το μήκος κύματος λ₂ ισχύει υ_ηχ = λ₂f₂

Για το μήκος κύματος λ ισχύει υ_ηχ = λf

Από τις σχέσεις αυτές απορρέει ότι λ = (λ₁+λ₂ )/2

Μια άλλη προσέγγιση. Το μήκος κύματος που αντιλαμβάνεται ο ακροατής όταν πλησιάζει προς αυτόν η πηγή του ήχου είναι λ₁ = λ - υ_s Τ

Το μήκος κύματος που αντιλαμβάνεται ο ακροατής όταν η πηγή του ήχου απομακρύνεται από αυτόν είναι λ₂ = λ + υ_sΤ .

Από τις δύο αυτές σχέσεις απορρέει ότι λ₁+λ₂ = 2λ άρα λ = (λ₁+λ₂ )/2

2. Ένα αυτοκίνητο Α μάζας Μ βρίσκεται σταματημένο σε κόκκινο φανάρι. Ένα άλλο αυτοκίνητο Β μάζας m , ο οδηγός του οποίου είναι απρόσεκτος, πέφτει στο πίσω μέρος του αυτοκινήτου Α. Η κρούση θεωρείται κεντρική και πλαστική. Αν αμέσως μετά την κρούση το συσσωμάτωμα έχει το 1/3 της κινητικής ενέργειας αμέσως πριν την κρούση, ( εννοεί της κινητικής ενέργειας που είχε το αυτοκίνητο Α πριν την κρούση ) τότε θα ισχύει:

α. m/M = 1/6 β. m/M = 1/2 α. m/M = 1/3

η ΑΠΑΝΤΗΣΗ

Κατά τη διάρκεια της συσσωμάτωσης δεν ασκούνται εξωτερικές δυνάμεις άρα διατηρείται η ορμή του συστήματος Αν είναι υ η ταχύτητα του αυτοκινήτου Α και V η ταχύτητα του συσσωματώματος εφαρμόζουμε τον νόμο Διατήρηση της ορμής στο σύστημα . mυ = ( m + M)V

Το δεδομένο ότι «το συσσωμάτωμα έχει το 1/3 της κινητικής ενέργειας που είχε το αυτοκίνητο Α πριν από την κρούση», αξιοποιείται με τη σχέση ½(m +M)V² = ½ mυ²/3

Από τις δύο σχέσεις προκύπτει ότι m/M = ½

3. Κολυμβητής βρίσκεται κάτω από την επιφάνεια της θάλασσας και παρατηρεί τον ήλιο . Η θέση που τον βλέπει είναι α. πιο ψηλά από την πραγματική του θέση. β. ίδια με την πραγματική του θέση γ. πιο χαμηλά από την πραγματική του θέση

Παρατήρηση

Οι επιλογές « ήλιος» και « σχήμα με τον ήλιο λοξά » δεν είναι ιδιαίτερα επιτυχείς. Τίθεται καταρχάς το ερώτημα «πόσο ψηλά φαίνεται ο ήλιος, όταν είμαστε έξω από το νερό ; » ώστε να έχει νόημα το ΨΗΛΟΤΕΡΑ. Για να συνδεθεί το ζήτημα με την εμπειρία, η «φαινομένη ανύψωση» το αντικείμενο έπρεπε να μην είναι ο ήλιος αλλά ένα οποιοδήποτε «επίγειο» αντικείμενο το οποίο να βρίσκεται σε ορισμένη απόσταση από το έδαφος αλλά και – για να δημιουργηθεί σημειακό είδωλο από τη διάθλαση - να βρίσκεται στην ίδια κατακόρυφο με τον κολυμβητή

η ΑΠΑΝΤΗΣΗ

Τον ήλιο τον βλέπει πιο ψηλά λόγω της διάθλασης του ηλιακού φωτός από τον αέρα στο νερό. Το νερό, σε σχέση με τον αέρα είναι οπτικώς πυκνότερο. Η ταχύτητα του φωτός σε αυτό είναι μικρότερη , ο δείκτης διάθλασης είναι μεγαλύτερος. Με βάση τον σχετικό νόμο κάθε φωτεινή ακτίνα προερχόμενη από τον αέρα διαθλώμενη στην επιφάνεια του νερού πλησιάζει στην κάθετο, δημιουργείται με άλλα λόγια γωνία διάθλασης μικρότερη από τη γωνία πρόσπτωσης. Με ένα σχήμα μπορεί να δειχθεί ότι κάθε λεπτή δέσμη που φθάνει στο μάτι του κολυμβητή μετά τη διάθλαση των ακτίνων φαίνεται να προέρχεται από κάποιο σημείο ψηλότερα από εκείνο που βρίσκεται η φωτεινή πηγή.

Το τρίτο θέμα

Σε μία χορδή δημιουργείται στάσιμο κύμα, η εξίσωση του οποίου είναι y = 10συνπx/4.ημ20πt

Όπου x και y δίνονται σε cm και t σε s. Να βρείτε

α. το μέγιστο πλάτος της ταλάντωσης, τη συχνότητα και το μήκος κύματος

β. τις εξισώσεις των δύο κυμάτων που παράγουν το στάσιμο κύμα γ. την ταχύτητα που έχει τη χρονική στιγμή t= 0,1 s ένα σημείο της χορδής το οποίο απέχει από το άκρο της x = 3cm

δ. σε ποιες θέσεις υπάρχουν κοιλίες μεταξύ των σημείων x_Α = 3 cm και x_B = 9 cm

Δίνονται π = 3,14 και συν3π/4 = - √2/2

Η ΦΥΣΙΚΗ

Φανταζόμαστε δύο αρμονικά κύματα του ίδιου πλάτους και της ίδιας συχνότητας να διαδίδονται στο ίδιο ελαστικό μέσο προς αντίθετες κατευθύνσεις και να συμβάλλουν. Επιδιώκουμε να προβλέψουμε θεωρητικά το αποτέλεσμα της συμβολής.

Για να το πετύχουμε απλοποιούμε το μοντέλο μας θεωρώντας ότι τα δύο κύματα είναι εγκάρσια και ότι οι ταλαντώσεις γίνονται στο ίδιο επίπεδο.

Επιλέγουμε έναν άξονα x΄x με κριτήριο να συμπίπτει με τη διεύθυνση της διάδοσης. Ως αρχή των αξόνων επιλέγουμε ένα γεωμετρικό σημείο το οποίο θα συμπίπτει βέβαια με τη θέση ισορροπίας κάποιου σημειακού ταλαντωτή, ας τον ονομάσουμε Ο.

Για λόγους απλούστευσης η επιλογή της αρχής των αξόνων γίνεται με το εξής κριτήριο.

«Αν η κίνηση που θα εκτελούσε ο ταλαντωτής Ο λόγω του προς τα δεξιά κύματος περιγράφεται με την εξίσωση

y = Aημωt, η κίνηση που θα εκτελούσε, ο ίδιος ταλαντωτής, λόγω του προς τα αριστερά διαδιδόμενου κύματος να περιγράφεται με την y΄= Aημωt »

Αυτό σημαίνει ότι η αρχή των αξόνων επιλέγεται έτσι ώστε η σύνθετη κίνηση του ταλαντωτή Ο που έχει ως θέση ισορροπίας το σημείο αυτό να περιγράφεται με την εξίσωση y = 2Aημωt, η ότι «ο ταλαντωτής που βρίσκεται στην αρχή των αξόνων να εκτελεί αρμονική ταλάντωση με πλάτος 2 Α».

Θεωρούμε τώρα έναν άλλο (σημειακό) ταλαντωτή , τον Μ, με θέση ισορροπίας κάποιο γεωμετρικό σημείο του θετικού ημιάξονα σε απόσταση + x, από την αρχή των αξόνων.

Λόγω του προς τα δεξιά διαδιδόμενου κύματος η κίνηση του Μ περιγράφεται με την

y_Μ1 = Aημω(t- x/c). Ας δούμε και πώς επηρεάζεται ο Μ λόγω του προς τα αριστερά διαδιδόμενου κύματος. Το κύμα αυτό δημιουργεί, όπως είπαμε, στον Ο την ταλάντωση y΄ = Aημωt. Λόγω αυτού του προς τα αριστερά κύματος ο ταλαντωτής Ο θα πρέπει σε κάθε στιγμή ΝΑ ΕΧΕΙ την απομάκρυνση την οποία ΕΙΧΕ ο Μ πριν από χρόνο x/c.

Αυτό σημαίνει ότι εφόσον η εξίσωση κίνησης του Ο λόγω του προς τα αριστερά κύματος είναι η y ΄ = Aημωt

η εξίσωση κίνησης του Μ λόγω του ίδιου αυτού κύματος θα είναι η y_Μ2 = Aημω(t+ x/c).

Ο ταλαντωτής Μ συμμετέχει όμως και στις δύο κινήσεις με συνέπεια η εξίσωση της κίνησής του να είναι

y = Aημω (t- x/c) + Aημω(t+ x/c) άρα y = 2Aσυν(ωx/c) ημωt ή y = 2Aσυν(2πx/λ) ημ(2πx/Τ)

Για τον συγκεκριμένο ταλαντωτή Μ, τη σχέση αυτή τη «βλέπουμε» ως μία ημιτονοειδή συνάρτηση της απομάκρυνσης y με τον χρόνο t και μπορούμε να συμπεράνουμε ότι « η κίνηση είναι αρμονική ταλάντωση πλάτους 2Aσυν(2πx/λ).

Η σχέση y = 2Aσυν(2πx/λ) ημ(2πx/Τ) επιβεβαιώνει την ύπαρξη δεσμών και κοιλιών και - με βάση την επιλογή που κάναμε- στην αρχή των αξόνων βρίσκεται μία κοιλία.

Το σύμβολο x συνεπώς παριστάνει την απόσταση από μία κοιλία.

ΟΙ ΛΥΣΕΙΣ

να βρείτε

α. το μέγιστο πλάτος της ταλάντωσης, τη συχνότητα και το μήκος κύματος

Η δική μας πρόταση για μία ΑΝΑΔΙΑΤΥΠΩΣΗ

α . την τιμή του μέγιστου από τα πλάτη των ταλαντώσεων των υλικών σημείων της χορδής

τη συχνότητα των ταλαντώσεων και

το μήκος κύματος καθενός από τα δύο κύματα που δημιουργούν το στάσιμο

η ΛΥΣΗ

Από τον συσχετισμό της γενικής y = 2Aσυν(2πx/λ) ημ(2πx/Τ) με τη δεδομένη

y = 10συνπx/4.ημ20πt προκύπτει ότι το μέγιστο των πλατών είναι ίσο με 10 cm ,

η συχνότητα των ταλαντώσεων 10 Hz και το μήκος κύματος καθενός από τα δύο κύματα που δημιουργούν το στάσιμο λ = 8 cm .

β. τις εξισώσεις των δύο κυμάτων που παράγουν το στάσιμο κύμα

η ΛΥΣΗ

Αν η εξίσωση για το ένα κύμα είναι η y = Aημ2π (t/Τ- x/λ)

για το άλλο θα είναι η y =Aημ2π(t/Τ + x/λ)

Αντικαθιστώντας y = 5ημ2π (10t- x/8) y = 5ημ2π (10t+x/8) ( t σε s , x σε cm )

Οι εξισώσεις είναι έτσι δομημένες ώστε το x να παριστάνει την απόσταση από τη θέση ισορροπίας μιας κοιλίας

γ. την ταχύτητα που έχει τη χρονική στιγμή t= 0,1 s ένα σημείο της χορδής

το οποίο απέχει από το άκρο της x = 3cm

Το σχόλιο: Η Κεντρική Επιτροπή αγνοεί άραγε ότι το x παριστάνει την απόσταση από τη θέση ισορροπίας μιας κοιλίας και ότι το άκρο μιας χορδής δεν είναι υποχρεωτικά μια κοιλία; Βέβαια, με καθυστέρηση μιας ώρας ήρθε η «ΔΙΟΡΘΩΣΗ» που έλεγε

«απέχει 3 cm από το σημείο x = 0».

Επαναδιατύπωση

Την ταχύτητα που έχει τη χρονική στιγμή t = 0,1 s ένα υλικό σημείο της χορδής, η θέση ισορροπίας του οποίου είναι η x = + 3cm

η ΛΥΣΗ

Το σημείο με x = + 3cm εκτελεί αρμονική ταλάντωση η οποία με βάση την αρχική συμφωνία για αρχή των χρόνων περιγράφεται με την y = 10συνπ.3/4.ημ20πt

άρα y = - 5 √2 ημ20πt . Η αλγεβρική τιμή της ταχύτητάς του θα περιγράφεται συνεπώς με την υ = - 5 √2 . 20π. συν20πt υ = -√2 100π συν20πt.

Για t = 0,1 s η ( αλγεβρική) τιμή της ταχύτητάς του θα είναι υ = -√2 100π cm/s

δ. σε ποιες θέσεις υπάρχουν κοιλίες μεταξύ των σημείων

x_Α = 3 cm και x_B = 9 cm.

η ΛΥΣΗ

Στην αρχή των αξόνων βρίσκεται η θέση ισορροπίας μιας κοιλίας. Η αμέσως επόμενη - εφόσον το μήκος κύματος είναι 8cm - θα βρίσκεται σε απόσταση λ/2 = 4cm από την αρχή των αξόνων και η μετά από αυτήν σε 8 cm από την αρχή των αξόνων. Και οι δύο αυτές κοιλίες – και μόνον αυτές - βρίσκονται μεταξύ των σημείων x_Α = 3cm και x_B = 9cm

Αν θέλουμε μια λύση πιο «φορμαλιστική» μπορούμε να πούμε ότι σε x = κλ/2 βρίσκονται κοιλίες και να αναζητήσουμε τους ακέραιους κ για τους οποίους 9cm > κ.λ/2> 3cm ή 9cm > κ. 4cm > 3cm ή 9/4 > κ > 3/4

Το τέταρτο θέμα

α. Να βρείτε τη γωνιακή επιτάχυνση της ράβδου ως προς τον άξονα περιστροφής τη στιγμή που αφήνεται ελεύθερη

Η ΛΥΣΗ . Τη χρονική εκείνη στιγμή σημειώνουμε τις ασκούμενες στη ράβδο δυνάμεις. Είναι η δύναμη βάρος και η δύναμη από τον άξονα. Εφαρμόζουμε τον δεύτερο νευτωνικό νόμο για τη στροφική κίνηση. τ = Ι_Α α_γων Αγνοούμε τον «μύθο» ( σχολικό βιβλίο σελ. 112) ότι « θεωρούμε θετική τη ροπή της δύναμης που τείνει να στρέψει το σώμα ΑΝΤΙΘΕΤΑ από τη φορά των δεικτών του ρολογιού » και θεωρούμε θετική τη ροπή κάθε δύναμης που τείνει να στρέψει τη ράβδο κατά τη φορά των δεικτών του ρολογιού προσανατολισμού. Από τις ασκούμενες δυνάμεις μόνο η βάρος έχει ροπή ως προς Α. τ = ΜgL/2. Δίνεται ότι Ι_Α = 1/3 ΜL² α_γων = 3g/ 2L α_γων = 50rad/s²

β. Να βρείτε τη στροφορμή της ράβδου όταν φθάσει σε κατακόρυφη θέση.

ΑΝΑΔΙΑΤΥΠΩΣΗ

β. Να βρείτε την - ως προς το σημείο Α - στροφορμή της ράβδου

όταν φθάσει σε κατακόρυφη θέση

Η ΛΥΣΗ . Η ζητούμενη στροφορμή ως προς Α είναι ίση με το γινόμενο « ροπή αδράνειας Ι_Α επί γωνιακή ταχύτητα ω » . Για να υπολογίσουμε τη γωνιακή ταχύτητα ω εφαρμόζουμε τον νόμο «Διατήρηση της ενέργειας» κατά την κίνηση της ράβδου από την οριζόντια θέση μηδενικής γωνιακής ταχύτητας στην κατακόρυφη θέση. Θεωρούμε επίπεδο αναφοράς για τη δυναμική ενέργεια το οριζόντιο επίπεδο που περνάει από το χαμηλότερο σημείο Σ της ράβδου . Σε κάθε περίπτωση η ( βαρυτική) δυναμική ενέργεια της ράβδου είναι ίση με το γινόμενο Mgh_cm όπου h_cmη απόσταση του κέντρου μάζας από το οριζόντιο επίπεδο αναφοράς.

0 + MgL = ½ I_Aaω² + ΜgL/2

Δεδομένου ότι Ι_Α = 1/3 ΜL² αν θα είναι τελικά στην ω² = 3g/L άρα το μέτρο της γωνιακής ταχύτητας θα είναι ω = 10rad/s. Η τιμή της ζητούμενης στροφορμής θα είναι συνεπώς

Ι_Α ω = 1/3 ΜL² ω = 36.10^-2Js

Παρατήρηση

Με το ερώτημα β αξιολογείται ο διδασκόμενος

α. στο εάν γνωρίζει με τι είναι ίση η στροφορμή ενός στρεφομένου στερεού

β. εάν μπορεί να επινοήσει ότι ο απαιτούμενος νόμος για την εύρεση της γωνιακής ταχύτητας είναι η Διατήρηση ενέργειας ( ή και το θεώρημα έργου ενέργειας )

γ. εάν γνωρίζει με τι είναι ίση η κινητική ενέργεια στρεφομένου στερεού

δ. εάν γνωρίζει με τι είναι ίση η δυναμική ενέργεια σώματος με διαστάσεις.

Οι ΠΕΝΤΕ μόνο μονάδες για όλα αυτά είναι δυσανάλογα λίγες δεδομένου ότι στο ερώτημα δ για την % μεταβολή της κινητικής ενέργειας δίδονται ΟΚΤΩ μονάδες

γ. Να βρείτε την ταχύτητα του σώματος Σ αμέσως μετά την κρούση

Η ΛΥΣΗ . Κατά την εξέλιξη του φαινομένου κρούση δεν η ως προς το σημείο Α εξωτερική ροπή στο ΣΥΣΤΗΜΑ «ράβδος – σώμα Σ» είναι μηδενική. Άρα η - ως προς Α - ΣΤΡΟΦΟΡΜΗ ΤΟΥ ΣΥΣΤΗΜΑΤΟΣ «ράβδος – σώμα Σ» ΔΙΑΤΗΡΕΙΤΑΙ. Εφαρμόζουμε τον νόμο Διατήρηση της στροφορμής στο συγκεκριμένο σύστημα. Εξισώνουμε την ως προς Α στροφορμή πριν από την κρούση ( που είναι η στροφορμή Ι_Α ω = 36.10^-2Js) με την ως προς Α στροφορμή μετά την κρούση. Η μετά την κρούση στροφορμή είναι το διανυσματικό άθροισμα « στροφορμή της ράβδου και στροφορμή του Σ» . Η στροφορμή της ράβδου μετά την κρούση θα είναι – βάσει του δεδομένου - Ι_Α ω/5 ενώ η ως προς το σημείο Α στροφορμή του Σ είναι mυL δεδομένου ότι το Σ θεωρείται υλικό σημείο .Εφόσον και τα τρία αντίστοιχα διανύσματα έχουν την ίδια κατεύθυνση

Ι_Α ω = Ι_Α ω/5 + muL υ = 2,4 m/s

δ. Να βρείτε το ποσοστό της μηχανικής ενέργειας που μετατράπηκε

σε θερμική ενέργεια κατά την κρούση

Παρατήρηση

Μηχανική ενέργεια – όρος αρκετά ξεπερασμένος και πρέπει να τον εγκαταλείψουμε – θεωρείται το άθροισμα κινητικής και δυναμικής ενέργειας. Μπορεί η μεταβολή βαρυτικής δυναμικής ενέργειας να είναι ανεξάρτητη από το «ποιο οριζόντιο επίπεδο αναφοράς θα επιλέξουμε» αλλά το ποσοστό μεταβολής δεν είναι ανεξάρτητο από το οριζόντιο επίπεδο αναφοράς. Συνεπώς κάθε ερώτηση για «ποσοστό μεταβολής ΜΗΧΑΝΙΚΗΣ ΕΝΕΡΓΕΙΑΣ» στερείται νοήματος . Βέβαια με μια ώρα καθυστέρηση η διατύπωση διορθώθηκε σε «Να βρείτε το ποσοστό της κινητικής που μετατράπηκε σε θερμική ενέργεια κατά την κρούση»

Και μάλιστα με τη διατύπωση αυτή η Κεντρική Επιτροπή Γενικών Εξετάσεων, χρησιμοποιώντας την έννοια «θερμική ενέργεια», απέφυγε το περίφημο «θερμότητα» το οποίο επιμένει να χρησιμοποιεί το σχολικό βιβλίο παρά τις επανειλημμένες παρατηρήσεις μας πάνω στο ζήτημα.

Η ΛΥΣΗ . Η κινητική ενέργεια του συστήματος πριν από την κρούση ήταν Κ_πριν = ½ Ι_Α ω² .

Η κινητική ενέργεια του συστήματος μετά την κρούση ήταν Κ_μετά = ½Ι_Αω₁² +½ mυ², όπου ω₁ = ω/5 Κατά την κρούση δηλαδή η κινητική ενέργεια μειώθηκε κατά ½Ι_Αω₁² +½mυ² - ½Ι_Α ω²

Το % ποσοστό της μείωσης θα είναι Κ_πριν - Κ_μετά / Κ_πριν . 100 = 32.

θα είναι δηλαδή 32 %

ΑΞΙΟΛΟΓΗΣΗ των θεμάτων

Σε σχέση με τα αντίστοιχα των τριών παρελθόντων ετών τα θέματα θεωρούμε ότι είναι λίγο πιο εύκολα για το σύνολο των μαθητών .

Η εκτίμηση βέβαια αυτή δεν μπορεί να αποδειχθεί παρά μόνο μετά τη βαθμολόγηση των γραπτών . Παρά τις σοβαρές αντιρρήσεις μας για ορισμένες από τις διατυπώσεις η συνολική μας εκτίμηση είναι ότι καθώς κυλούν τα χρόνια βελτιώνεται η ποιότητα των διατυπώσεων αλλά και η σαφήνεια των ζητουμένων.