Ανδρέας Ιωάννου Κασσέτας

Η αεροσυνοδός και ο κτηνοτρόφος

Το αεροσκάφος με τον πρωθυπουργό πετάει προς τη Θεσσαλονίκη. Ο Μακεδόνας κτηνοτρόφος σηκώνει το κεφάλι και το αναγνωρίζει. Με το βλέμμα της σκέψης παρακολουθεί τον πρωθυπουργό να απομακρύνεται από αυτόν με μεγάλη ταχύτητα.

Ο εαυτός του είναι το κέντρο του Σύμπαντος, η έδρα της σκέψης του, το σύστημα αναφοράς, η αρχή των αξόνων. Είναι λοιπόν σίγουρος πως τη στιγμή εκείνη ο πρωθυπουργός μετακινείται.

« Καθισμένος στη θέση του ο πρωθυπουργός παραμένει ακίνητος» σκέφτεται την ίδια στιγμή η ιπταμένη αεροσυνοδός καθώς τον παρακολουθεί μέσα εννοείται στο σκάφος. Τον βλέπει με τα μάτια της σκεπτικό και απόλυτα ήρεμο να μη μετακινείται.

Το ίδιο αντικείμενο την ίδια χρονική στιγμή κινείται αλλά και δεν κινείται .

« Ας λέει ότι θέλει η συνοδός εγώ ξέρω ότι ο πρωθυπουργός πηγαίνει στη Θεσσαλονίκη» είναι έτοιμος να ορκιστεί ο Μακεδόνας αγρότης.

« Και όμως δεν κινείται ο πρωθυπουργός» θα επιμείνει εκείνη. «Εσύ απομακρύνεσαι από αυτόν» θα μπορούσε να του πει αν είχαν επικοινωνία. « Όσο για τη Θεσσαλονίκη, αυτή σε λίγο θα φανεί καθώς, κινούμενη διαρκώς έρχεται προς το αεροπλάνο».

Η Αλεξάνδρεια που φεύγει

Κι αποχαιρέτα την

Την Αλεξάνδρεια που φεύγει

Κωνσταντίνος Καβάφης

Τελικά ποιος φεύγει; Ο Αντώνιος ή η Αλεξάνδρεια ; Ή μήπως πρέπει να αγνοήσουμε τη διάζευξη και να δεχθούμε πως η Πόλη φεύγει από τον Αντώνιο και ο Αντώνιος από την Πόλη; Οι φυσικοί πάντως υποστηρίζουν ότι και οι δύο οπτικές είναι εννοιακά ισοδύναμες. Η «Αλεξάνδρεια που φεύγει «είναι η γλώσσα της ποίησης. Διαποτισμένη από την ελευθερία της σκέψης αναστατώνει την τρέχουσα λογική αλλά υιοθετείται από τη Φυσική και συνιστά εξαιρετικό παράδειγμα για να φωτίσει κανείς την ισοδυναμία των Συστημάτων Αναφοράς, το θεμέλιο της Σχετικότητας .

η ΚΙΝΗΣΗ είναι ΣΧΕΤΙΚΗ όπως και η ΑΛΗΘΕΙΑ.

Αλλάζει μόλις αλλάξει το Σύστημα Αναφοράς

MPEG Encoded Sequence (Reference - seriously degraded by compression).

Εξίσωση κίνησης του Πειραιά

Το καραβάκι έχει σαλπάρει από το λιμάνι του Πειραιά για τη Σαλαμίνα κι ένα σωρό οι καθηγητές που πάνε απέναντι να διδάξουν στο Λύκειο Αμπελακίων με διευθυντή τον Λάμπρο Ασημακόπουλο. Ανάμεσά τους μία ευφάνταστη πι έψιλον τέσσερα, βλέπει τον Πειραιά να απομακρύνεται και σκέφτεται να φτιάξει εξισώσεις κίνησης. Θεωρεί μια δική της αρχή των χρόνων επτά και τέσσερα πρώτα λεπτά και ο Πειραιάς περιγράφεται ως κινούμενο αντικείμενο με εξισώσεις θέσης . Στην αποβάθρα ένας λιμενεργάτης κοιτάζει προς το μέρος της πόλης και φυσικά είναι σίγουρος ότι ο Πειραιάς μένει στη θέση του. Θα μπορούσε να βάλει και στοίχημα .

Το λαμπάκι στο ποδήλατο.

Ένα πορτοκαλί λαμπάκι είναι στερεωμένο στη ζάντα του ποδήλατου. Για τον ποδηλάτη η τροχιά του είναι κυκλική αλλά για έναν παρατηρητή στο έδαφος η τροχιά του ίδιου αντικειμένου είναι κυκλοειδής. Όσο για το φανάρι του ποδήλατου ο ποδηλάτης βλέπει να βρίσκεται σε σταθερή απόσταση και εκτιμά ότι είναι ακίνητο. Για τον Άλλο όμως παρατηρητή το ίδιο φανάρι εμφανίζει τροχιά ευθύγραμμη.

Η κίνηση μετά από οριζόντια βολή αναλύεται σε . . .

Λέει στους μαθητές του πως η κίνηση μιας - θεωρούμενης υλικό σημείο - πέτρας, μετά την οριζόντια εκτόξευσή της αναλύεται

σε οριζόντια ευθύγραμμη ομαλή και

σε ελεύθερη πτώση

αλλά εκείνοι καθισμένοι στα θρανία το μόνο που μπορούν να διακρίνουν - με το βλέμμα της σκέψης - είναι την παραβολική τροχιά

αναζητεί λοιπόν μία διδακτική προσέγγιση τέτοια που να τους βοηθήσει να διακρίνουν τις δύο αυτές κινήσεις

Θα μπορούσε να προτείνει σε καθένα από αυτούς να φανταστεί την κίνηση ως παρατηρητής κινούμενος μεταφορικά με σταθερή οριζόντια ταχύτητα την ταχύτητα εκτόξευσης

οπότε θα μπορούσε ίσως να φανταστεί την πέτρα να πέφτει ελεύθερα

Η κύλιση αναλύεται σε . . .

Λέει στους μαθητές του ότι η κύλιση ενός τροχού αναλύεται

σε ΜΕΤΑΦΟΡΙΚΗ κίνηση με την ταχύτητα του κέντρου μάζας και

σε ΣΤΡΟΦΙΚΗ περί άξονα που περνά από το κέντρο μάζας

και αναζητεί μία διδακτική προσέγγιση τέτοια που να τους βοηθήσει να διακρίνουν τις δύο αυτές κινήσεις

Το καλύτερο που έχει να κάνει είναι να προτείνει σε καθένα από αυτούς να φανταστεί την κίνηση ως παρατηρητής με κιάλια σε «μικρό ελικόπτερο» που κινείται μεταφορικά με την ταχύτητα του κέντρου μάζας. Όπως κατεβαίνει ο τροχός από ένα κεκλιμένο επίπεδο κατεβαίνει και το ελικόπτερο παράλληλα. Καθώς θα βλέπει με τα κιάλια τον τροχό θα μπορέσει ίσως με τη φαντασία του να διακρίνει ότι εκτελεί μόνο στροφική κίνηση.

Το οικοδόμημα που πολύ αργότερα ονομάστηκε Φυσική χτίστηκε πάνω στο φαινόμενο ΚΙΝΗΣΗ.

Αυτά που κινούνται είναι αντικείμενα και τα αντικείμενα βρίσκονται στον χώρο.

Για να μπορέσει η Φυσική να προσδιορίσει τη θέση τους με μαθηματικές δομές,

αξιοποιώντας τη γεωμετρική κληρονομιά, τα αγγίζει με το μαγικό της ραβδί

και τα μετατρέπει σε ΥΛΙΚΑ ΣΗΜΕΙΑ

Κάνοντας την επιλογή αυτή η Φυσική άφησε να διεισδύσει στο εσωτερικό της

η Γεωμετρία και στη συνέχεια η Ανάλυση. Είναι ο τρόπος με τον οποίο οικοδομήθηκε.

Η έννοια ΣΗΜΕΙΟ – point, punkt, point, punto , punto , ponto , точки –

ανήκει στη ΓΕΩΜΕΤΡΙΑ. Το βασικό στοιχείο ταυτότητας είναι η ΘΕΣΗ του.

Από τη στιγμή που παρεμβαίνουν οι φυσικοί, εισάγουν

την έννοια χρόνος και διαπιστώνουν η θέση του σημείου αλλάζει αποδίδουν

στο σημείο μία μετατόπιση, ένα ρυθμό στη μεταβολή της θέσης, την ταχύτητα

και ένα ρυθμό μεταβολής της ταχύτητας, την επιτάχυνση . Εξυπακούεται ότι

ένα γεωμετρικό σημείο – όπως λόγου χάρη το κέντρο μάζας – «δεν έχει»

ορμή, κινητική ενέργεια, στροφορμή ούτε και νοείται η δράση μιας δύναμης σε αυτό.

Το ΥΛΙΚΟ ΣΗΜΕΙΟ - particle, point materiel, massepunkt , punto materiale , punto material, ponto material материальная точка - είναι έννοια της ΦΥΣΙΚΗΣ.

Υποδηλώνει αντικείμενο με αδράνεια του οποίου τις διαστάσεις μπορούμε να αγνοήσουμε έτσι που κάθε χρονική στιγμή να «κατοικεί» σε ένα γεωμετρικό σημείο – η θέση του δηλαδή είναι η θέση του γεωμετρικού αυτού σημείου – και εκτός από ταχύτητα και επιτάχυνση μπορεί να έχει ορμή, κινητική ενέργεια , στροφορμή καθώς και να δρα κάποια δύναμη πάνω του.

Η έννοια ΣΥΣΤΗΜΑ ΣΥΝΤΕΤΑΓΜΕΝΩΝ ανήκει στα ΜΑΘΗΜΑΤΙΚΑ .

Συνδέεται με μια εξαιρετική απάντηση των μαθηματικών στο ερώτημα

« ΠΟΥ βρίσκεται ένα γεωμετρικό σημείο ; » .

Ιδιαίτερα γόνιμη αποδείχθηκε η ιδέα του Καρτέσιου . Το 1637 στο « Περί μεθόδου Λόγος»

Discours de la Methode στο τρίτο από τα παραδείγματα που πρότεινε με τίτλο

«Η Γεωμετρία » προώθησε την ιδέα ότι ένα ζεύγος αριθμών μπορεί να προσδιορίσει

τη θέση ενός γεωμετρικού σημείου σε μία επιφάνεια.

Το ΚΑΡΤΕΣΙΑΝΟ ΣΥΣΤΗΜΑ ΣΥΝΤΕΤΑΓΜΕΝΩΝ που δημιουργήθηκε μπορεί

- εκτός των άλλων -

να εικονοποιήσει μία ΑΛΓΕΒΡΙΚΗ δομή και να την παρουσιάσει

ως ΓΕΩΜΕΤΡΙΚΗ ΑΝΑΠΑΡΑΣΤΑΣΗ , τη λεγόμενη ΓΡΑΦΙΚΗ ΠΑΡΑΣΤΑΣΗ

cartesian Coordinate system kartesisches Koordinatensystem

système de coordonnées cartésien sistema coordinato cartesiano

sistema coordinado cartesiano sistema coordenado cartesian

Дескартес Координировать систему ديكارت تنسيق نظام

In mathematics, the Cartesian coordinate system is used to determine each point uniquely in a plane through two numbers, usually called the x-coordinate and the y-coordinate of the point. Using the Cartesian coordinate system geometric shapes (such as curves) can be described by algebraic equations

Dans les mathématiques, le système de coordonnées cartésien est employé pour déterminer chaque point uniquement dans un planpar deux nombres, habituellement appelés x-coordonner et y-coordonner du point. Employer les formes géométriques cartésiennes de système du même rang (telles que des courbes) peut être décrit par des équations algébriques

In der Mathematik wird das kartesische beigeordnete System benutzt, um jeden Punkt in einer Plan durch zwei Zahlen einzigartig festzustellen, normalerweise genannt x-koordinieren und vom Punkt y-koordinieren. Das Verwenden der kartesischen beigeordnetes System geometrischen Formen (wie Kurven) kann durch algebraische Gleichungen beschrieben werden

Στη περίπτωση ευκλείδειου χώρου τριών διαστάσεων το ΚΑΡΤΕΣΙΑΝΟ ΣΥΣΤΗΜΑ ΣΥΝΤΕΤΑΓΜΕΝΩΝ συγκροτείται από τρεις άξονες x, y, z καθένας από τους οποίους είναι «εφοδιασμένος» με ένα μοναδιαίο διάνυσμα.

Ο βασικός πρωταγωνιστής είναι η λεγόμενη ΑΡΧΗ ΤΩΝ ΑΞΟΝΩΝ, το γεωμετρικό δηλαδή σημείο στο οποίο τέμνονται οι άξονες

Η έννοια ΣΥΣΤΗΜΑ ΑΝΑΦΟΡΑΣ ανήκει στη ΦΥΣΙΚΗ. Παραπέμπει σε συγκεκριμένο παρατηρητή με ανθρώπινη συνείδηση ο οποίος παρακολουθεί, περιγράφει, ερμηνεύει και προβλέπει. Χωρίς αυτήν το φαινόμενο ΚΙΝΗΣΗ

και οι έννοιες μετατόπιση, ταχύτητα, επιτάχυνση, γωνιακή ταχύτητα,

γωνιακή επιτάχυνση, δύναμη, ροπή, κινητική ενέργεια, ορμή,

στροφορμή - ακόμα και στην κλασική Φυσική - δεν έχουν

σημασιακό περιεχόμενο.

Για τους φυσικούς η ΚΙΝΗΣΗ είναι ΣΧΕΤΙΚΗ.

Ως σύστημα αναφοράς συνήθως - οχι πάντα - χρησιμοποιήσουν

ένα ΚΑΡΤΕΣΙΑΝΟ ΣΥΣΤΗΜΑ ΣΥΝΤΕΤΑΓΜΕΝΩΝ

που το φαντάζονται να προσδένεται σε κάποιο σώμα ενώ συγχρόνως

φαντάζονται τον παρατηρητή να συμπίπτει με την Αρχή των αξόνων

Frame of reference Bezugsrahmen Référenciel Frame di riferimento

Frame de la referencia Frame da referência Oриентиров الاطار المرجعي

Αν έχουμε ένα σύνολο από συστήματα συντεταγμένων μεταξύ τους ακίνητα, η ΘΕΣΗ ενός σημειακού αντικειμένου μπορεί να είναι για καθένα από αυτά διαφορετική αλλά – εφόσον με το κύλημα του χρόνου το σημειακό αντικείμενο αλλάζει θέση – η ΜΕΤΑΤΟΠΙΣΗ του είναι ίδια για όλα αυτά τα συστήματα. Το σύνολο των συστημάτων αυτών συνιστά ένα «χωρικό» ΣΥΣΤΗΜΑ ΑΝΑΦΟΡΑΣ με το οποίο οι φυσικοί μπορούν να περιγράψουν την κίνηση.

Χρησιμοποιούν δύο τύπους Συστημάτων Αναφοράς. Το ΑΔΡΑΝΕΙΑΚΟ και το ΜΗ ΑΔΡΑΝΕΙΑΚΟ.

A Frame of reference is a certain perspective, by which the universe is observed. Specifically in physics, he refers to a provided set of axes, from which an observer can measure the position and the movement of all points in a system, as well as the determining position of the articles in him. There are two kinds’ reference frameworks: Inertia and non-inertia.

Ein Bezugsrahmen ist eine bestimmte Perspektive, von der das Universum beobachtet wird. Spezifisch in der Physik, bezieht sich er auf einen zur Verfügung gestellten Satz äxte, von denen ein Beobachter die Position und die Bewegung aller Punkte in einem System messen kann, sowie die Lagebestimmung der Gegenstände in ihm. Es gibt zwei Arten Bezugsrahmen: Trägheits- und nicht-Trägheits.

Le référenciel est une perspective particulière dont on observe l'univers. Spécifiquement, dans la physique, elle se rapporte à un ensemble fourni de haches à partir desquelles un observateur peut mesurer la position et le mouvement de tous les points dans un système, aussi bien que l'orientation des objets dans elle. Il y a deux types des reférenciels : à inertie et non-à inertie.

Un frame di riferimento è una prospettiva particolare da cui l'universo è osservato. Specificamente, nella fisica, si riferisce ad un insieme fornito delle ascie da cui un osservatore può misurare la posizione ed il movimento di tutti i punti in un sistema, così come l'orientamento degli oggetti in esso. Ci sono due tipi di telai di riferimento: inerziale e non-inerziale.

Un frame de la referencia es una perspectiva particular de la cual se observa el universo. Específicamente, en la física, refiere a un sistema proporcionado de las hachas de las cuales un observador puede medir la posición y el movimiento de todos los puntos en un sistema, así como la orientación de objetos en él. Hay dos tipos de frames de la referencia: de inercia y no-de inercia.

Κατά τη διδασκαλία του φαινομένου « ευθύγραμμη κίνηση» διαπιστώνεται ότι

δεν είναι λίγοι οι μαθητές που συγχέουν τις έννοιες

ΚΑΡΤΕΣΙΑΝΟ ΣΥΣΤΗΜΑ ΣΥΝΤΕΤΑΓΜΕΝΩΝ και ΣΥΣΤΗΜΑ ΑΝΑΦΟΡΑΣ

Τι συμπεραίνετε από το παρακάτω γράφημα μιας ευθύγραμμης κίνησης ;

Η ερώτηση τέθηκε σε μαθητές της Γ΄ Γυμνασίου

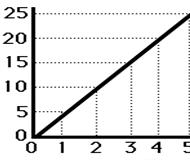
Ένα ποσοστό περίπου 30 % των μαθητών απάντησε

« διαπιστώνω ότι η ΚΙΝΗΣΗ ΕΙΝΑΙ ΕΥΘΥΓΡΑΜΜΗ »

Ένα σύστημα αναφοράς λέγεται ΑΔΡΑΝΕΙΑΚΟ

εφόσον σε αυτό ισχύει

ο πρώτος νευτωνικός νόμος της κίνησης, ο νόμος της αδράνειας

Κάθε σύστημα αναφοράς που κινείται με σταθερή ταχύτητα

ως προς ένα αδρανειακό σύστημα αναφοράς είναι κι αυτό αδρανειακό

O δάσκαλός μας ο Γαλιλαίος μας δίδαξε να φέρνουμε στο μυαλό μας δύο ερευνητές,

ο ένας σε σύστημα αναφοράς Σ, ο άλλος σε σύστημα αναφοράς Σ’,

κινούμενο μεταφορικά ως προς το Σ με σταθερή ταχύτητα u

και να ασχολούνται με το ίδιο σωματίδιο

ένα σωματίδιο, το Ρ, και δύο συστήματα αναφοράς το Σ και το Σ΄

Θεωρούμε Αρχή των χρόνων τη στιγμή που τα δύο συστήματα ταυτίζονται

η ΘΕΣΗ

Κινούμενο με ταχύτητα u ως προς το Σ ,

τη χρονική στιγμή t η θέση του σωματιδίου Ρ για τον ερευνητή στο Σ΄ είναι x΄, y΄ , z΄

τη ίδια χρονική στιγμή t η θέση του ίδιου σωματιδίου Ρ για τον ερευνητή στο Σ είναι

x = x΄+ u_xt y = y΄+ u_yt z = z΄+ u_zt

η ΤΑΧΥΤΗΤΑ υ_x = υ_x΄+ u_x υ_y = υ_y΄+ u_y υ_z = υ_z΄+ u_z

η ΕΠΙΤΑΧΥΝΣΗ α_x = α_x΄ α_y = α=΄ α = α_z΄

η ΜΑΖΑ m = m΄

η ΔΥΝΑΜΗ F = F΄

οι δύο αδρανειακοί παρατηρητές ασχολούμενοι με το ίδιο σωματίδιο

διαπιστώνουν διαφορετική ΘΕΣΗ και διαφορετική ΤΑΧΥΤΗΤΑ

αλλά ίδια ΕΠΙΤΑΧΥΝΣΗ και ΜΑΖΑ άρα ίδιες και τις ασκούμενες σε αυτό ΔΥΝΑΜΕΙΣ.

Αυτά σύμφωνα με την κλασική Μηχανική

Κάθε σύστημα αναφοράς που έχει επιτάχυνση ως προς ένα αδρανειακό σύστημα θεωρείται μη αδρανειακό

δύο ερευνητές, ο ένας σε σύστημα αναφοράς Σ,

ο άλλος σε σύστημα αναφοράς Σ’, κινούμενο μεταφορικά ως προς το Σ με επιτάχυνση α_σ

ασχολούνται με το ίδιο σωματίδιο Ρ.

η ΕΠΙΤΑΧΥΝΣΗ

Εάν η επιτάχυνση του Ρ για το Σ, είναι α_Ρ και

η επιτάχυνση του Ρ για το Σ΄, είναι α_Ρ΄

α_Ρ = α_Ρ΄+ α_σ α_Ρ΄= α_Ρ – α_σ ( σχέση διανυσμάτων )

η ΜΑΖΑ

Εάν η μάζα ενός σωματιδίου Ρ για το Σ είναι m και η μάζα του ίδιου σωματιδίου, για το Σ΄ είναι m΄

m = m΄

η ΔΥΝΑΜΗ

Εάν η ολική δύναμη η ασκούμενη σε ένα σωματίδιο για τον παρατηρητή στο Σ είναι F

και η ολική δύναμη η ασκούμενη στο ίδιο σωματίδιο για τον παρατηρητή στο Σ΄ είναι F΄ ισχύει

F΄ = F - ma_σ ( σχέση διανυσμάτων )

Για τον ερευνητή στο Σ΄, η ολική δύναμη στο σωματίδιο είναι, εκτός από την F,

ΚΑΙ ΜΙΑ ΔΥΝΑΜΗ «ΑΔΡΑΝΕΙΑΣ» ίση με -ma_σ

όπου m η μάζα του σωματιδίου και α_σ η επιτάχυνση του συστήματος Σ΄,άρα και του ερευνητή, ως προς το

Για να εφαρμόσουμε τους νόμους της κλασικής Μηχανικής σε μη αδρανειακό συστήματα σε μεταφορική κίνηση

εισάγουμε τη ΔΥΝΑΜΗ ΑΔΡΑΝΕΙΑΣ.

Ποια είναι η κίνηση του δίσκου ;

Ο ομογενής δίσκος βρίσκεται ακίνητος στο έδαφος. Σε κάποια χρονική στιγμή ασκείται δύναμη στο περιφερειακό σημείο Β η οποία στη συνέχεια διατηρείται σταθερή ασκούμενη συνεχώς στο ίδιο υλικό σημείο Β. Το κέντρο μάζας θα εκτελεί ευθύγραμμη κίνηση με σταθερή επιτάχυνση. Ποια θα είναι η κίνηση του δίσκου ;

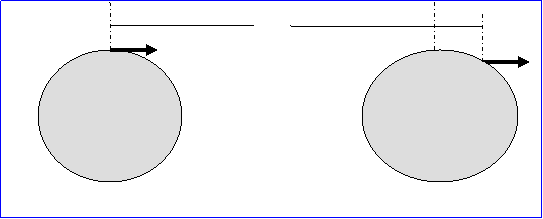
Η Σκέψη μας δεν μπορεί να συνδυάσει τις δύο κινήσεις. Και μια ιδέα είναι «τη μία – προσωρινά – να την ξεφορτωθεί». Έχει εξάλλου επίγνωση ότι η μορφή μιας κίνησης εξαρτάται από το Σύστημα Αναφοράς. Επιλέγει λοιπόν ένα τέτοιο Σύστημα Αναφοράς ώστε τη μία από τις κινήσεις - την πιο φανερή στη μορφή της- να την ξεφορτωθεί.

Γινόμαστε λοιπόν φανταστικοί επιβάτες ενός φανταστικού -μικροσκοπικού σαν κουνούπι- ελικόπτερου το οποίο αρχικά είναι ακίνητο και στη συνέχεια ξεκινάει μαζί με τον δίσκο, πετάει πάνω του με επιτάχυνση ίση με την επιτάχυνση του κέντρου μάζας ΚΑΙ ΠΑΡΑΤΗΡΟΥΜΕ την κίνησή του δίσκου. Τώρα ΕΧΟΥΜΕ ΚΑΤΟΨΗ η οποία μπορεί να οδηγήσει στη διαμόρφωση της ΑΠΟΨΗΣ ΓΙΑ ΤΗΝ ΚΙΝΗΣΗ.

Ως παρατηρητές λοιπόν στο επιταχυνόμενο σύστημα κάνουμε αυτά που μας λέει η Φυσική.

Σημειώνουμε στον δίσκο εκτός από τη δύναμη F ( στο σημείο Β) και μια δύναμη αδρανείας στο κέντρο μάζας του δίσκου . Η δύναμη αδρανείας έχει μέτρο ma ίσο δηλαδή με το γινόμενο « μάζα δίσκου επί επιτάχυνση του συστήματος αναφοράς» με κατεύθυνση αντίθετη από εκείνη της επιτάχυνσης του Συστήματος Αναφοράς.

Έχουμε τώρα μπροστά μας ζεύγος δύο δυνάμεων.

Από αυτές, η μεν δύναμη αδρανείας ασκείται συνεχώς στο κέντρο μάζας ενώ η άλλη είναι βέβαια σταθερή αλλά ΑΣΚΕΙΤΑΙ ΣΤΟ ΣΗΜΕΙΟ Β του στρεφόμενου δίσκου το οποίο αλλάζει συνεχώς θέση με συνέπεια η ΡΟΠΗ του ζεύγους να είναι μεταβαλλόμενη.

Στην αρχή των χρόνων η ροπή του ζεύγους είναι ίση με το γινόμενο FR όπου R η ακτίνα αλλά στη συνέχεια, καθώς το Β κινείται κυκλικά, η ροπή του ζεύγους ελαττώνεται δεδομένου ότι μειώνεται η απόσταση των δύο φορέων. Αυτό, σύμφωνα με τον νόμο για τη στροφική κίνηση, σημαίνει ότι ο αρχικά ακίνητος δίσκος αρχίζει να στρέφεται η γωνιακή του ταχύτητα αυξάνεται αλλά ο ρυθμός αύξησης – η γωνιακή επιτάχυνση- μειώνεται. Σε κάποια στιγμή όταν το Β έχει διαγράψει τόξο 90 μοιρών οι δύο δυνάμεις δεν συνιστούν ζεύγους ή, με άλλα λόγια, η ροπή είναι μηδέν. Τη στιγμή εκείνη ο δίσκος έχει τη μεγαλύτερη γωνιακή ταχύτητα και στη συνέχεια η ροπή του ζεύγους είναι επιβραδυντική. Τη στιγμή που το Β έχει διαγράψει τόξο 180 μοιρών, ο δίσκος σταματάει για να αρχίσει και πάλι να στρέφεται σε αντίθετη φορά και το σημείο Β να διαγράφει τόξο 180 μέχρι να επανέλθει στην αρχική του θέση για να επαναληφθεί το ίδιο. Αξίζει να σημειώσουμε ότι σε κάθε κίνηση του Β κατά 180⁰ το έργο της F είναι συνολικά μηδέν. Ο ΔΙΣΚΟΣ ΕΚΤΕΛΕΙ ΣΤΡΟΦΙΚΗ ΤΑΛΑΝΤΩΣΗ η οποία δεν είναι αρμονική.

Το συμπέρασμα:

Η κίνηση του δίσκου μπορεί να αναλυθεί

σε μεταφορική με την ταχύτητα του κέντρου μάζας και

σε στροφική ταλάντωση.