Ανδρέας Ιωάννου Κασσέτας

Διδασκαλία Φυσικής στην Α΄ Γυμνασίου

Η μέτρηση του μήκους

1. Να μετρήσουμε μια απόσταση 2. Το μέγεθος του πλανήτη Γη

3. Το μήκος και το «ένα μέτρο μήκους» 4. Πόσο είναι «ένα μέτρο μήκους » ; Γιατί είναι «τόσο» και δεν είναι λιγότερο ή περισσότερο;

5. Η πρακτική των φυσικών να χρησιμοποιούν σύμβολα

6. Το μήκος του κύκλου και η ακτίνα του

Υλικό για αξιολόγηση Παραπομπές

Εξυπακούεται ότι, σε σχέση με τα προτεινόμενα, ο καθηγητής του μαθήματος θα μπορούσε να επιλέξει ΚΑΠΟΙΟ Ή ΚΑΠΟΙΑ από αυτά ή και κανένα από αυτά με κριτήριο το « ταιριάζουν ή δεν ταιριάζουν με το ύφος της διδασκαλίας του». Θα μπορούσε επίσης με «έναυσμα» από αυτά να διαμορφώσει μια «δική του» διδασκαλία

1. Να μετρήσουμε μια απόσταση

O διδάσκων καλεί τους μαθητές να συμπληρώσουν το φύλλο εργασίας

Φύλλο εργασίας .

« Πόσο απέχει ; »

1. Ο αριστερός τοίχος της αίθουσας από τον δεξιό

α. Η απάντηση μου με βάση αυτό που βλέπω ........................................

β. Μια καλύτερη προσέγγιση μετά από μέτρηση ........................................

2. Η πόρτα του σχολείου από την πόρτα του σπιτιού μου

α. Η απάντηση μου, σύμφωνα με αυτό που νομίζω ........................................

β. Μια καλύτερη προσέγγιση ........................................

3. Το κέντρο της Αθήνας από το κέντρο της Θεσσαλονίκης

α. Η απάντηση μου, σύμφωνα με ότι φαντάζομαι ή έχω ακούσει ........................................

β. Μια καλύτερη προσέγγιση ........................................

4. Η Αθήνα από το Λος Άντζελες

α. Η απάντηση μου, σύμφωνα με ότι φαντάζομαι ή έχω ακούσει ........................................

β. Μια καλύτερη προσέγγιση ........................................

5. Ο ισημερινός της Γης από τον Βόρειο πόλο

α. Η απάντηση μου, σύμφωνα με ότι με ότι φαντάζομαι ή έχω ακούσει ........................................

β. Μια καλύτερη προσέγγιση ........................................

Οι μαθητές αναζητούν απαντήσεις στο Διαδίκτυο – στο σχολείο είτε στο σπίτι τους - είτε περιορίζονται σε κάποια εκτίμηση.

Και ενώ για την απόσταση Αθήνα Λος Άντζελες, 11.086 χιλιόμετρα περίπου , η ακρίβεια στην απάντηση για την απόσταση Ισημερινός – Βόρειος εντυπωσιάζει .

«10.000 χιλιόμετρα ακριβώς »

Πώς είναι δυνατόν να έχουμε τέτοια ακρίβεια;. Το ερώτημα καταγράφεται χωρίς απάντηση.

Για τη μέτρηση της απόστασης των δύο απέναντι τοίχων, ο διδάσκων αναφέρεται στον Λεονάρντο ντα Βίντσι.

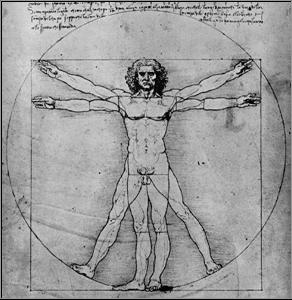Θα μπορούσε λόγου χάρη να πει: «Κάποτε διάβασα κάτι που είχε προσέξει ο Λεονάρντο ντα Βίντσι. Το ύψος κάθε ανθρώπου είναι ίσο με την απόσταση των άκρων του δακτύλων του όταν έχει τεντωμένα τα χέρια του. Αυθόρμητα τέντωσα τα χέρια μου και ήταν αδύνατον να πιστέψω ότι αυτή η απόσταση είναι ίση με το ύψος μου. Μέτρησα προσεκτικά στη συνέχεια την απόσταση των άκρων των χεριών μου και βρήκα ακριβώς 1 μέτρο και 80 εκατοστά , ήταν απολύτως ίση με το ύψος μου». Προβάλλει στη συνέχεια το σχέδιο του Da Vinci με τον Uomo vitruviano.

Θέτει το ερώτημα «ποιοι από τους μαθητές ξέρουν με κάποια ακρίβεια πόσο είναι το ύψος τους . Επιλέγει από αυτούς τρεις μαθητές και τρεις μαθήτριες και ζητεί από καθένα και καθεμία να απαντήσει – εάν το γνωρίζει - στο «πόσο είναι το ύψος του/της» . Ένας άλλος μαθητής καταγράφει το όνομα και το ύψος καθενός από τους έξι στον πίνακα.

Ο διδάσκων στη συνέχεια τους καλεί να επινοήσουν τρόπο για να μετρηθεί η απόσταση των τοίχων εύκολα. Υπάρχει σοβαρό ενδεχόμενο κάποιος να επινοήσει τη μέτρηση με τους μαθητές όρθιους με τεντωμένα χέρια, ο ένας μετά τον άλλο. Επειδή η απόσταση δεν θα είναι ακριβώς τόση προσθέτει ο ίδιος με τις παλάμες του προσθέτοντας ότι η παλάμη του τεντωμένη είναι 24 (λόγου χάρη ) εκατοστά.

Στη συνέχεια ενθαρρύνει μια μέτρηση με «πόδια Γιάννη» για να καταλήξει στο ότι η απόσταση των τοίχων είναι 23 «πόδια Γιάννη» ακριβώς ή «23 πόδια Γιάννη και κάτι».

Πώς μετράμε τις αποστάσεις ;

Από την εποχή των πρώτων μετρήσεων μέχρι σήμερα όλες οι κοινωνικές ομάδες αναζήτησαν

μια «κοινή μονάδα» για να μετρούν αποστάσεις. Μονάδες που σχετίζονταν με το

ανθρώπινο σώμα και την ανθρώπινη κίνηση χρησιμοποιήθηκαν επί αιώνες σχεδόν αποκλειστικά.

Το πόδι, ο βραχίονας, το βήμα έπαιξαν το ρόλο τους με διάφορες παραλλαγές .

Οι Έλληνες χρησιμοποίησαν τον πόδα, το στάδιο, το πλέθρο και τον παρασάγγη, ενώ οι Ρωμαίοι το πόδι και το μίλι, δηλαδή απόσταση που αντιστοιχούσε σε 1000 διπλά βήματα.

Μια πρόταση που θα ξέφευγε από το ανθρώπινο σώμα ήταν εκείνη που έκαναν οι Γάλλοι. Πρότειναν η νέα μονάδα μέτρησης να βασίζεται στο μέγεθος του πλανήτη Γη.

2. Το μέγεθος του πλανήτη Γη.

Τον πλανήτη μας τον φανταζόμαστε τεράστιο και «είναι τεράστιος»,

σε σχέση με το δικό μας μέγεθος.

Δύο περίπου αιώνες πριν από τον Χριστό,

ο Ερατοσθένης¹ επινόησε τρόπο και μέτρησε

την ακτίνα του πλανήτη

Η ακόμα καλύτερη μέτρηση

των Γάλλων στα τέλη του 18ου αιώνα σχεδιάστηκε και έγινε με σκοπό να προταθεί

μια παγκόσμια μονάδα για τη μέτρηση του μήκους με βάση το μέγεθος του πλανήτη Γη.

3. Το μήκος και το «ένα μέτρο μήκους»

Στην ελληνική γλώσσα, η λέξη μήκος αναφέρεται σε ένα αντικείμενο, όπως το μολύβι που γράφουμε και σημαίνει την απόσταση δύο σημείων του. Το μήκος ενός φερμουάρ είναι η βασική πληροφορία για το μέγεθός του. Όταν όμως ένας σπουργίτης ανοίξει τα φτερά του, το μέγεθός του περιγράφεται όχι μόνο από το άνοιγμά τους, αλλά και από την απόσταση ράμφους-ουράς . Εκτός από το μήκος, η γλώσσα μας χρησιμοποιεί και άλλες λέξεις όπως το πάχος, το πλάτος και το ύψος. Καθεμιά από αυτές υπονοεί την απόσταση ανάμεσα σε δύο σημεία. Την απόσταση δύο σημείων τη μετράμε με υποδεκάμετρο, με διαστημόμετρο, με μετροταινία. Ως μονάδα μέτρησης η Φυσική χρησιμοποιεί το ένα μέτρο. Γράφουμε «1m»

4. Πόσο είναι «ένα μέτρο μήκους » ; Γιατί είναι «τόσο» και δεν είναι λιγότερο ή περισσότερο;

Την περίοδο της Γαλλικής Επανάστασης ξεκίνησε μια προσπάθεια για την καθιέρωση μονάδων μέτρησης που θα ίσχυαν για όλους τους λαούς και σε όλες τις εποχές

Το 1791 η Γαλλική Εθνοσυνέλευση όρισε μια επιτροπή από επιστήμονες για να μελετήσει το πρόβλημα. Στο ζήτημα της μονάδας μήκους η άποψη που κυριάρχησε ήταν η νέα μονάδα - για να μπορεί να γίνει παγκόσμια αποδεκτή - να βασίζεται στο μέγεθος του πλανήτη Γη .

Μια ειδική αποστολή ανέλαβε να μετρήσει την απόσταση Δουνκέρκης - Βαρκελώνης πάνω στον μεσημβρινό που περνάει από το Αστεροσκοπείο του Παρισιού .

Η απόσταση μετρήθηκε, ύστερα από οκτώ χρόνια, και, με βάση αυτήν υπολογίστηκε η απόσταση Βόρειου Πόλου – Ισημερινού. Ένα βολικό κλάσμα 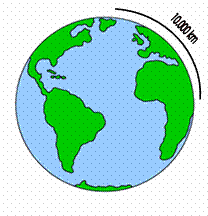αυτής της απόστασης – το ένα προς 10. 000.000, ορίστηκε ως η νέα μονάδα μήκους , ονομάστηκε «ΈΝΑ ΜΕΤΡΟ» και συμβολίζεται με 1 m.

Στα χρόνια που ακολούθησαν όλο και περισσότερες χώρες, ανάμεσά τους και η Ελλάδα, άρχισαν να αποδέχονται το «ένα μέτρο» ως μονάδα μέτρησης .

Εδώ και μερικές δεκαετίες άλλαξε ο τρόπος που ορίζεται από τη Φυσική το ένα μέτρο χωρίς όμως να αλλάξει η «ποσότητα απόστασης» στην οποία αντιστοιχεί.

Χίλια μέτρα μας κάνουν ένα χιλιόμετρο. Το σύμβολο είναι 1 km. Το ένα εκατοστό του μέτρου συμβολίζεται 1 cm και το ένα χιλιοστό 1 mm

Φύλλο εργασίας .

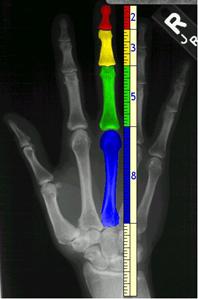Καθένα από τα πέντε δάκτυλα του ανθρώπινου χεριού έχει όνομα. Είναι με τη σειρά, ο αντίχειρας, ο δείκτης, ο μέσος, ο παράμεσος, ο μικρός. Καθένα από τα δάκτυλά μας έχει φάλαγγες. Στην εικόνα εμφανίζεται η ακτινογραφία ενός χεριού.

Χρησιμοποιώντας το υποδεκάμετρο που υπάρχει στο φύλλο εργασίας, σου ζητούμε συγκεντρώνοντας την προσοχή σου στο μεσαίο δάκτυλο

α. να μετρήσεις το μήκος της μεγαλύτερης φάλαγγας αυτού του δάκτυλου, στη συνέχεια

β. να μετρήσεις το μήκος της αμέσως μικρότερης

γ. να διαιρέσεις το μεγαλύτερο μήκος με το μικρότερο. Θα βρεις έτσι «το πόσο είναι μεγαλύτερη η μία φάλαγγα από την άλλη», τον λόγο των δύο μηκών όπως λένε οι μαθηματικοί.

Να καταγράψεις τα αποτελέσματα στον πίνακα που ακολουθεί.

Να επαναλάβεις τα ίδια με το δάκτυλο αριστερά τον δείκτη και να καταγράψεις τα αποτελέσματα στη κάτω στήλη του πίνακα .

Δάκτυλο :	Μήκος 1^η^ς φάλαγγας	Μήκος 2^ηφάλαγγας	Ο λόγος των μηκών
μέσος
δείκτης

Οι μετρήσεις έχουν δείξει ότι, σε όλες τις περιπτώσεις, ο λόγος του μήκους μιας φάλαγγας προς το μήκος της επόμενης είναι πάντοτε ίδιος, για όλα τα ανθρώπινα πλάσματα και είναι ίσος με ένα αριθμό, ο οποίος λέγεται «αριθμός Φιμπονάτσι»². Είναι περίπου 1,62.

1. Σου ζητούμε να συγκρίνεις τα δικά σου αποτελέσματα για τον «λόγο» με τον αριθμό Φιμπονάτσι . Θα βρεις ίσως κάποια διαφορά . Γιατί εμφανίζεται αυτή η διαφορά ; Ποια είναι η γνώμη σου ; .

………………………………………………………………………………………………….................................................................................................................................................................

2. Χρησιμοποιώντας μετροταινία, σου ζητούμε να μετρήσεις το ύψος σου και στη συνέχεια να μετρήσεις την απόσταση από τον αφαλό μέχρι το πάτωμα και να κάνεις τη διαίρεση . Σε ποιο αποτέλεσμα καταλήγεις ; Να καταγράψεις τις τιμές των δύο μετρήσεων και τον λόγο στον οποίο κατέληξες

…………………………………………………………………………………………………................................................................................................................................................................

Ο αριθμός Fibonacci- Φιμπονάτσι, λέγεται και χρυσός αριθμός. Συμβολίζεται με το ελληνικό γράμμα «φ». Σχετίζεται ακόμα και με τις βασικές διαστάσεις της Ακρόπολης και των Πυραμίδων

Ο διδάσκων στην τάξη και ομάδες μαθητών. Τους ζητεί να μετρήσουν τη διάμετρο του κέρματος «ένα ευρώ», χρησιμοποιώντας ένα μόνο κέρμα και υποδεκάμετρο και να καταγράψουν το αποτέλεσμα. Τους καλεί στη συνέχεια να δοκιμάσουν την ίδια μέτρηση χρησιμοποιώντας περισσότερα ( λόγου χάρη τέσσερα), βάζοντάς τα το ένα μετά το άλλο σε σειρά και να κάνουν στη συνέχεια. Τους καλεί να συγκρίνουν τα δυο αποτελέσματα και να εκφράσουν ύστερα από μια σύντομη μεταξύ των κάθε ομάδας συζήτηση μια γνώμη σχετικά με το «ποια μέτρηση έχει μικρότερο σφάλμα». Τους καλεί στη συνέχεια να μετρήσουν το πάχος του ίδιου κέρματος, με υποδεκάμετρο, δοκιμάζοντας εάν η μέτρηση μπορεί να γίνει. με ένα μόνο κέρμα και να σκεφτούν κάτι καλύτερο. Τους παρουσιάζει – εφόσον βέβαια υπάρχει στο σχολείο – το όργανο διαστημόμετρο

5. Η Φυσική χρησιμοποιεί σύμβολα

Ο διδάσκων στην τάξη .Παρουσιάζει, με όσο πιο «μαλακό» τρόπο γίνεται, την πρακτική των φυσικών να χρησιμοποιούν σύμβολα.

Αν μετρήσουν το μήκος ενός μολυβιού και το βρουν 19 εκατοστά τους προτείνει να παριστάνουν το μήκος με το γράμμα ℓ και να γράφουν ℓ = 19 cm

Η παρουσίαση γίνεται με ιδιαίτερη προσοχή .

6. Το μήκος του κύκλου και η ακτίνα του.

Ο διδάσκων ενθαρρύνει την πραγματοποίηση μιας όσο γίνεται ακριβέστερης μέτρησης της διαμέτρου ενός κέρματος « 2 ευρώ» και καταγράφεται το αποτέλεσμα . Είναι γύρω στα 26 mm. Ζητεί από τους μαθητές και τις μαθήτριες να καταγράψουν στο τετράδιο την εκτίμησή τους για το «πόσο είναι το μήκος της περιφέρειας του κέρματος» . Είναι μεγαλύτερο από τη διάμετρο αλλά «πόσες φορές;» Στη συνέχεια ακολουθεί μια μέτρηση του μήκους του κύκλου - με τη βοήθεια νήματος- και καταλήγει σε μία τιμή γύρω στα 82 mm. H τιμή καταγράφεται σε πίνακα και οι μαθητές καλούνται να προσδιορίσουν την απάντηση στο ερώτημα «πόσες φορές το μήκος του συγκεκριμένου κύκλου είναι μεγαλύτερο από τη διάμετρό του». Προκύπτει κάτι γύρω στο 3,15.

Η δραστηριότητα επαναλαμβάνεται με έναν μεγαλύτερο κύκλο, την κυκλική βάση, λόγου χάρη, ενός κυλινδρικού δοχείου. Ο υπολογισμός του «πόσες φορές το μήκος του κύκλου είναι σε αυτή την περίπτωση μεγαλύτερο από τη διάμετρο» οδηγεί σε συζήτηση και σε κάποια συμπεράσματα.

Το μήκος οποιουδήποτε κύκλου «στον Κόσμο» είναι πάντα μεγαλύτερο από τη διάμετρο του ίδιου κύκλου 3,14 φορές περίπου.

Γίνεται αναφορά στον αριθμό «π».

Αν πολλαπλασιάσουμε τη διάμετρο οποιουδήποτε κύκλου επί 3,14 θα έχουμε το μήκος του κύκλου.

Αν πολλαπλασιάσουμε την ακτίνα οποιουδήποτε κύκλου επί 6,28 προκύπτει το μήκος του κύκλου

Υλικό για αξιολόγηση

1.Η Γεωμετρία και η μαθήτρια.

Μια μαθήτρια, βασιζόμενη στον αρχικό ορισμό της μονάδας 1 m και θεωρώντας τη Γη σφαίρα, υποστηρίζει α. ότι το μήκος του Ισημερινού είναι 40.000 km και

β. ότι η ακτίνα της Γης είναι περίπου 6370 km. Έχει δίκιο ; Να δικαιολογήσετε την απάντηση.

2. Απέχουν 23 πόδια ακριβώς.

Ένας μαθητής μετρά με πόδια μια από τις διαστάσεις του πατώματος της σχολικής αίθουσας – απόσταση δύο κατακόρυφων τοίχων- και την βρίσκει 23 πόδια ακριβώς. Τι θα του προτείνατε να κάνει ώστε, διαθέτοντας ένα υποδεκάμετρο, να υπολογίσει πόσα μέτρα απέχουν οι δύο αυτοί κατακόρυφοι τοίχοι ; Πόσο είναι το εμβαδόν της σχολικής αίθουσας ;

3. Ο Λεονάρντο ντα Βίντσι.

Μια μαθήτρια μετρά το ύψος της και βρίσκει 1, 54 m. Τεντώνει, στη συνέχεια, τα χέρια ώστε να γίνουν οριζόντια, μετρά την απόσταση από την άκρη του ενός χεριού μέχρι την άκρη του άλλου, τη βρίσκει 1, 54 m και εντυπωσιάζεται. Θεωρούσε ότι θα έβρισκε την απόσταση αρκετά πιο μικρή. Είναι «κάτι» το οποίο πρώτος είχε διακρίνει ο Λεονάρντο ντα Βίντσι. Σας ζητούμε να κάνετε τις δύο μετρήσεις και για το δικό σας σώμα και να καταγράψετε το αποτέλεσμα .

4. Δέκα «καποδίστριες»

Η Νεφέλη, μαθήτρια της Α΄Γυμνασίου ισχυρίζεται ότι μέτρησε τη διάμετρο ενός κέρματος 1 ευρώ και βρήκε 23 mm, περίπου. Δηλώνει επίσης ότι χρησιμοποίησε 5 κέρματα. Ο Αλέξανδρος, συμμαθητής της ανακοινώνει ότι εκείνος μέτρησε τη διάμετρο ενός κέρματος με τη μορφή του Ιωάννη Καποδίστρια και βρήκε 22 mm, περίπου. Ισχυρίζεται ότι χρησιμοποίησε δέκα «καποδίστριες». Σας ζητούμε α. να μετρήσετε με υποδεκάμετρο τις ίδιες μετρήσεις και κρίνετε εάν οι μαθητές έχουν δίκιο. β. Βασιζόμενοι στις δικές σας μετρήσεις να υπολογίσετε το μήκος της περιφέρειας για κάθε νόμισμα

5. Λιγότερο ή περισσότερο από δύο χιλιοστά ;

Σας ζητούμε, κάνοντας την κατάλληλη μέτρηση, να διαπιστώσετε εάν το πάχος του νομίσματος των 20 λεπτών είναι λιγότερο ή περισσότερο από 2 mm. Na κάνετε το ίδιο για ένα νόμισμα των 10 λεπτών.

6.Το πόδι, η μπάλα, το τραπέζι, η σελίδα του βιβλίου

Σας ζητούμε να μετρήσετε : α. Το πάχος μιας σελίδας βιβλίου. β. Τη διάμετρο μιας μπάλας του μπάσκετ. γ. Το μήκος του δικού σας πέλματος δ. Τις διαστάσεις ενός τραπεζιού στο σπίτι σας και να καταγράψετε τα αποτελέσματα

Παραπομπές

1. Το εγχείρημα του Ερατοσθένη έχει ιδιαίτερο διδακτικό ενδιαφέρον αλλά για να κατανοηθεί χρειάζονται κάποιες γνώσεις Γεωμετρίας αλλά και κατανόηση της δημιουργίας σκιάς της έννοιας «ελάχιστο μέγεθος σκιάς» και όχι μόνο

Είναι προτιμότερο να μην επεκταθούμε στο πώς το κατάφερε αλλά να δώσουμε υπόσχεση ότι στο μέλλον που θα έχουν εμπλουτίσει τις γνώσεις

2. Ο Λεονάρντο Φιμπονάτσι, γεννημένος τον 12^ο αιώνα στην Πίζα της Ιταλίας -λέγεται και Λεονάρντο της Πίζας- ήταν ένας από τους μεγαλύτερους μαθηματικούς του Μεσαίωνα.

Ο αριθμός φ, με προσέγγιση δέκα δεκαδικών ψηφίων, είναι 1,6180339887.... Αν τον βάλουμε στον κομπιουτεράκι και αναζητήσουμε τον αντίστροφό του θα βρούμε τον 0,6180339887. . Διαπιστώνουμε ότι ο αντίστροφός του διαφέρει από αυτόν κατά μια ακριβώς μονάδα. Είναι οι μοναδικοί αριθμοί για τους οποίους συμβαίνει αυτό.

Ισοδύναμα ο φ είναι και ο μοναδικός αριθμός που αν υψωθεί στο τετράγωνο θα αυξηθεί κατά μία ακριβώς μονάδα. Η τιμή του θα προκύπτει από τη λύση της φ - 1 = 1/φ ή φ² = φ +1 Οι δύο λύσεις της δευτεροβάθμιας είναι η (√5)+1)/2 ≈ 1,618. . και η (√5)-1)/2 = 0,618

Στο συγκεκριμένο αρχείο έχει ενσωματωθεί μία εξαιρετική ιδέα του Γιώργου Φασουλόπουλου

Ανδρέας Ιωάννου Κασσέτας