Ανδρέας Ιωάννου Κασσέτας

Διδασκαλία Φυσικής στην Α΄ Γυμνασίου

Μέτρηση του όγκου ενός υλικού σώματος

Η διδασκαλία αλλά και η ιδιαίτερη σημασία της έννοιας « όγκος υλικού σώματος» υποτιμάται σε όλες τις βαθμίδες της εκπαίδευσης

1. Το εμβαδόν μιας επιφάνειας

2. Ο όγκος ενός υλικού σώματος.

3. Μετρώντας όγκο με Γεωμετρία .

4. Η μονάδα όγκου και τα σύμβολα .

5. Η μέτρηση του όγκου σώματος με ογκομετρικό σωλήνα

6. Ο όγκος ενός σώματος μεταβάλλεται ;

1. Το εμβαδόν μιας επιφάνειας

Το εμβαδόν είναι πανάρχαια έννοια της Γεωμετρίας την οποία υιοθέτησε η Φυσική,

Η Φυσική ενδιαφέρθηκε για την έννοια «εμβαδόν της επιφάνειας ενός υλικού σώματος».

Καλούνται οι διδασκόμενοι να μετρήσουν το εμβαδόν του πατώματος της σχολικής

Γίνεται μέτρηση των δύο διαστάσεων και στη συνέχεια οι μαθητές ενθαρρύνονται να θυμηθούν ότι το εμβαδόν ενός ορθογωνίου παραλληλογράμμου προσδιορίζεται εάν πολλαπλασιάσουμε τις δύο διαστάσεις του. Εάν το πάτωμα της σχολικής αίθουσας έχει διαστάσεις 5 μέτρα και 6 μέτρα το εμβαδόν θα είναι 30 τετραγωνικά μέτρα.

Με βάση τη μονάδα «ένα μέτρο μήκους» δημιουργήθηκε

και η μονάδα μέτρησης «ένα τετραγωνικό μέτρο» για το εμβαδόν κάθε επιφάνειας. - το εμβαδόν ενός τετραγώνου πλευράς ενός μέτρου. Η μονάδα «ένα τετραγωνικό εκατοστό» είναι το εμβαδόν ενός τετραγώνου πλευράς 1 cm.

Οι μαθητές και οι μαθήτριες διδάσκονται¹ τους συμβολισμούς 3 x 3 = 3² , α x α = α²

1 m x 1 m = 1 m² και 1 cm x 1 cm = 1 cm²

Για το εμβαδόν της αίθουσας καλούνται να γράψουν 5 m x 6 m = 30 m².

Στους μαθητές και στις μαθήτριες υπενθυμίζεται ότι αν το σχήμα είναι κύκλος το εμβαδόν είναι ίσο με «ακτίνα επί ακτίνα x 3,14».

Ζητείται να μετρηθεί το εμβαδόν της επιφάνειας ενός κέρματος.

2. Ο όγκος ενός υλικού σώματος²

O «όγκος ενός γεωμετρικού στερεού » είναι πανάρχαια έννοια της Γεωμετρίας

η οποία αξιοποιήθηκε από τη Φυσική. Η Φυσική ενδιαφέρθηκε ειδικά για την έννοια «όγκος ενός υλικού σώματος» είτε αυτό έχει το περίπου σφαιρικό σχήμα ενός ροδάκινου, είτε έχει το σχήμα μιας πατάτας, είτε έχει το σχήμα μιας ποσότητας αέρα μέσα στο δοχείο της. Ωστόσο όλες οι μετρήσεις για τον όγκο ενός στερεού ανάγονται τελικά στη Γεωμετρία. Μετρώντας τον όγκο ενός βότσαλου με ογκομετρικό σωλήνα, επί της ουσίας μετράμε τον όγκο της ποσότητας νερού που «ανέβηκε» με το βύθισμα του βότσαλου και η ποσοτητα αυτή νερού έχει το κυλινδικό σχήμα του δοχείου .

Τα στερεά και τα υγρά σώματα . Στη Φυσική κάθε στερεό αντικείμενο, σε ορισμένη θερμοκρασία, εφόσον παραμένει στερεό αντικείμενο, έχει έναν ορισμένο όγκο. Το ίδιο θεωρείται ότι ισχύει και για κάθε υγρό σώμα, όπως είναι το νερό. Εφόσον διατηρείται σε σταθερή θερμοκρασία και παραμένει σε υγρή κατάσταση έχει ορισμένο όγκο.

3. Μετρώντας όγκο με Γεωμετρία .

Οι μαθητές καλούνται να μετρήσουν τον όγκο του αέρα της αίθουσας με δεδομένο τις τιμές των τριών διαστάσεων. Αν φανεί ότι η μέτρηση δεν μπορεί να «προχωρήσει» ο διδάσκων αποφαίνεται ότι για ένα σχήμα όπως αυτό της αίθουσας

ο όγκος υπολογίζεται με το να πολλαπλασιάσουμε το εμβαδόν του πατώματος επί το ύψος. Αν το πάτωμα έχει διαστάσεις 5 μέτρα και 6 μέτρα, το εμβαδόν είναι 30 τετραγωνικά μέτρα

και αν το ύψος της αίθουσας είναι 4 μέτρα ο όγκος του αέρα θα 120 κυβικά μέτρα .

Ζητείται από τους μαθητές να υπολογίσουν τον όγκο που έχει ένα κυβικό αντικείμενο με

πλευρά 1 εκατοστό.

4. Η μονάδα όγκου και τα σύμβολα .

Η μονάδα όγκου «ένα κυβικό μέτρο» δημιουργήθηκε με βάση τη μονάδα «ένα μέτρο μήκους».

Ένα κυβικό μέτρο θεωρείται ο όγκος ενός κύβου πλευράς ενός μέτρου .

Οι μαθητές και οι μαθήτριες διδάσκονται να γράφουν με σύμβολα την ισότητα

1 m x 1 m x 1 m = 1 m³ Το ένα κυβικό μέτρο συμβολίζεται με 1 m³

Αντίστοιχα ο όγκος ενός κύβου πλευράς ενός εκατοστού είναι ένα κυβικό εκατοστό

1 cm x 1 cm x 1 cm = 1 cm³ Το κυβικό εκατοστό συμβολίζεται με 1 cm³

Το 1/1000 της μονάδας «ένα κυβικό μέτρο» έχει επικρατήσει να λέγεται ένα λίτρο . Συμβολίζεται με 1ℓ και είναι ο όγκος ενός κύβου πλευράς 10 cm.

Ένα λίτρο είναι ίσο με 1000 κυβικά εκατοστά τα οποία λέγονται μιλιλίτρ και συμβολίζονται με mℓ. 1 mℓ = 1 cm³ .

Το σύμβολο για τον όγκο ενός σώματος είναι το κεφαλαίο V.

Αν ένα υλικό σώμα έχει όγκο 3 κυβικών μέτρων γράφουμε V = 3 m³.

Οι διδασκόμενοι καλούνται να αναζητήσουν και στο επόμενο μάθημα να παρουσιάσουν τις τιμή α. του όγκου νερού σε μια μεγάλη πλαστική φιάλη και σε μια μικρή πλαστική φιάλη νερού β. τον όγκο του αναψυκτικού σε μια μεταλλική γ. του όγκου του κρασιού σε ένα μπουκάλι κρασί.

Οι μαθητές σε ομάδες και ο διδάσκων μοιράζει σε κάθε ομάδα ένα μεταλλικό κουτί από αναψυκτικό και υποδεκάμετρο και καλεί τους μαθητές να φανταστούν πώς μπορεί να υπολογιστεί του αντικειμένου .

Παρουσιάζει το ζήτημα έτσι ώστε να εκμαιεύσει την ερώτηση «μήπως ο όγκος του κυλίνδρου υπολογίζεται με το να πολλαπλασιάσουμε το εμβαδόν της βάσης επί το ύψος;». Αν δεν την εκμαιεύσει το παρουσιάζει .

Οι μαθητές κάθε ομάδας συνεργάζονται και κάθε ομάδα καταλήγει σε ένα δικό της συμπέρασμα το οποίο και ανακοινώνει. Το κουτί θα μπορούσε να είναι 330 mℓ και να γίνει η σύγκριση του αποτελέσματος της μέτρησης με το δεδομένο 330 mℓ .

Ο όγκος δεν μεταβάλλεται. Αν βάλουμε μια ντομάτα 300 κυβικών εκατοστών σε νερό 500 κυβικών εκατοστών, το σύνολο «νερό και βυθισμένη ντομάτα» θα έχει όγκο 800 κυβικών εκατοστών ακριβώς.

5. Η μέτρηση του όγκου με ογκομετρικό σωλήνα

Ο διδάσκων δίνει στην ομάδα μαθητών αντικείμενα που θα βούλιαζαν στο νερό και προμηθεύει την ομάδα με βαθμολογημένο ογκομετρικό σωλήνα με νερό και ζητεί να μετρήσουν τον όγκο κάθε αντικειμένου.

Αν το αντικείμενο έχει τυχαίο σχήμα – όπως λόγου χάρη μια πέτρα – μπορούμε να μετρήσουμε τον όγκο του βυθίζοντάς το σε ογκομετρικό σωλήνα με νερό.

Η μέτρηση βασίζεται στην παραδοχή ότι με τη βύθιση του αντικειμένου στο νερό ο όγκος τόσο του νερού όσο και του αντικειμένου παραμένει ίδιος και :

όγκος νερού + όγκος πέτρας = όγκος του συνόλου «νερό και βυθισμένη πέτρα»

H εμπειρία. Σε ευρύτερο ογκομετρικό σωλήνα βάζουμε νερό μέχρι την ένδειξη 400 ml, βυθίζουμε στη συνέχεια ένα μανταρίνι. Καθώς το μανταρίνι ανέρχεται διαβάζουμε την ένδειξη 630 ml και βγάζουμε το συμπέρασμα για τον όγκο του. Όγκος νερού + όγκος μανταρινιού = όγκος του συνόλου «νερό και μανταρίνι»

6. Σε ορισμένες περιπτώσεις³ ο όγκος μεταβάλλεται.

Η εμπειρία. Ένα μπουκάλι γεμάτο με νερό στην κατάψυξη. Όταν το νερό παγώσει το μπουκάλι μπορεί ακόμα και να σπάσει.

Η σκέψη. Όταν το νερό παγώνει ο όγκος του πάγου θα είναι μεγαλύτερος.

Η εργαστηριακή εμπειρία. Η μεταλλική σφαίρα περνάει μέσα από τον δακτύλιο.

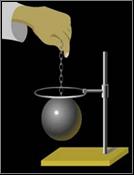Τη θερμαίνει και δεν χωράει

να περάσει μέσα από τον ίδιο δακτύλιο

Η σκέψη.

Όταν μια μεταλλική σφαίρα θερμαίνεται

αυξάνεται ο όγκος της.

Η εμπειρία- μνήμη. Ένα θερμόμετρο με υδράργυρο. Όταν κάνει ζέστη ο υδράργυρος «ανεβαίνει».

Η σκέψη. Όταν ο υδράργυρος θερμαίνεται, αυξάνεται ο όγκος του περισσότερο από όσο αυξάνεται ο όγκος του γυάλινου περιβλήματος.

Υλικό για αξιολόγηση.

1. Ο όγκος του αόρατου αέρα

Με μετροταινία μετρήθηκαν οι διαστάσεις του δαπέδου της σχολικής αίθουσας και βρέθηκαν 6,7 m και 5 m, ενώ το ύψος εκτιμήθηκε ότι είναι 3,5 m. Με βάση τα στοιχεία αυτά σας ζητούμε α. Να υπολογίσετε, σε τετραγωνικά μέτρα το εμβαδόν του δαπέδου και το εμβαδόν της επιφάνειας καθενός από τους τοίχους. β. Να υπολογίσετε σε κυβικά μέτρα τον όγκο του.

Παραπομπές

1. Οι μαθητές έχουν ήδη διδαχθεί στο Δημοτικό σχολείο τον συμβολισμό 3² για το τετράγωνο του αριθμού όπως, λόγου χάρη το 3. Αυτό δεν σημαίνει ότι όλοι το έχουν μάθει. Ο διδάσκων οφείλει να παρουσιάσει τον συμβολισμό 1 m² πολύ προσεκτικά.

2. Η έννοια ΟΓΚΟΣ ως πανάρχαια έννοια της Γεωμετρίας αναφέρεται σε ΓΕΩΜΕΤΡΙΚΟ ΣΤΕΡΕΟ. Πολύ πριν από την εμφάνιση την εμφάνιση της Φυσικής η Τεχνολογία είχε χρησιμοποιήσει την έννοια «όγκος ενός σώματος» και διέθετε και μονάδες μέτρησης.

Για τη Φυσική η συνώνυμη έννοια αναφέρεται σε ΥΛΙΚΟ ΣΩΜΑ είναι «ΟΓΚΟΣ ΤΟΥ ΣΩΜΑΤΟΣ» και συνιστά πρωταρχική ιδιότητα κάθε υλικού σώματος. Για τον Isaac Newton ( Principia ) ένα σώμα θεωρείται υλικό σώμα εφόσον «διαθέτει» ΟΓΚΟ και ΑΔΡΑΝΕΙΑ. Για να προσδιορίσει ωστόσο την ποσότητα της ύλης – τη θεωρούμενη ως μάζα - καταφεύγει στην ιδιότητα «αδράνεια».

Η «ποσότητα όγκου» ενός υλικού σώματος είναι ίση με τον όγκο του αντίστοιχου – μη υλικού – γεωμετρικού στερεού της Γεωμετρίας .

3. Στο φαινόμενο «θερμική διαστολή» θα βασιστεί αργότερα και η μέτρηση της θερμοκρασίας

Ανδρέας Ιωάννου Κασσέτας