Ανδρέας Ιωάννου Κασσέτας

Διδασκαλία Φυσικής στην Α΄ Γυμνασίου

Η μέτρηση της μάζας.

Υλικό για 3ωρη διδασκαλία. Υλικό για αξιολόγηση

· Η εμπειρία – μνήμη. Η εργαστηριακή εμπειρία. Το «καλύτερο» πείραμα. Το «τρίπτυχο».

· Να μετρήσουμε τη μάζα. Μια μονάδα μέτρησης για όλους τους λαούς.

· Η μάζα και ο όγκος ενός σώματος.

· Μάζα έχουν ακόμα και τα «φαντάσματα»; Τι συμβαίνει με τον «αόρατο» αέρα; Έχει μάζα ; Έχει και βάρος ;

· Η μάζα και η θερμοκρασία ενός σώματος

· Η μάζα και το βάρος. Το ελατήριο. Να μετρήσουμε το βάρος

Υλικό για αξιολόγηση

1. Η εμπειρία-μνήμη.

« Όσα παίρνει ο άνεμος»

Όταν φυσήξει, ο άνεμος «παίρνει» τα φύλλο από χαρτί που είχαμε αφήσει πάνω στο τραπέζι,

παίρνει και τα φύλλα του φθινόπωρου, δεν «παίρνει» το κρυστάλλινο βάζο ούτε τον θρανίο¹, ούτε τον καναπέ. Παίρνει εκείνα που αντιστέκονται λιγότερο. Παίρνει εκείνα με τη μικρότερη ΜΑΖΑ, λένε οι φυσικοί .

Το τούβλο και το φύλλο της βελανιδιάς

Η εμπειρία μας διδάσκει ότι ένα σώμα όπως το τούβλο

αντιστέκεται στη μετακίνησή του περισσότερο από ένα φύλλο βελανιδιάς.

Έχει μεγαλύτερη μάζα λένε οι φυσικοί.

Μας διδάσκει, όμως, και κάτι άλλο:

Ότι το τούβλο είναι βαρύτερο

από το φύλλο της βελανιδιάς.

2. Η εργαστηριακή εμπειρία και το «τρίπτυχο»

Το καλύτερο πείραμα.

Στο σχολικό εργαστήριο. Δύο όμοια τενεκεδένια κουτιά κρεμασμένα από δύο διαφορετικά αλλά ισομήκη νήματα και ο διδάσκων δηλώνει 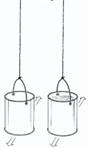ότι το ένα είναι άδειο, το άλλο γεμάτο με άμμο.

Κάθε μαθητής και κάθε μαθήτρια καλείται να επινοήσει έναν τρόπο ώστε να βρει ποιο είναι το γεμάτο χωρίς να κοιτάξει «μέσα» σε κάθε κουτί

Μια ιδέα είναι «να σπρώξει» ο διδασκόμενος το κάθε κουτί με το χέρι ώστε να διαπιστώσει ποιο αντιστέκεται περισσότερο ΑΙΣΘΗΤΗΡΙΑΚΗ ΕΜΠΕΙΡΙΑ . Το γεμάτο κουτί είναι εκείνο που αντιστέκεται περισσότερο σε ένα σπρώξιμο .

Αφού διαπιστωθεί ότι το κουτί Α είναι το γεμάτο με άμμο, καλείται ο διδασκόμενος να εκτιμήσει ποιο από τα δύο είναι βαρύτερο μέσα από ΑΙΣΘΗΤΗΡΙΑΚΗ ΕΜΠΕΙΡΙΑ, πιάνοντας κάθε κουτί από κάτω ώστε να στηρίζεται στο χέρι του χωρίς το νήμα να είναι τεντωμένο, δοκιμάζοντας να το σηκώσει έστω και λίγο. Ήταν αναμενόμενο αλλά επιβεβαιώνεται εμπειρικά ότι «το γεμάτο κουτί είναι εκείνο που αντιστέκεται περισσότερο σε ένα σπρώξιμο»

Η ανάγνωση των εμπειρικών δεδομένων. Το «τρίπτυχο»

α. Η αντίσταση- δυσφορία στη μετακίνηση είναι – γενικώς – για κάθε σώμα διαφορετική

β. Το σώμα που εκδηλώνει μεγαλύτερη δυσφορία έχει και μεγαλύτερο βάρος

γ. Το σώμα που εκδηλώνει μεγαλύτερη δυσφορία εμπεριέχει και περισσότερο υλικό.

Το τρίπτυχο:

1. ΑΝΤΙΣΤΕΚΕΤΑΙ ΠΕΡΙΣΣΟΤΕΡΟ

2. ΕΙΝΑΙ ΒΑΡΥΤΕΡΟ

2. ΕΧΕΙ ΠΕΡΙΣΣΟΤΕΡΟ ΥΛΙΚΟ.

είναι στο επίκεντρο της διδασκαλίας και επαναλαμβάνονται οι αναφορές σε αυτό σε όλη τη διάρκεια της διδασκαλίας.

Ο διδάσκων εστιάζει στο τρίπτυχο και , σε κάποιο βαθμό , γενικεύει

α. Η αντίσταση- δυσφορία που εκδηλώνει ένα σώμα σε κάθε απόπειρα για τη μετακίνησή του περιγράφεται από τη Φυσική με την έννοια «μάζα του σώματος²»

β. Η μάζα κάθε σώματος είναι ανάλογη προς το βάρος του. Ένα σώμα με διπλάσιο βάρος από ένα άλλο, έχει και διπλάσια μάζα.

γ. Ένα σώμα με μεγαλύτερη μάζα από ένα άλλο εμπεριέχει και περισσότερη ύλη.

Το πείραμα με τα δύο κρεμασμένα εξωτερικά όμοια κουτιά – θα μπορούσε να είναι και δύο μπουκάλια καλυμμένα ώστε να είναι αδιαφανή- είναι ΠΑΡΑΔΟΣΙΑΚΟ αλλά και συγχρόνως είναι και το , κατά την άποψή μου, ΚΑΛΥΤΕΡΟ για μία πρώτη γνωριμία με την έννοια μάζα.

Η εμπειρία «όσα παίρνει ο άνεμος» εμπεριέχει το μειονέκτημα ότι παρεμβαίνει και η τιμή του συντελεστή στατικής τριβής, ενώ το συγκεκριμένο πείραμα η τιμή του συντελεστή τριβής δεν επηρεάζει τις εξελίξεις.

Μέσα στην τάξη. Δύο σφαίρες ίδιου μεγέθους και χρώματος από διαφορετικό υλικό τοποθετημένες σε οριζόντια επιφάνεια. Οι μαθητές καλούνται να επιχειρήσουν να κυλήσουν γρήγορα τις δύο σφαίρες μπρος πίσω, είτε με το χέρι είτε φυσώντας με καλαμάκι. Διαπιστώνεται ότι η μία σφαίρα εκδηλώνει μεγαλύτερη δυσφορία από την άλλη στην επιδιωκόμενη μετακίνησή της. Διαπιστώνεται επίσης – κρατώντας τις δύο σφαίρες μία σε κάθε χέρι - ότι η σφαίρα που εκδηλώνει μεγαλύτερη δυσφορία είναι και η βαρύτερη.

Εάν σχετικό μειονέκτημα του πειράματος είναι ότι πρέπει να βρεθούν ή να δημιουργηθούν δύο μπίλιες ίδιου μεγέθους από διαφορετικό υλικό, λόγου χάρη, η μία από ατσάλι, η άλλη από γυαλί.

Σε σχέση με το πείραμα με τα «δύο κρεμασμένα κουτιά από αναψυκτικό» το μειονέκτημα είναι ότι ο διδασκόμενος δεν μπορεί να διαπιστώσει πως η μπίλια που αντιστέκεται περισσότερο και είναι συγχρόνως η βαρύτερη εμπεριέχει και περισσότερο υλικό.

3. Να μετρήσουμε τη μάζα.

Η διδασκαλία εστιάζει στη μία από τις διαπιστώσεις εκείνη που έδειξε ότι το σώμα που αντιστέκεται περισσότερο είναι και το πιο βαρύ και παρουσιάζεται χωρίς απόδειξη η ΑΝΑΛΟΓΙΑ «η μάζα κάθε σώματος είναι ανάλογη με το βάρος του». Αν το βάρος ενός σώματος Α είναι τριπλάσιο από το βάρος ενός άλλου σώματος και η μάζα του Α θα είναι τριπλάσια από τη μάζα του Β. Μπορούμε συνεπώς να συγκρίνουμε τις μάζες δύο σωμάτων με το να τα ζυγίσουμε. Όργανο για τη μέτρηση της μάζας ο ζυγός3 του εργαστηρίου βαθμολογημένος σε μονάδες μάζας.

Προς το παρόν η έννοια βάρος περιορίζεται στην εμπειρία-μνήμη για το ότι ορισμένα αντικείμενα είναι πιο βαριά από άλλα και στην καθημερινή εμπειρία του ζυγίζω.

Η εμπειρία. Εκτίμηση και στη συνέχεια μέτρηση. Διεργασίες μεταγνώσης.

Στο σχολικό εργαστήριο ή και μέσα στην τάξη . Ο διδάσκων

α. Δίνει σε όλους τους μαθητές να κρατήσουν στο χέρι το ίδιο αντικείμενο ( λόγου χάρη μια μπαταρία πλακέ 4,5 βολτ ή ένα μανταρίνι ) και να ζητεί από καθένα να καταγράψει στο φύλλο εργασίας την εκτίμησή του για τη μάζα του αντικειμένου σε γραμμάρια.

β. Δηλώνει στη συνέχεια ότι η μάζα ενός αυγού είναι 60 περίπου γραμμάρια και ζητεί από τους μαθητές να αλλάξουν ή να διατηρήσουν την εκτίμησή τους

γ. Αναθέτει σε δύο μαθητές να ζυγίσουν το αντικείμενο με εργαστηριακό ζυγό και να ανακοινώσουν το αποτέλεσμα. Καλεί όλους τους μαθητές να καταγράψουν την τιμή αυτή και να σχολιάσουν τη διαφορά ανάμεσα στις προηγούμενες εκτιμήσεις τους και σε αυτό που έδωσε η μέτρηση. Διεργασίες μεταγνώσης.

4. Μια μονάδα μέτρησης για όλους τους λαούς.

Εκτός από το «Ελευθερία, Ισότητα, Αδελφότητα» η Γαλλική Επανάσταση «πρόσφερε» και μονάδες μέτρησης για όλους τους λαούς. Οι Γάλλοι, όταν είχε επικρατήσει η Επανάσταση, αφού πρότειναν την μονάδα «ένα μέτρο», προχώρησαν και σε πρόταση για μία μονάδα μάζας. Θα μπορούσαμε να φανταστούμε ότι έφτιαξαν έναν κύβο με πλευρά 10 cm, τον όγκο του τον ονόμασαν «ένα λίτρο», τον γέμισαν με νερό και πρότειναν ότι η μάζα του νερού όγκου ενός λίτρου³ θα λέγεται “ένα κιλογκράμ”, ένα χιλιόγραμμο, ένα κιλό.

Το ένα χιλιόγραμμο συμβολίζεται με ”1 kg”. Ένα κιλό είναι η μάζα του νερού σε φιάλη του ενός λίτρου. Το ένα χιλιοστό του χιλιογράμμου είναι το ένα γραμμάριο. Συμβολίζεται με ”1 g”.

Ένα σύμβολο για τη μάζα. Το σύμβολο που έχει επικρατήσει για τη μάζα είναι το “m”. Αν ένα σώμα έχει μάζα 120 γραμμαρίων γράφουμε m = 120 g,

5. Η μάζα και ο όγκος

Η διδασκαλία αλλά και η ιδιαίτερη σημασία της έννοιας « όγκος σώματος» υποτιμάται σε όλες τις βαθμίδες της εκπαίδευσης

Ένα κιλό σίδερο κι ένα κιλό βαμβάκι

Από τη μια το σίδερο, από την άλλη το βαμβάκι. Οι συναντήσεις τους όχι και τόσο συχνές , εκτός αν κάποιος – σπάνια ο μπαμπάς – σιδερώνει το πουκάμισο και τα πουκάμισο είναι βαμβακερό.

Ποιο ζυγίζει περισσότερο «ένα κιλό σίδερο ή ένα κιλό μπαμπάκι; » Είναι μια από τις ερωτήσεις που μας έκαναν όταν ήμασταν μικρά παιδιά και συνεχίζουμε να την κάνουμε σε μικρά παιδιά τώρα που έχουμε μεγαλώσει

Αυτό που συμβαίνει είναι ότι ένα κιλό σίδερο έχει την ίδια μάζα και το ίδιο βάρος με ένα κιλό βαμβάκι, αλλά είναι πιο «ογκώδες». Ο όγκος του⁴ είναι μεγαλύτερος λένε οι φυσικοί. Όταν τα αντικείμενα είναι συμπαγή στερεά λέγοντας ότι «το ένα είναι μεγαλύτερο από το άλλο», εννοούμε ότι «έχει μεγαλύτερο όγκο».

Κάθε αντικείμενο, σε μια συγκεκριμένη χρονική στιγμή, έχει ορισμένη μάζα και ορισμένο όγκο. Μια ποσότητα νερού μάζας 1 kg έχει όγκο ενός λίτρου – 1000 cm³ , αλλά ένα κομμάτι σίδερο μάζας με την ίδια μάζα έχει όγκο γύρω 127 cm³, είναι οκτώ περίπου φορές «μικρότερο». Ένα κομμάτι γυαλί με μάζα 1 kg έχει όγκο 370 cm³ , είναι πιο «μεγάλο» από το σιδερένιο κομμάτι του ενός κιλού, και έχει μικρότερο όγκο από ένα κιλό νερού. Με το δεδομένο των μετρήσεων ότι ένα κομμάτι σίδερο με μάζα 1 kg ή 1000 γραμμάρια έχει όγκο 127 κυβικά εκατοστά μπορούμε να υπολογίσουμε «πόση μάζα έχει το ένα κυβικό εκατοστό». Θα κάνουμε ΔΙΑΙΡΕΣΗ. Προκύπτει ότι κάθε κυβικό εκατοστό έχει μάζα γύρω στα 7,8 γραμμάρια. Στη γλώσσα της Φυσικής λέμε ότι η πυκνότητα του σιδήρου είναι 7,8 γραμμάρια σε κάθε κυβικό εκατοστό και γράφουμε ρ = 7,8 g/cm³ . Αντίστοιχα, εφόσον μια ποσότητα νερού με μάζα 1000 g ( 1 kg) έχει όγκο 1000 cm³ λέμε ότι η πυκνότητα του νερού είναι ένα γραμμάριο σε κάθε κυβικό εκατοστό και γράφουμε ρ = 1 g/cm³

http://digitalschool.minedu.gov.gr/modules/document/file.php/DSGYM-B200/ExperimentsBGYM/bG/bG.html

του Ηλία Σιτσανλή .Μέτρηση της πυκνότητας. Είναι εξαιρετικό

Σχόλιο. Η προσέγγιση αυτή , μέσα από μορφές καθοδηγούμενης ανακάλυψης που θα βασίζονται στη ΔΙΑΙΡΕΣΗ είναι προτιμότερη από το να ξεκινήσουμε με το «πυκνότητα λέγεται το πηλίκο . . . .»

6. Ο «αόρατος» αέρας. Έχει μάζα; Έχει βάρος;

Ορισμένα από τα σώματα του «Κόσμου» είναι αόρατα. Ανάμεσά τους, το διασημότερο φάντασμα της Βιόσφαιρας, είναι το σώμα «αέρας»,

ο μεγάλος πρωταγωνιστής. Όταν φυσάει⁵, «κάτι πάντων συμβαίνει» και μας κάνει να υποψιαζόμαστε για την παρουσία κάποιου «φαντάσματος», αλλά μόνο όταν φυσάει. Ωστόσο, ακόμα κι αν δεν φυσάει ο αέρας στέλνει μηνύματα που μας κάνουν να πιστεύομε ότι υπάρχει, αόρατος και αινιγματικός.

Ο διδάσκων αναφέρεται στον «αόρατο» αέρα και μοιράζει φύλλα εργασίας με ερωτήματα για τη μάζα του αέρα που βρίσκεται στη σχολική αίθουσα.

Οι μαθητές και οι μαθήτριες καλούνται να επιλέξουν μία απάντηση στα δύο πρώτα ερωτήματα του φυλλαδίου που παρατίθεται πιο κάτω.

Αφού καταγράψουν τις απαντήσεις στα δύο πρώτα ερωτήματα, ο διδάσκων ζητεί να υπολογίσουν τον όγκο μιας αίθουσας με διαστάσεις τις οποίες παρουσιάζει χρησιμοποιώντας ακέραιους που να είναι «εύκολοι» για τον πολλαπλασιασμό. Οι τιμές λόγου χάρη 7 m x 5 m x 4 m. Οδηγούν σχετικά εύκολα στο 140 m³.

Μετά τον υπολογισμό του «πόσα κυβικά είναι η αίθουσα» πληροφορεί τους μαθητές ότι οι μετρήσεις έχουν δείξει πώς ότι ένα λίτρο αέρα έχει μάζα 1,3 g ή ότι ένα κυβικό μέτρο αέρα έχει μάζα 1,3 kg και τους ζητεί να συμπληρώσουν στο φύλλο εργασίας.

Μετά από τη συζήτηση στην τάξη οι σωστές απαντήσεις είναι . . .

Και η μάζα του αέρα μιας αίθουσας 7 m x 5 m x 4 m είναι γύρω στα 182 kg.

Φύλλο εργασίας

1. Η μάζα του αέρα στην τάξη είναι κατά τη δική μου εκτίμηση

α. Μηδέν β. Γύρω στα 5 γραμμάρια

γ. Γύρω στα 80 γραμμάρια ;

δ. Γύρω στο 1 kg

ε. Περισσότερο από 2 kg;

2. Ο αέρας στη σχολική αίθουσα

α. Έχει βάρος μεγαλύτερο από το βάρος ενός μήλου;

β. Έχει βάρος μικρότερο από το βάρος ενός μήλου ;

γ. Δεν έχει βάρος ;

3. Μετά από τη συζήτηση στην τάξη οι σωστές απαντήσεις είναι . . .

4. Μετά από τη συζήτηση στην τάξη η μάζα του αέρα μιας αίθουσας 7 m x 5 m x 4 m είναι . . . .

Εναλλακτικά θα μπορούσε να προτείνει τη μέτρηση των διαστάσεων της «δικής τους τάξης» παρέχοντας μέτρο «σπαστό» και μετροταινία και να προχωρήσει σε μέτρηση της μάζας του αέρα της συγκεκριμένης τάξης

Είναι δεκάδες οι σχετικές έρευνες που καταδεικνύουν ότι, σε όλες κοινωνίες, οι μαθητές αυτής της ηλικίας πιστεύουν ότι «ο αέρας δεν έχει βάρος» σε ποσοστά πάνω από 60%. Εξάλλου κύλησαν αιώνες με τους στοχαστές να πιστεύουν ότι ο αέρας δεν έχει βάρος. Μόνο όταν επινοήθηκε τρόπος να δημιουργηθεί «χώρος δίχως αέρα» - το «κενό» όπως το έλεγαν – με την αντλία κενού η ιδέα ότι ο αέρας έχει βάρος άρχισε να ερευνάται και μόνο όταν οι ερευνητές του 18^ου αιώνα άρχισαν να «ζυγίζουν» τον αέρα και τα άλλα αέρια , η Χημεία ξεκίνησε για να γίνει τελικά «επιστήμη». Το ότι ο αέρας μιας αίθουσας μπορεί να είναι 150 κιλά εντυπωσιάζει τον οποιονδήποτε κι αυτό και η σχετική διδασκαλία πρέπει να κινηθεί σε μονοπάτια κονστρουκτιβισμού. Με λόγια διαφορετικά, η διδασκαλία μας οφείλει να μην είναι στο στιλ του «Καλημέρα παιδιά . . . ο αέρας έχει βάρος»

7. Η μάζα και η θερμοκρασία

Τι θα συμβεί αν ζεστάνουμε ένα σώμα; Θα αλλάξει η μάζα του ; Θα αλλάξει ο όγκος του ;

Η εργαστηριακή εμπειρία. Ζυγίζει τη μικρή σιδερένια σφαίρα, στη συνέχει τη θερμαίνει και αφού την πιάσει με λαβίδα ώστε να μην «καεί» , την ξαναζυγίζει. Παρατηρεί ότι η ζυγαριά δείχνει το ίδιο.

Η σκέψη. Όταν θερμαίνεται η σφαίρα δεν αλλάζει η μάζα της

Ο διδάσκων ενημερώνει τους μαθητές του ότι όλες οι μετρήσεις που έχουν γίνει δείχνουν αυτό που συνέβη και με το πείραμα. Ότι οποιοδήποτε σώμα και να θερμάνουμε η μάζα του διατηρείται ίδια⁷. Το ίδιο συμβαίνει και όταν ψύχουμε το σώμα.

Η εργαστηριακή εμπειρία. Η μεταλλική σφαίρα περνάει μέσα ένα τον δακτύλιο.

Ο μαθητής την θερμαίνει και δεν χωράει να περάσει μέσα από τον ίδιο δακτύλιο

[

Η σκέψη. Όταν μια μεταλλική σφαίρα θερμαίνεται αυξάνεται ο όγκος της.

Ο καθηγητής ενημερώνει τους μαθητές του ότι «όλες οι μετρήσεις που έχουν γίνει – και όχι μόνο αυτή που γίνεται στο εργαστήριο - δείχνουν ότι όταν θερμαίνουμε ένα σώμα αυξάνεται ο όγκος του, ενώ με την ψύξη ελαττώνεται ο όγκος.

Μια μικρή «ανωμαλία» παρουσιάζει το νερό».

8. Η μάζα και το βάρος

Τι σημαίνει «βάρος» σύμφωνα με τη Φυσική ;

Η πανάρχαια εμπειρία. Κρατάμε στο χέρι ένα αντικείμενο . Όταν το αφήσουμε κινείται προς το έδαφος, πέφτει.

Μια ιδέα του 17^ου αιώνα. Η Γη «τραβά» όλα τα σώματα προς το μέρος της

Μια ακόμα ιδέα . Η δύναμη είναι μια έννοια που περιγράφει τόσο το «σπρώχνω», όσο και το «τραβώ».

Η εμπειρία. Όταν κρεμάσουμε ένα αντικείμενο σε ελατήριο, το ελατήριο τεντώνει και τραβά το αντικείμενο προς το μέρος του . Στη γλώσσα της Φυσικής λέμε «το ελατήριο ασκεί δύναμη στο αντικείμενο» . Όταν συμπιέζουμε ένα ελατήριο με το χέρι μας, ελατήριο συσπειρώνεται γίνεται μικρότερο σε μήκος και σπρώχνει το χέρι μας. Στη γλώσσα της Φυσικής λέμε «το ελατήριο ασκεί δύναμη στο αντικείμενο» .

http://digitalschool.minedu.gov.gr/modules/document/file.php/DSGYM-B200/ExperimentsBGYM/bG/bG.html Ηλίας Σιτσανλής. Η έννοια δύναμη

Στη γλώσσα της Φυσικής. Η Γη τραβά ένα σώμα Σ προς το μέρος της. Στη γλώσσα της Φυσικής λέμε: « . Η Γη ασκεί δύναμη στο σώμα Σ, με κατεύθυνση προς το έδαφος». Τη δύναμη αυτή τη λέμε « βάρος του σώματος Σ».

Ηλίας Σιτσανλής http://digitalschool.minedu.gov.gr/modules/document/file.php/DSGYM-B200/ExperimentsBGYM/bG/bG.html Ηλίας Σιτσανλής. Το βάρος ως δύναμη

9. Πώς θα μετρήσουμε το βάρος ;

Το ελατήριο. Ένα αντικείμενο πολύτιμο για την εξέλιξη της Φυσικής

Τα εκκρεμή και τα ελατήρια είναι ΑΝΤΙΚΕΙΜΕΝΑ που βοήθησαν ιδιαίτερα τους ερευνητές στο να οικοδομήσουν τη Φυσική

Στο σχολικό εργαστήριο. Φύλλο εργασίας και ένα κατακόρυφο ελατήριο μήκους στερεωμένο στο ανώτερο άκρο του. Οι μαθητές μετρούν το μήκος, βρίσκουν ότι είναι – ας υποθέσουμε - 22 cm και καταγράφουν την τιμή στο φύλλο εργασίας, Κρεμούν στη συνέχεια ένα βαρίδι 100 γραμμαρίων και κάνοντας τη μέτρηση βρίσκουν ότι το μήκος του ελατηρίου έχει γίνει 23 cm. Στην πρώτη στήλη καταγράφουν την τιμή των 100 γραμμαρίων, στη δεύτερη στήλη το νέο μήκος του ελατηρίου 23 cm και στην τρίτη στήλη καταγράφουν το «πόσο αυξήθηκε το μήκος», την τιμή δηλαδή 1 cm. Επαναλαμβάνουν με βαρίδι διπλάσιου βάρους και στη συνέχεια με βαρίδι τριπλάσιου βάρους καταγράφοντας τις αντίστοιχες τιμές.

Τα πρώτα συμπεράσματα . Η αύξηση του μήκους του ελατηρίου είναι ανάλογη προς το βάρος του σώματος που κρεμάσαμε. Εφόσον το βάρος θεωρείται «δύναμη» μπορούμε να ισχυριστούμε ότι

Η αύξηση του μήκους του ελατηρίου είναι ανάλογη προς τη δύναμη που ασκείται στο σώμα που κρεμάσαμε.

Ο διδάσκων ενημερώνει τους μαθητές του ότι όλες οι μετρήσεις που έχουν γίνει δείχνουν αυτό που συνέβη και με το πείραμα συμβαίνει με όλα τα ελατήρια, οποιοδήποτε βαρίδι και να κρεμάσουμε. Δηλαδή ότι η αύξηση του μήκους κάθε ελατηρίου είναι ανάλογη προς τη δύναμη που ασκείται στο σώμα που κρεμάσαμε.

Τον 17^ο αιώνα ο Άγγλος ερευνητής Ρόμπερτ Χουκ διατύπωσε, έναν από τους πρώτους νόμους της Φυσικής, τον νόμο για παραμορφώσεις, σαν αυτές που συμβαίνουν σε ένα ελατήριο.

«Η παραμόρφωση ενός ελατηρίου είναι ανάλογη προς τη δύναμη που την προκαλεί».

http://digitalschool.minedu.gov.gr/modules/document/file.php/DSGYM-B200/ExperimentsBGYM/bG/bG.html . Ηλίας Σιτσανλής. Νόμος του Hooke.

Ο νόμος ισχύει τόσο για ελατήριο τεντωμένο οπότε «τραβά» το σώμα που βρίσκεται στο άκρο του και η παραμόρφωση είναι «αύξηση του μήκους» ,

όσο και για ελατήριο που έχει συσπειρωθεί οπότε «σπρώχνει» το αντικείμενο στο άκρο του και η παραμόρφωση είναι «ελάττωση του μήκους»

Δυναμόμετρο. Με βάση τα παραπάνω οι φυσικοί έφτιαξαν ένα όργανο με το οποίο μπορούμε να μετράμε την τιμή μιας δύναμης. Το όνομά του είναι δυναμόμετρο. Η μονάδα μέτρησης της δύναμης στη φυσική είναι το «ένα νιούτον». Συμβολίζεται με 1 Ν. Ένα νιούτον είναι όσο περίπου το βάρος ενός αντικειμένου 100 γραμμαρίων. Τα περισσότερα δυναμόμετρα είναι βαθμολογημένα σε νιούτον. Με το δυναμόμετρο μπορούμε να μετράμε και το βάρος ενός σώματος.

Ο εργαστηριακός ζυγός λειτουργεί με βάση τη δύναμη που ασκείται σε αυτόν. Αν σπρώξουμε – πιέσουμε την πλατφόρμα του ζυγού με το χέρι, ο ζυγός κάτι θα δείξει. Με τον ζυγό, ωστόσο, μπορούμε να μετρήσουμε και το βάρος αλλά και τη μάζα. Οι περισσότεροι από τους ζυγούς του εργαστηρίου είναι βαθμολογημένοι σε μονάδες μάζας. Δείχνουν τη μάζα του σώματος, συνήθως σε γραμμάρια.

Υλικό για αξιολόγηση

1. Συμφωνίες και διαφωνίες.

Με ποια από τα παρακάτω συμφωνείτε ; Με ποια διαφωνείτε;

α. Η «αντίσταση- δυσφορία» την οποία εκδηλώνει ένα σώμα στη μετακίνησή του περιγράφεται με την έννοια όγκος.

β. Ένα σώμα Α έχει μάζα 3πλάσια από ένα άλλο Β. Το βάρος του Α είναι 9πλάσιο από το βάρος του Β.

γ. Ένα σώμα Α έχει μάζα 4πλάσια από ένα άλλο Β. Το βάρος του Α είναι 4πλάσιο από το βάρος του Β.

δ. Αν ένα χάλκινο αντικείμενο ένα ζεστό πρωινό του Ιουλίου έχει μάζα 200 g, η μάζα του μια κρύα νύχτα του χειμώνα θα είναι λίγο μικρότερη

ε. Ο αέρας της σχολικής αίθουσας έχει μάζα αλλά δεν έχει βάρος.

2. Το αυτοκίνητο.

Ένα αυτοκίνητο έχει κατασκευαστεί από 770 κιλά χάλυβα, 180 κιλά σίδηρο, 110 κιλά πλαστικό, 80 κιλά αλουμίνιο και 60 κιλά ελαστικών. Υπάρχουν και ορισμένα ακόμα μέταλλα αλλά σε πολύ μικρές αναλογίες και η συμμετοχή τους στη διαμόρφωση του βάρους μπορεί να αγνοηθεί. Πόση είναι περίπου η μάζα του αυτοκινήτου; Πόση θα είναι αν ζεσταθεί το αυτοκίνητο ;

3. Από αλουμίνιο

Ένα κομμάτι αλουμίνιο και ένας μαθητής. Με το ζυγό βρήκε ότι η μάζα του είναι 81 g. Με τον ογκομετρικό σωλήνα μέτρησε τον όγκο του και τον βρήκε ίσο με 30 cm³ ( 30 μιλιλίτρ).. Σας ζητούμε να υπολογίσετε «πόσα γραμμάρια αντιστοιχούν σε κάθε κυβικό εκατοστό».

Ένα κομμάτι αλουμίνιο πιο ογκώδες από το προηγούμενο. Το ζύγισε και βρήκε ότι η μάζα του είναι 135 γραμμάρια. Με τον ογκομετρικό σωλήνα βρήκε ότι ο όγκος του είναι 50 cm³. Σας ζητούμε να υπολογίσετε «πόσα γραμμάρια αντιστοιχούν σε κάθε κυβικό εκατοστό» γι αυτό το αντικείμενο.

Ένα μικρό κομμάτι αλουμίνιο. Το ζύγισε και βρήκε ότι η μάζα του είναι 27 γραμμάρια. Με τον ογκομετρικό σωλήνα βρήκε ότι ο όγκος του είναι 10 cm³. Σας ζητούμε να υπολογίσετε «πόσα γραμμάρια αντιστοιχούν σε κάθε κυβικό εκατοστό» γι αυτό το αντικείμενο.

Σας ζητούμε τέλος να συγκρίνετε τα αποτελέσματα να βγάλετε κάποιο συμπέρασμα.

4. Χάλκινα αντικείμενα

Δύο χάλκινα αντικείμενα με διαφορετικό σχήμα . Ζυγίζουμε το μικρότερο και βρίσκουμε 89 g, κάνουμε ογκομέτρηση και βρίσκουμε 10 cm³ ( 10 μιλιλίτρ). Σας ζητούμε να υπολογίσετε «πόσα γραμμάρια αντιστοιχούν σε κάθε κυβικό εκατοστό»΄. Στη συνέχεια ζυγίζουμε το μεγαλύτερο και βρίσκουμε 267 g, κάνουμε ογκομέτρηση και βρίσκουμε 30 cm³ ( 30 μιλιλίτρ). Σας ζητούμε να υπολογίσετε «πόσα γραμμάρια αντιστοιχούν σε κάθε κυβικό εκατοστό» γι αυτό το αντικείμενο.

Σας ζητούμε να συγκρίνετε τα δύο αποτελέσματα να βγάλετε κάποιο συμπέρασμα.

Μπορείτε να προβλέψετε πόσο θα ζυγίζει ένα χάλκινο αντικείμενο όγκου 50 cm³ ;

5. Η μάζα ενός «φαντάσματος»

Ο αόρατος αέρας μέσα στην σχολική αίθουσα.

α. Δεν είναι δυνατόν να έχει μάζα

β. Η μάζα του είναι γύρω στα 10 g.

γ. Η μάζα του είναι γύρω στα 2 kg δύο κιλά.

δ. Η μάζα του είναι πάνω από 100 kgΓ.

ε. Δεν είναι δυνατόν να έχει βάρος

στ. Το βάρος του είναι μεγαλύτερο από το βάρος ενός συνηθισμένου ανθρώπου

Με ποια από τα παραπάνω συμφωνείτε ;

6. Να μετρήσουμε και να βγάλουμε συμπεράσματα

Σας ζητούμε να μετρήσετε με υποδεκάμετρο το μήκος του ελατηρίου του σχήματος σε κάθε μία από τις περιπτώσεις της επιμήκυνσής του, να υπολογίσετε κάθε φορά τη διαφορά του μήκους από το «αρχικό μήκος» - στην εικόνα αριστερά – και να καταγράψετε το συμπέρασμά σας.

7. Τα διαφορετικά βαρίδια και το υποδεκάμετρο. .

Ένα ελατήριο έχει μήκος 21 cm. Διατηρώντας το κατακόρυφο, ένας μαθητής κρεμά στο άκρο του δύο βαρίδια το ένα 100 g και το άλλο 50 g, μετρά με υποδεκάμετρο το μήκος του τεντωμένου ελατηρίου και το βρίσκει 24 cm.

α. Πόσο επιμηκύνθηκε το ελατήριο ;

Ο μαθητής αντικαθιστά το βαρίδι των 50 g με ένα άλλο των 200 g και αφήνοντας το «100 g» στη θέση του. Με το υποδεκάμετρο διαπιστώνει ότι το μήκος του ελατηρίου γίνεται 27 cm.

β. Πόση είναι τώρα η επιμήκυνση ; γ. Βγάζετε κάποιο συμπέρασμα ;

8. Η Αλίκη και το δυναμόμετρο.

Η Αλίκη κρατά στο ένα χέρι το δυναμόμετρο, ζυγίζει ένα μικρό αντικείμενο και βρίσκει 3,5 Ν.

Τι πρέπει να κάνει - με άλλο χέρι- στο αντικείμενο ώστε η ένδειξη να είναι 2 Ν;

Να το σπρώξει προς τα πάνω, έτσι ώστε η δύναμη που θα ασκεί να είναι 1,5 Ν ;

Να το τραβήξει προς τα κάτω έτσι ώστε η δύναμη που θα ασκεί να είναι 1,5 Ν ;

Παραπομπές

1. Ο άνεμος πρέπει να είναι ένας συνηθισμένος άνεμος, γιατί υπάρχουν βέβαια και άνεμοι που παίρνουν ακόμα και ανθρώπους και όχι μόνο.

2. Η διδασκαλία της έννοιας μάζα στη Δευτεροβάθμια εκπαίδευση – και όχι μόνο στην ελληνική - περιβάλλεται από αξιοσημείωτη σύγχυση, σε κάποιο βαθμό δικαιολογημένη. Η σύγχυση χρονολογείται από τη δημοσίευση των Principia του Νewton και οφείλεται στους τρεις εννοιολογικούς μανδύες με τους οποίους ενδύεται η λέξη μάζα στο πλαίσιο της κλασικής φυσικής: στον ορισμό Ι των Principia η μάζα ορίζεται ως «ποσότητα της ύλης», στο δεύτερο νόμο της κίνησης εμφανίζεται ως «μέτρο της αδράνειας», ενώ στο νόμο της παγκόσμιας έλξης ως υπεύθυνη για την αμοιβαία βαρυτική έλξη μεταξύ των σωμάτων. Προηγουμένως, μέσα από περιγραφές διαδοχικών πειραμάτων, τα οποία ισχυρίζεται ότι πραγματοποίησε ο ίδιος, ο Newton προσπαθεί επίμονα ( Philosophiae Naturalis Principia Mathematica στην αγγλική μετάφραση του Andrew Motte αναθεωρημένη από τον Florian Cajori, Book I, experiments by pendulums) να αναδείξει την αναλογία της προς το βάρος. Η επιμονή του οφείλεται στο ότι εκτιμά ότι ο πιο «βολικός» τρόπος για τη μέτρησή της αυτός με τον ζυγό.

Κατά τη διδασκαλία μας η αναφορά στην αναλογία μάζας και βάρους και η χρήση για τη μέτρηση του ζυγού έχει σοβαρότατο μειονέκτημα. Επιτείνει την εννοιακή σύγχυση των διδασκομένων ότι η μάζα και το βάρος είναι κάτι παρόμοιο, όπως έχει καταδειχθεί από σχετικές έρευνες σε διάφορα εκπαιδευτικά συστήματα. Και όσο δεν επιμένουμε στην αδρανειακή πτυχή της έννοιας – η οποία είναι και η βασική – θα πληρώνουμε το σχετικό «τίμημα».

Ωστόσο για τη διδασκαλία στην Α΄ Γυμνασίου το πιο αποτελεσματικό είναι η μέτρηση να γίνεται με ζυγό, όπως εξάλλου κάνουν και οι χημικοί σε κάθε περίπτωση για τη μέτρησή της. χωρίς να μας διαφεύγει ότι

α. Ο βασικός στόχος της διδασκαλίας στην Α΄ Γυμνασίου οφείλει να είναι η ΕΞΟΙΚΕΙΩΣΗ των διδασκομένων με τις τρεις πτυχές της έννοιας

β. Η μύηση στην έννοια μάζα θα συνεχιστεί και κατά τα επόμενα με σκοπό να εμπλουτίζεται .

3. Επειδή ο όγκος του νερού αλλοιώνεται με τη θερμοκρασία η συμφωνία πρόβλεπε ότι ένα kg είναι η μάζα νερού ενός λίτρου σε θερμοκρασία 4 βαθμών Κελσίου.

4. Η έννοια ΟΓΚΟΣ ως πανάρχαια έννοια της Γεωμετρίας αναφέρεται σε ΓΕΩΜΕΤΡΙΚΟ ΣΤΕΡΕΟ, είναι ο όγκος κάποιου όχι υλικού «γεωμετρικού στερεού».Πολύ πριν από την εμφάνιση την εμφάνιση της Φυσικής η Τεχνολογία είχε χρησιμοποιήσει την έννοια «όγκος ενός σώματος» και διέθετε και μονάδες μέτρησης. Για τη Φυσική η συνώνυμη έννοια αναφέρεται σε ΥΛΙΚΟ ΣΩΜΑ. Είναι «ΟΓΚΟΣ ΤΟΥ ΣΩΜΑΤΟΣ» και συνιστά πρωταρχική ιδιότητα κάθε υλικού σώματος. Για τον Isaac Newton ( Principia ) ένα σώμα θεωρείται υλικό σώμα εφόσον «διαθέτει» ΟΓΚΟ και ΑΔΡΑΝΕΙΑ. Για να προσδιορίσει ωστόσο την ποσότητα της ύλης – τη θεωρούμενη ως μάζα - καταφεύγει στην ιδιότητα «αδράνεια». Η «ποσότητα όγκου» ενός υλικού σώματος είναι ίση με τον όγκο του αντίστοιχου – μη υλικού – γεωμετρικού στερεού της Γεωμετρίας .

5.Ο πίνακας με την κουρτίνα είναι έργο του Anrdrew Wyeth, ενός από τους μεγαλύτερους Αμερικανούς ζωγράφους του 20^ου αιώνα

6. Η θεωρία ότι σε φαινόμενα θέρμανσης και ψύξης η τιμή της μάζας ενός σώματος επηρεάζει την αλλαγή της θερμοκρασίας συνιστά γνωστικό αντικείμενο που θα διδαχθεί σε άλλη φάση.

Ανδρέας Ιωάννου Κασσέτας