Ανδρέας Ιωάννου Κασσέτας

Η έννοια ΡΟΠΗ ΑΔΡΑΝΕΙΑΣ

Εμπειρία σώματος . Τότε. Ήταν παιδί και χρειάστηκε να μετακινηθεί πάνω σε ένα πολύ στενό οριζόντιο «γεφύρωμα» σε κάποιο ύψος πάνω από το έδαφος. Διαισθάνθηκε τον κίνδυνο να ανατραπεί και ενστικτωδώς τέντωσε και τα δύο του χέρια ώστε να γίνουν οριζόντια . Για κάποιο λόγο το σώμα του με τα τεντωμένα χέρια παρουσίασε μεγαλύτερη «αντίσταση» στο να του συμβεί η ανατροπή, στο να συμβεί η περιστροφή που θα είχε σαν συνέπεια να πέσει. Με το τέντωμα των χεριών κάτι άλλαξε , όχι βέβαια η μάζα του και ο κίνδυνος περιορίστηκε. Κάτι άλλαξε και αυξήθηκε η «δυσφορία» του σώματός του στο να στραφεί και αυτό που άλλαξε δεν ήταν η μάζα του.

Ο Newton και η στροφική κίνηση. Ο Euler

Αυτό που κάνω στο μάθημά μου δεν είναι ιστορία της κβαντομηχανικής αλλά μια

παιδαγωγική ανακατασκευή αυτής της ιστορίας ..

Πρόκειται δηλαδή για ένα είδος έλλογης επανακάλυψης.

Στέφανος Τραχανάς, Το φάντασμα της Όπερας

Τέλη του 17^ου αιώνα και η απόπειρα των στοχαστών για μια – επί τέλους – περιγραφή του φαινομένου κίνηση έχει για τα καλά πυροδοτηθεί. Ο Άγγλος πατριάρχης της απόπειρας με βάση τη μελέτη του particulus και με εργαλείο τις έννοιες πρωταγωνίστριες μάζα, δύναμη και ορμή έχει καταλήξει σε νόμους της κίνησης με βασικό στόχο τη λειτουργία του ηλιακού συστήματος .Τα επίγεια ωστόσο αντικείμενα –- ανεμόμυλοι, φύλλα δέντρων, ανθρώπινα εκτελούσαν κινήσεις «απερίγραπτες» και η ιδέα ότι μέσα στην κίνηση κάθε πανάρχαιου «τροχού» εμπεριέχεται μια περιστροφή είχε ήδη κάνει την εμφάνισή της. Ωστόσο στο Principia του Newton το φαινόμενο «στροφική κίνηση στερεού» παρουσιάζεται μόνο στον πρώτο νόμο της κίνησης - νόμο της αδράνειας. Ο «πατριάρχης» υποστηρίζει ότι ένα στρεφόμενο στερεό, όπως ο πλανήτης Γη, δεν σταματά να στρέφεται – υπονοώντας ότι η κίνηση του θα γίνεται με σταθερό ρυθμό – εφόσον δεν ασκούνται σε αυτό δράσεις.

Εμπειρικά στοιχεία από εκκρεμή, τροχούς, σβούρες και νερόμυλους είχαν συσσωρευτεί αλλά απουσίαζαν οι ΕΝΝΟΙΕΣ.

Ροπή της μάζας – αδράνειας. Ο Λέοναρντ Όιλερ

Η γενικότερη περιγραφή και ερμηνεία του φαινομένου «στροφική κίνηση στερεού» απαιτούσε καινούριες έννοιες οι οποίες στα χρόνια που ακολούθησαν την έκδοση του Principia έκαναν τελικά την εμφάνισή τους αρχικά ως πλάσματα της Σκέψης των Ευρωπαίων ερευνητών. Με δεδομένο ότι οι τρεις έννοιες που θεμελίωσαν τη νευτωνική δυναμική του particulus ήταν η μάζα, η δύναμη και η ορμή, οι δύο από τις τρεις νέες έννοιες ήταν

α. Η αντίστοιχη προς τη δύναμη, « ροπή δύναμης ως προς σημείο» . Προτάθηκε από τον Γάλλο Pierre Varignon , Πιερ Βαρινιόν, - θα μπορούσαμε να πούμε σαν το «αντίστοιχο της δύναμης» προκειμένου για τη θεωρητική μελέτη του φαινομένου

ισορροπία ( Mechanique Nouvelle au Statique, - Νέα Μηχανική ή Στατική - εκδόθηκε το 1725) και

β. Η αντίστοιχη προς τη ορμή. Μια δεκαετία μετά τον θάνατο του «πατριάρχη» και ο τριαντάχρονος τότε γεννημένος στη Βασιλεία της Ελβετίας, Leonhard Euler, Λέοναρντ Όιλερ – ο οποίος θα αξιοποιούσε όσο κανείς στο παρελθόν τον διαφορικό λογισμό στην οικοδόμηση της Μηχανικής - αφού άδραξε τη ροπή δύναμης για να την χρησιμοποιήσει και στη στροφική κίνηση – και όχι μόνο στο φαινόμενο ισορροπία – πρότεινε και τη ροπή της ορμής – τη λεγόμενη και στροφορμή ορίζοντάς την με τρόπο παρόμοιο με εκείνον που είχε οικοδομήσει τη ροπή της δύναμης ως προς σημείο.

Ήταν πρόδηλο ότι για προχωρήσει η μελέτη της στροφικής κίνησης έλειπε η έννοια η αντίστοιχη προς τη μάζα

γ. Η αντίστοιχη προς τη μάζα. Ροπή της μάζας

Δεκαετία του 1730 και ο Euler – Όιλερ – προκειμένου να «πλάσει» την καινούρια έννοια διεύρυνε το αρχικό σημαινόμενο της έννοιας «ροπή».

Στο αρχικό της σημαινόμενο η ροπή ενός μεγέθους ( όπως η δύναμη ή και η ορμή ) ως προς κάποιο σημείο, ήταν μία συνάρτηση στην οποία συνυπήρχαν το μέγεθος (η δύναμη ή η ορμή ) και η απόσταση από το σημείο . Η ροπή δύναμης ως προς σημείο ήταν εξωτερικό γινόμενο «θέση επί δύναμη», η ροπή της ορμής ( στροφορμή) ήταν το εξωτερικό γινόμενο «θέση επί ορμή» .

Ο Όιλερ πρότεινε μία «διαφορετική ροπή» η οποία δεν ήταν «ροπή διανύσματος» ήταν μια νέα βαθμωτή θετική ποσότητα η οποία αναφερόταν σε υλικό σημείο και σε άξονα, ήταν η ροπή της μάζας-αδράνειας του υλικού σημείου ως προς τον άξονα. ως γινόμενο της μάζας του υλικού σημείου επί το τετράγωνο της απόστασής του από τον άξονα. Ι = mr² . Για κάθε corpus rigidus – είτε κινούμενο είτε ακίνητο - το άθροισμα των ροπών αδράνειας των υλικών σημείων του, ως προς τον ίδιο άξονα, το θεώρησε ως ροπή της μάζας – αδράνειας του σώματος ως προς τον άξονα.

Στην πρόταση αυτή οδηγήθηκε εφαρμόζοντας τον δεύτερο νευτωνικό νόμο της κίνησης για το σύνολο των υλικών σημείων ενός corpus rigidus σε στροφική κίνηση, διέκρινε ότι η βαθμωτή θετική ποσότητα έκανε την εμφάνισή της, παίζοντας, στην περίπτωση της στροφικής κίνησης, τον ρόλο που έπαιζε η μάζα στο έργο του «Άγγλου δάσκαλου». Ενώ δηλαδή προκειμένου για υλικό σημείο η μάζα του και μόνον αυτή ήταν «μέτρο της δυσφορίας στις αλλαγές» - μέτρο της αδράνειας- προκειμένου για στρεφόμενο σώμα το μέτρο της «δυσφορίας στις αλλαγές» ήταν η ροπή της μάζας-αδράνειας.

Στα μέσα του 18^ου αιώνα, με την παρέμβαση του Όιλερ, έχουν εδραιωθεί τρεις «εκδοχές ροπής».

Η ροπή δύναμης, αντίστοιχη με την έννοια δύναμη,

η ροπή της ορμής, αντίστοιχη με την έννοια ορμή και

η ροπή της μάζας-αδράνειας αντίστοιχη με την έννοια μάζα.

Ροπή της μάζας- αδράνειας .

Σε όλες τις ευρωπαϊκές γλώσσες¹ η νέα έννοια θεωρείται «ροπή» κάποιας άλλης φυσικής ποσότητας, η οποία εν προκειμένω είναι η - με μοναδικό μέτρο τη μάζα – αδράνεια.

Στις περισσότερες των περιπτώσεων ο όρος συγκροτείται από δύο λέξεις, η μία με σημαινόμενο τη γενικότερη έννοια «ροπή», η άλλη με σημαινόμενο τη φυσική ποσότητα αδράνεια-μάζα.

Συνήθως οι δύο λέξεις γίνονται τρεις διότι συνδέονται και με άρθρο δηλωτικό της γενικής πτώσης,

Στα αγγλικά η ροπή είναι moment, η αδράνεια inertia και η ροπή αδράνειας moment of inertia,

στα γαλλικά η ροπή moment, η αδράνεια inertie και η ροπή αδράνειας moment d'inertie,

H έννοια «ροπή αδράνειας ως προς άξονα» εισάγεται από τον Euler με βάση τρεις παραδοχές

α. ότι η έννοια αναφέρεται σε οποιοδήποτε αντικείμενο με αδράνεια– μάζα, ΑΝΕΞΑΡΤΗΤΑ από το εάν κινείται ή δεν κινείται αλλά και από το «πώς κινείται».

β. ότι ένα corpus rigidus ( άκαμπτο στερεό σώμα ) είναι ένα πεπερασμένο ΣΥΝΟΛΟ υλικών σημείων με αναλλοίωτες τις μεταξύ τους αποστάσεις

γ. ότι η -ως προς κάποιον οποιονδήποτε άξονα- ροπή αδράνειας ενός υλικού σημείου μάζας m ορίζεται ως ίση με την ποσότητα mx², όπου x η στιγμιαία γεωμετρική απόσταση του γεωμετρικού σημείου στο οποίο βρίσκεται το υλικό σημείο από τον άξονα.. Θεωρεί τη ροπή αδράνεια ενός σώματος ως άθροισμα των ροπών αδράνειας των υλικών σημείων τα οποία το συγκροτούν. Ι= Σmx² .

Η τιμή της ροπής αδράνειας

Η τιμή της ροπής αδράνειας ενός σώματος ως προς κάποιο άξονα εξαρτάται από τη μάζα του σώματος αλλά και από το ‘πώς κατανέμεται το υλικό του σώματος ως σε σχέση με τον άξονα . Όταν μια κοπέλα τεντώνει τα χέρια της, η μάζα της διατηρείται αναλλοίωτη αλλά η ροπή αδράνειας του σώματός της, ως προς κατακόρυφο άξονα διερχόμενο από το κέντρο μάζας αυξάνεται.

Καθώς ο Φρειδερίκος ο Μέγας λύγιζε τα χέρια, ανοίγοντάς τα προς τα έξω η ροπή αδράνειας του σώματός του ως προς κατακόρυφο άξονα διερχόμενο από το κέντρο μάζας παρουσίαζε αύξηση

Η φυσική σημασία της έννοιας.

Το «παράξενο» αυτό άθροισμα προέκυψε όταν θέλησε να επεκτείνει τον αναφερόμενο σε particulus - υλικό σημείο - δεύτερο νευτωνικό νόμο της κίνησης στη στροφική κίνηση του corpus rigidus. Αξιοποιώντας τις έννοιες «ροπή δύναμης» ( σύμβολο τ ) και γωνιακή επιτάχυνση στρεφόμενου στερεού ( σύμβολο α_γων ) απέδειξε ότι η αντίστοιχη προς την F = ma εξίσωση

για στρεφόμενο στερεό είναι η τ = (Σmx²) α_γων .

Στη εξίσωση που προκύπτει ( λέγεται και 2^ος νόμος του Euler)

α. η έννοια «ολική ροπή» κατά τον άξονα περιστροφής ( η συνιστώσα της ροπής κατά τη διεύθυνση του άξονα ) παίζει τον ρόλο που παίζει η έννοια δύναμη στην κίνηση κάθε υλικού σημείου ενώ

β. η ποσότητα (Σmx²) –ορίζεται ως ροπή αδράνειας ως προς σταθερό άξονα που συμπίπτει με τον άξονα της περιστροφής και συμβολίζεται με το Ι ( αρχικό του lnertia) – παίζει τον ρόλο που παίζει η μάζα – μέτρο της αδράνειας/δυσφορίας στις αλλαγές - στην κίνηση του υλικού σημείου.

Υπό την έννοια αυτή ως φυσική σημασία της έννοιας ροπή αδράνειας μπορεί να θεωρηθεί «η αδράνεια – δυσφορία» που εκδηλώνει το στερεό κατά τις μεταβολές της στροφικής του κίνησης.

Με άλλα λόγια η γωνιακή επιτάχυνση ενός στερεού ( η οποία περιγράφει τον ρυθμό μεταβολής της γωνιακής ταχύτητας) καθορίζεται από δύο συγκεκριμένους παράγοντες

α. Από την ολική ροπή - κατά τον άξονα περιστροφής - των ασκουμένων στο σώμα δυνάμεων. Η ολική αυτή ροπή θα συμβάλει στη διαμόρφωση της τιμής και της κατεύθυνσης της γωνιακής ταχύτητας και

β. από τη ροπή αδράνειας του σώματος ως προς άξονα που συμπίπτει με τον άξονα της περιστροφής η οποία θα συμβάλει στο να διαμορφωθεί η τιμή της γωνιακής επιτάχυνσης.

Όπως η εξίσωση F = ma ισχύει για υλικό σημείο σταθερής μάζας , αντίστοιχα η εξίσωση τ = Iα_γων . ισχύει για στρεφόμενο στερεό σταθερής ροπής αδράνειας.

Στη συνέχεια η ροπή αδράνειας θα συμβάλει

α. στη μορφοποίηση μιας σχέσης για τη στροφορμή ενός στρεφόμενου στερεού.

Στην περίπτωση αυτή από την τιμή της στροφορμής ενός υλικού σημείου ως προς κάποιο γεωμετρικό σημείο ( εξωτερικό γινόμενο της θέσης, ως προς την αρχή των αξόνων ενός συστήματος αναφοράς επί την ορμή του υλικού σημείου ως προς αυτό το σύστημα αναφοράς ) οδηγείται κανείς στον υπολογισμό της στροφορμής του, με γωνιακή ταχύτητα ω , στρεφόμενου στερεού, θεωρώντας το ως σύνολο υλικών σημείων και βασιζόμενος στον ορισμό της έννοιας «στροφορμή ενός συστήματος υλικών σημείων» .

Η κατάληξη είναι L = ω(Σmx²) ή L = Ιω

β. στη μορφοποίηση μιας σχέσης για την κινητική ενέργεια του στρεφόμενου στερεού. Από την τιμή της κινητικής ενέργειας ενός υλικού σημείου μάζας m και ταχύτητας υ (½ mυ²) οδηγείται κανείς στον υπολογισμό της κινητικής ενέργειας Κ του με γωνιακή ταχύτητα ω , στρεφόμενου σώματος, θεωρώντας το ως σύνολο υλικών σημείων και βασιζόμενος στον ορισμό της έννοιας «στροφορμή ενός συστήματος υλικών σημείων» . Η κατάληξη είναι Κ = ½ω²(Σmx²) ή Κ = ½ Ιω² .

Σε περίπτωση που η ροπή αδράνειας του σώματος δεν είναι σταθερή η εξίσωση για τη στροφική κίνηση τ = Iα_γων δεν μπορεί να ανταποκριθεί στην ερμηνεία και την πρόβλεψη των γεγονότων. Ο Euler για τη γενικότερη αυτή περίπτωση παρουσίασε το 1754, ως γενικότερο νόμο ( αναφέρεται και ως 2^ος νόμος του Euler ) για τη στροφική κίνηση τον διατυπωμένο με την εξίσωση τ = dL/dt στην οποία η ολική ροπή είναι ίση με τον ρυθμό μεταβολής της στροφορμής. Στην εξίσωση αυτή το τ συμβολίζει τη συνιστώσα της ολικής ροπής κατά τον άξονα περιστροφής ( τη λεγόμενη «ολική ροπή κατά τον άξονα) ενώ το L τη συνιστώσα της στροφορμής κατά τον άξονα περιστροφής.

Όσο για την έννοια «ροπή αδράνειας υλικού σημείου» αυτή εκφράζει τη “συμβολή του υλικού σημείου» στην εκδήλωση δυσφορίας του σώματος σε περίπτωση που επίκειται μεταβολή της στροφικής κινητική του κατάστασης.

Ο ίδιος ο Euler αργότερα θεωρεί και μια συνεχή κατανομή μάζας σε ομογενή στερεά με ειδικό γεωμετρικό σχήμα και εφαρμόζει διαφορικό λογισμό προκειμένου να υπολογίσει τη τιμή της με ολοκλήρωμα.

Με την πραγματεία του Mechanica, o Όιλερ έκανε στη Μηχανική ότι έκανε ο Descartes στη Γεωμετρία. Την απελευθέρωσε από τα δεσμά της συνθετικής παρουσίασης, την έκανε αναλυτική. Το Principia του Newton θα μπορούσε να είχε γραφτεί από τον Αρχιμήδη. Το Mechanica του Euler δεν θα μπορούσε να έχει γραφτεί από κανέναν Έλληνα. Για πρώτη φορά ολόκληρη η ισχύς του Calculus κατευθύνθηκε στη Μηχανική, σηματοδοτώντας το πέρασμα της βασικής επιστήμης στη σύγχρονη εποχή.

Το θεώρημα των παραλλήλων αξόνων

Γεννημένος, όπως και ο Όιλερ, στην Ελβετία, αλλά πολλά χρόνια μετά, το 1796,

ο γερμανόφωνος Jacob Steiner εξελίχτηκε σε έναν από τους σημαντικότερους μαθηματικούς της γενιάς του. Το 1830, εστιάζοντας στη Μηχανική του στερεού και ειδικά στις έννοιες ροπή αδράνειας και κέντρο μάζας οδηγήθηκε στο λεγόμενο θεώρημα των παραλλήλων αξόνων το οποίο συνιστά μία από τις σημαντικές προσφορές των ευρωπαίων μαθηματικών στην οικοδόμηση της Μηχανικής του στερεού rigid body.

Αναφέρεται και ως «θεώρημα του Στάινερ, σε γλώσσα γερμανική der Steinersche Satz. Οι αγγλόφωνοι το αναφέρουν και ως Steiner's parallel-axis theorem.

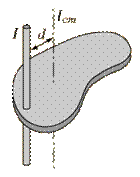Το Θεώρημα συσχετίζει τη ροπή αδράνειας ενός σώματος ως προς κάποιο άξονα με τη ροπή αδράνειας του ίδιου σώματος ως προς τον άξονα τον παράλληλο με τον x αλλά διερχόμενο από το κέντρο μάζας I = I_cm + md² .

Με αυτό, αποδεικνύεται, εκτός των άλλων, και ότι η ροπή αδράνειας ενός σώματος ως προς άξονα Α_cm διερχόμενο από το κέντρο μάζας έχει τη μικρότερη από όλες τις τιμές των ροπών αδράνειας που παρουσιάζει το σώμα ως προς οποιονδήποτε άλλο άξονα παράλληλο προς τον Α _cm.

Η έννοια ΡΟΠΗ ΑΔΡΑΝΕΙΑΣ και η διδασκαλία μας

1. Διδακτικοί στόχοι

α. Να είναι οι μαθητές σε θέση να απαντήσουν στα απαντούν στα ερωτήματα «τι λέγεται ροπή αδράνειας»

«σε τι αναφέρεται» και «ποια είναι η φυσική της σημασία».

β. Να εξοικειωθούν οι μαθητές με τη μέθοδο που χρησιμοποιεί η Φυσική

σύμφωνα με την οποία βασίζεται ισόρροπα

από τη μια σε μια θεωρητική πρακτική με μαθηματικές επεξεργασίες

και από την άλλη σε μια εργαστηριακή πρακτική κατά την οποία επιλέγεται ένα συγκεκριμένο φαινόμενο, γίνονται κατάλληλες μετρήσεις

και εξακριβώνεται κατά πόσο τα συμπεράσματα της μια πρακτικής συγκλίνουν με τα αντίστοιχα της άλλης

γ. Να μπορούν οι μαθητές να απαντούν στα ερωτήματα για τον ρόλο της ροπής αδράνειας στη διατύπωση του νόμου για τη στροφική κίνηση καθώς και για «πώς συμβάλλει» στη διαμόρφωση των σχέσεων

i . για την τιμή της κινητικής ενέργειας και ii . για την τιμή της στροφορμής στρεφόμενου σώματος

2. Διδάσκοντας

Θέτουμε το ζήτημα με τη μορφή ερώτησης

Στη νευτωνική Μηχανική η έννοια ‘’δύναμη’’ εισάγεται ως αιτία μεταβολής της κινητικής κατάστασης. Προκειμένου για υλικό σημείο η μεταβολή της κινητικής κατάστασης περιγράφεται με την έννοια ‘’επιτάχυνση’’ και η σχέση ανάμεσα στην «αιτία» (δύναμη) και στο «αποτέλεσμα» επιτάχυνση εκφράζεται με τον δεύτερο νόμο της κίνησης (θεμελιώδη νόμο της Μηχανικής) μέσα από την εξίσωση F= mα. Στον θεμελιώδη αυτό νόμο έναν ιδιαίτερο ρόλο παίζει η - συμβολιζόμενη με m - μάζα (αδράνειας). Αποτελεί μέτρο της αδράνειας («δυσφορίας», αντίστασης) την οποία εκδηλώνει το σώμα κατά τη μεταβολή της κινητικής του κατάστασης. Αυτά όμως ισχύουν για υλικό σημείο σε οποιαδήποτε κίνηση.

α. Τι συμβαίνει για ένα στερεό σώμα σε μεταφορική κίνηση;

β. Τι συμβαίνει για ένα στερεό σώμα σε στροφική κίνηση;

Δημιουργούμε το κατάλληλο κλίμα ώστε να παρουσιάσουμε τις απαντήσεις

. Στην περίπτωση της μεταφορικής κίνησης ισχύει ότι και για την κίνηση του υλικού σημείου δεδομένου ότι το κέντρο μάζας εκτελεί κίνηση με ορισμένη επιτάχυνση

. Στην περίπτωση του στρεφομένου στερεού η αντίστοιχη με την ταχύτητα έννοια με την οποία περιγράφεται η κινητική κατάσταση είναι η γωνιακή ταχύτητα και η αντίστοιχη προς την επιτάχυνση έννοια είναι η γωνιακή επιτάχυνση. Όσο για «αιτία» της μεταβολής πρέπει να θεωρήσουμε την (ολική) ροπή. Ποια έννοια όμως θα εκφράσει την αδράνεια (δυσφορία) του στρεφόμενου στερεού στις μεταβολές της στροφικής κίνησης; Δεν υπάρχει άλλη λύση από το να θεωρήσουμε το στρεφόμενο στερεό ως «σύνολο υλικών σημείων» τα οποία κινούνται κυκλικά και να εφαρμόσουμε τον δεύτερο θεμελιώδη νόμο σε καθένα από αυτά και να επεξεργαστούμε μαθηματικά το ζήτημα ώστε να εμφανιστεί η ολική ροπή .

Θα προκύψει τ_ολ ( ολική ροπή ) = a_γων Σm_i r_i² .

Καταλήγουμε σε μια σχέση αναλογίας ανάμεσα στην αιτία (ολική ροπή) και στο αποτέλεσμα (γωνιακή επιτάχυνση). Στη θέση της μάζας «διακρίνουμε» την ποσότητα Σm_i r_i². Η ποσότητα αυτή αποτελεί έννοια/μέγεθος η οποία στη μηχανική του στρεφομένου στερεού «παίζει τον ρόλο που παίζει η μάζα αδράνειας στη μηχανική του υλικού σημείου». Λέγεται ροπή αδράνειας του σώματος ως προς άξονα και συμβολίζεται με το κεφαλαίο Ι, αρχικό της λατινικής λέξης Inertia.

Η προκύπτουσα εξίσωση τ_ολ = Ιa_γων μαθηματική έκφραση του δεύτερου νόμου για τη στροφική κίνηση περιγράφει και τη φυσική σημασία της έννοιας ροπή αδράνειας ως αντίσταση – «δυσφορία» του σώματος σε κάθε μεταβολή της γωνιακής ταχύτητας

Αν το σώμα είναι ομογενές και έχει ένα γεωμετρικό σχήμα όπως η σφαίρα η ροπή αδράνειας ως προς ένα άξονα συμμετρίας υπολογίζεται μαθηματικά ίση με 2/5 mR² .

3. Να μετρήσουμε τη ροπή αδράνειας

Ποιο θα είναι το ΦΑΙΝΟΜΕΝΟ ;

Ένα σημαντικό βέβαια ερώτημα είναι το «πώς μπορούμε να τη μετρήσουμε πειραματικά» τη ροπή αδράνειας ενός σώματος με δεδομένο ότι διαθέτουμε μία συνήθη σχολική εργαστηριακή υποδομή

Θα χρειαστεί να επιλέξουμε ένα ΦΑΙΝΟΜΕΝΟ στο οποίο να εκδηλωθεί η «αντίσταση στη μεταβολή της στροφικής κινητικής κατάστασης » .

Ανοίγουμε συζήτηση με όλους τους μαθητές σχετικά με το «ποιο θα είναι το φαινόμενο»

Το φαινόμενο θα μπορούσε να είναι είτε ΣΤΡΟΦΙΚΗ ΚΙΝΗΣΗ είτε ΚΥΛΙΣΗ - η οποία αναλύεται σε μεταφορική και στροφική κίνηση - και η από πρακτική σκοπιά το φαινόμενο ΚΥΛΙΣΗ ( χωρίς ολίσθηση ) είναι προτιμότερο.

Εξάλλου η χωρίς ολίσθηση κύλιση μπορεί να θεωρηθεί και ΣΤΡΟΦΙΚΗ ΚΙΝΗΣΗ περί τον στιγμιαίο άξονα περιστροφής που περνά από το σημείο μηδενική ταχύτητας σημείο επαφής της σφαίρας με το επίπεδο

Επιλέγουμε τελικά το φαινόμενο «κύλιση σε κεκλιμένο επίπεδο» με δεδομένο ότι διαθέτουμε κεκλιμένο επίπεδο, χρονόμετρο ή διάταξη με φωτοπύλες, γωνιόμετρο και μετροταινία και παρουσιάζουμε στον πίνακα τη θεωρητική προσέγγιση του όλου ζητήματος

Η θεωρητική προσέγγιση.

Για την ευθύγραμμη κίνηση του κέντρου μάζας εφαρμόζουμε τον δεύτερο νόμο

mgημφ – Τ = ma_cm

Για τη στροφική περί άξονα που περνά από το κέντρο μάζας ισχύει ΤR = I_cma_γων ,

με a_cm= a_γων.R

Αν είναι x η μετατόπιση του κέντρου μάζας x = ½α_cmt ² και από τη Γεωμετρία του τριγώνου x = h/ημφ

Τελικά προκύπτει I_cm = mR² ( gt²ημφ²/2h - 1 ) . H τιμή δηλαδή της ροπής αδράνειας προκύπτει ίση με την ποσότητα mR²επί τον αριθμό ( gt²ημφ²/2h - 1 ) τον οποίο συμβολίζουμε με λ. I_cm = λmR² ή λ = gt²ημφ²/2h -1

Δεδομένου ότι λ = gt²ημφ²/2h - 1 είναι

2h/gημ²φ = t²/(λ+1) συνάρτηση από την οποία μπορούμε να υπολογίσουμε την τιμή του λ

 Η εργαστηριακή δραστηριότητα

Αν υπάρχει η ανάλογη υποδομή είναι προτιμότερο να ερευνηθεί το ζήτημα από τους μαθητές σε ομάδες

Μοιράζουμε σε κάθε μαθητή ένα φύλλο εργασίας και τους καθοδηγούμε στο να στήσουν τη διάταξη με ΚΕΚΛΙΜΕΝΟ ΕΠΙΠΕΔΟ – με μικρή σχετικά γωνία ώστε να λάβει χώρα κύλιση χωρίς ολίσθηση και να αφήσουν τη συμπαγή σφαίρα να κυλίσει μέχρι τη βάση και να μετρήσουν με το γωνιόμετρο τη γωνία φ, με χρονόμετρο (ή με φωτοπύλες) το χρονικό διάστημα t τον χρόνο και με μετροταινία το ύψος

Τους ζητάμε επίσης να επαναλάβουν δύο ακόμα φορές τις μετρήσεις με διαφορετική γωνία και ύψος,

να καταγράφουν τα αποτελέσματα στο φύλλο εργασίας και να κάνουν τη γραφική παράσταση της συνάρτησης 2h/gημ²φ = t²/(λ+1) y = f(t²) με y = 2h/gημ²φ

Για καθεμία από τις μετρήσεις κάνουμε πίνακα τιμών

από τη μια η ποσότητα 2h/gημ²φ

και από την άλλη οι τιμές t² του αντίστοιχου χρονικού διαστήματος στο τετράγωνο.

Από την κλίση υπολογίζουμε την τιμή λ+1 άρα και το λ.

Για τη σφαίρα προκύπτει περίπου 0,4 - αλλά όχι ακριβώς 0,4 - και συζητάμε με τους μαθητές μας τη διαφορά από τη θεωρητική τιμή με τους μαθητές μας καλώντας τους να εκφέρουν άποψη για το «σφάλμα». Καθοδηγούμε την αναζήτηση του γιατί προκύπτει σφάλμα στις μετρήσεις, στη μέτρηση της γωνίας και του ύψους αλλά περισσότερο στο σφάλμα αντίδρασης κατά τις μετρήσεις του χρόνου

Τους καλούμε στη συνέχεια να κάνουν με παρόμοιο τρόπο μετρήσεις για το κυλινδρικό κέλυφος, για τον συμπαγή κύλινδρο και για τον δακτύλιο και συζητάμε τα αποτελέσματα

4. Αξιολόγηση

Προτείνουμε στους μαθητές τρία ζητήματα για να τα επεξεργαστούν μόνοι τους.

Στο πρώτο τους ζητάμε να υπολογίσουν θεωρητικά τη ροπή αδράνειας ενός ομογενούς δακτυλίου ως προς άξονα κάθετο στο επίπεδό του που περνάει από το κέντρο μάζας

Στο δεύτερο τους καλούμε να συγκρίνουν τους χρόνους κύλισης από την κορυφή μέχρι τη βάση ενός κεκλιμένου επιπέδου μιας μεγάλης και μιας μικρότερης σφαίρας με δεδομένου ότι και οι δύο είναι ομογενείς .

Στο τρίτο τους ζητάμε να υπολογίσουν την επιτάχυνση του κέντρου μάζας ενός ομογενούς κυλίνδρου κατά την κίνησή του σε κεκλιμένο επίπεδο με φορά προς τα πάνω.

Η - μέσα από τη διδασκαλία - οικοδόμηση της έννοιας ΡΟΠΗ ΑΔΡΑΝΕΙΑΣ

Το πρώτο βήμα. Η ΕΜΠΕΙΡΙΑ

Η εμπειρία – μνήμη. Τον είχε δει με τα μάτια του και διατηρείται στη μνήμη του αναλλοίωτο. Τον τολμηρό ισορροπιστή σε οριζόντιο τεντωμένο σκοινί, πάνω από τον Ισθμό στην Κόρινθο, σε ύψος εκατό περίπου μέτρων, να μετακινείται αργά αλλά να μετακινείται . Και μια λεπτομέρεια που δεν είναι και τόσο λεπτομέρεια . Μετακινούμενος κρατά μια τεράστιου μήκους ράβδο και τη διατηρεί κάθετη στην κατεύθυνση της κίνησής του. Η εμπειρία έχει διδάξει κάθε ακροβάτη ότι με αυτό τον τρόπο η «αντίσταση» στο να στραφεί περί άξονα που συμπίπτει με το σκοινί και να κινδυνεύσει είναι ιδιαιτέρως μεγάλη.

Η εμπειρία θέαση καλλιτεχνικού πατινάζ . Στην οθόνη καλλιτεχνικό πατινάζ πάνω σε πάγο και ο Γεβγκένι Πλάσενκα, επιβάλλει στο σώμα του στροφική κίνηση περί κατακόρυφο άξονα, μαζεύει τα χέρια του και περιστρέφεται πιο γρήγορα, τεντώνει τα χέρια και στρέφεται πιο αργά

Η μάζα του διατηρείται σταθερή, οι εξωτερικές δυνάμεις περίπου ασήμαντες κι όμως αλλάζει η στροφική κινητική του κατάσταση.

Η εμπειρία «κατάδυση από βατήρα». Ολυμπιακοί αγώνες και το άθλημα των καταδύσεων. Η αθλήτρια ζυγιάζεται στον βατήρα, εκτινάσσεται, το σώμα της ακολουθεί μια διαδρομή προς τα πάνω, στη συνέχεια εκτελεί στροφική κίνηση και για να την καταφέρει μαζεύει το σώμα της εντυπωσιακά, το μαζεύει γύρω από το κέντρο μάζας όσο γίνεται περισσότερο έτσι ώστε να «προλάβει» γιατί ο χρόνος της όλη διαδρομής είναι πολύ λίγος .

Την παρακολουθούμε και αναρωτιόμαστε γιατί το κάνει αυτό.

Η εμπειρία στο σχολικό εργαστήριο. Ο συμπαγής κύλινδρος και ο κούφιος κύλινδρος σε κεκλιμένο επίπεδο αφήνονται ταυτόχρονα και στον αγώνα δρόμου ο συμπαγής βγαίνει πάντα νικητής, κατεβαίνει πιο γρήγορα ανεξάρτητα από το εάν έχει μεγαλύτερη ή μικρότερη μάζα από τον άλλο. Η μπίλια – σφαίρα και ο συμπαγής κύλινδρος στον επόμενο αγώνα δρόμου στο κεκλιμένο επίπεδο και η μπίλια κατεβαίνει πάντοτε πρώτη ανεξάρτητα από τη σχέση των μαζών των δύο σωμάτων. Συζήτηση για τα δύο γεγονότα. Ερωτήματα.

Το δεύτερο βήμα. Επίκληση της ιδέας ότι η μάζα ενός σώματος είναι μέτρο της «δυσφορίας» του στο να αλλάξει η κινητική του κατάσταση. Η ανεπάρκεια της μάζας στο να εκφράσει τη δυσφορία στις αλλαγές σε περίπτωση που το ακίνητο σώμα θα ενεργοποιηθεί σε στροφική κίνηση. Επίκληση της ιδέας ότι η ενεργοποίηση ενός ακίνητου σώματος σε στροφική κίνηση απαιτεί ροπή. ροπή. Η οικοδόμηση – από τον Euler – μιας καινούργιας έννοιας η οποία θα συμπεριλάβει τη μάζα αλλά θα καταγράφει και το πώς κατανέμεται η μάζα σε σχέση με τον άξονα της επικείμενης περιστροφής. Από τον δεύτερο νόμο του Newton στον νόμο για τη στροφική κίνηση. Το σώμα θεωρείται σύνολο υλικών σημείων μαζών m₁, m₂, m₃, . . . m_ν .

Αποδεικνύεται ότι η γωνιακή επιτάχυνση είναι ανάλογη προς την ολική ροπή αλλά η τιμή της εξαρτάται και από την τιμή μιας «παράξενης ποσότητας» ίσης με το άθροισμα κάποιων θετικών ποσοτήτων . Κάθε θετική ποσότητα αντιστοιχεί σε κάθε υλικό σημείο του σώματος και είναι ίση με το γινόμενο της μάζας m_i του υλικού αυτού σημείου επί το τετράγωνο της απόστασής του r_i² από τον άξονα m_ir_i². Η «παράξενη θετική ποσότητα» αναφέρεται στο συγκεκριμένο σώμα και σε συγκεκριμένο άξονα, λέγεται ροπή αδράνειας ως προς τον άξονα και συμβολίζεται με το γράμμα Ι, αρχικό του λατινικού Inertia –αδράνεια . Όσο για το τι εκφράζει καταδεικνύεται στην εξίσωση που προκύπτει ( νόμος για τη στροφική κίνηση ή νόμος του Euler ) α_γων = τ_ολ/Ι .

Για ορισμένη ολική ροπή όσο μεγαλύτερη είναι η ροπή αδράνειας τόσο μικρότερη θα είναι η γωνιακή επιτάχυνση. Σύγκριση με τον δεύτερο νευτωνικό νόμο της κίνησης για υλικό σημείο ή και για σώμα σε μεταφορική κίνηση α_cm = F_ολ/m.

Το τρίτο βήμα. Αν το σώμα είναι ομογενές σε σχήμα δακτυλίου χωρίς πάχος , ακτίνας R, η ροπής αδράνεια ως προς άξονα κάθετο στο επίπεδο του δακτυλίου διερχόμενο από το κέντρο μάζας του, μπορεί εύκολα να υπολογιστεί. Το σώμα

μπορεί να θεωρηθεί σύνολο υλικών σημείων τα οποία ισαπέχουν από τον άξονα, οπότε

Ι = (m₁R² + m₂ R² + m₃ R² + . . . . m_nR²) = (m₁ + m₂ + m₃ + . . . . m_n) R².

Αλλά το άθροισμα των μαζών των υλικών σημείων που το συναποτελούν είναι ίσο με τη μάζα m του σώματος, άρα Ι_cm = mR²

Αν το σώμα είναι ομογενές σε σχήμα γεωμετρικό, όπως μία ράβδος, ένας κύλινδρος ή μια σφαίρα η ροπή αδράνειας ως προς άξονα που περνά από το κέντρο μάζας είναι δυνατόν να υπολογιστεί με βάση την έννοια ολοκλήρωμα . Αν το σώμα έχει σχήμα σφαίρας προκύπτει Ι_cm = (2/5) mR² , αν έχει σχήμα ορθού κυλίνδρου η ροπή αδράνειας ως προς τον άξονα συμμετρίας τον κάθετο στις δύο βάσεις προκύπτει Ι_cm = ½mR²½ εάν έχει σχήμα μονοδιάστατης ράβδου, μήκους ℓ, η ροπή αδράνειας ως προς τον άξονα συμμετρίας τον κάθετο στη διεύθυνσή της προκύπτει ίση με (1/12)mℓ² .

Το τέταρτο βήμα. Ένα σώμα και ένα σύνολο αξόνων οι οποίοι είναι μεταξύ τους παράλληλοι. Αναφορικά με καθένα από αυτούς το σώμα έχει και μία συγκεκριμένη ροπή αδράνειας. Αποδεικνύεται γεωμετρικά ότι η τιμή της ροπής αδράνειας ως προς κάποιον άξονα εξαρτάται από την απόσταση του άξονα από το κέντρο μάζας σύμφωνα με το λεγόμενο θεώρημα των παραλλήλων αξόνων, το οποίο πρότεινε τον 19^ο αιώνα ( 1830) ο μαθηματικός Jacob Steiner, Γιακόμπ Στάινερ.

Επισημαίνεται ότι με βάση το θεώρημα, η ροπή αδράνειας ενός σώματος ως προς άξονα Α_cm διερχόμενο από το κέντρο μάζας έχει τη μικρότερη από όλες τις ροπές αδράνειας που παρουσιάζει το σώμα ως προς οποιονδήποτε άλλο άξονα παράλληλο προς τον Α_cm.

Το πέμπτο βήμα . Η ροπή αδράνειας και η κινητική ενέργεια του στρεφόμενου σώματος. Το σώμα σε στροφική κίνηση περί άξονα το «αντιμετωπίζει» ως σύνολο υλικών σημείων με ίσες γωνιακές ταχύτητες. Η κινητική του ενέργεια θα είναι άθροισμα των κινητικών ενεργειών των υλικών σημείων που το συγκροτούν.

Το άθροισμα οδηγεί στην τιμή ½ επί τη γωνιακή ταχύτητα στο τετράγωνο επί μία θετική ποσότητα. Κ = ½ω²( m₁r_i² + m₂r₂² + m₃r₃² + . . . . m_nr_n².) Η θετική αυτή ποσότητα είναι η ροπή αδράνειας . Συμμετέχει στη διαμόρφωση της τιμής της κινητικής ενέργειας Κ = ½Ιω² με τρόπο παρόμοιο με εκείνο που η μάζα συμμετέχει στη διαμόρφωση της τιμής της κινητικής ενέργειας του σώματος σε κίνηση μεταφορική ( Κ = ½mυ²)

Το έκτο βήμα. Η ροπή αδράνειας και η στροφορμή του σώματος σε στροφική κίνηση.

Το σώμα σε στροφική κίνηση, περί άξονα z, το «αντιμετωπίζει» ως σύνολο υλικών σημείων με ίσες γωνιακές ταχύτητες ω. Η στροφορμή του ως προς την των αξόνων Ο θα είναι διανυσματικό άθροισμα των στροφορμών -ως προς την αρχή των αξόνων - των υλικών σημείων που το συγκροτούν. Το άθροισμα οδηγεί σε ένα διάνυσμα με μέτρο ίσο με το γινόμενο της γωνιακής ταχύτητας επί μια θετική ποσότητα. Η θετική αυτή ποσότητα είναι και πάλι η ροπή αδράνειας του σώματος ως προς τον άξονα z της περιστροφής. L = Iω .

Το έβδομο βήμα. Η μέτρηση της ροπής αδράνειας στο εργαστήριο. Η μέτρηση μπορεί να πραγματοποιηθεί με το να επιλέξουμε ένα φαινόμενο κίνησης την οποία να εκτελεί το σώμα και να εφαρμόσουμε κατάλληλα νόμους της συγκεκριμένης κίνησης στους οποίους να συμμετέχει και η ροπή αδράνειας . Μια καλή επιλογή είναι η κίνηση του σώματος να είναι κύλιση χωρίς ολίσθηση σε κεκλιμένο επίπεδο. Θα χρειαστούμε χρονόμετρο, , μετροταινία και ζυγό . Αν το σώμα είναι κύλινδρος ,

Για την κύλιση ισχύει Τ_σR = I_cm αγ_ων , mgημθ – Τ_σ = mα_cm ,

α_γων = α_cm/R και

για την κίνηση του κέντρου μάζας x = ½α_cmt². Προκύπτει

I_cm = mR²( gημθt²/2x- 1)

Με τη μετροταινία μπορούμε να μετρήσουμε τη μετατόπιση του κέντρου μάζας x και να προσδιορίσουμε την εφθ άρα και το ημθ. Με τη μετροταινία – ακόμα καλύτερα με παχύμετρο - μπορούμε να μετρήσουμε τη διάμετρο άρα και την ακτίνα της βάσης.

Το όγδοο βήμα.

Επιστροφή στις εμπειρίες του βήματος ένα και απόπειρα να ερμηνευτούν τα φαινόμενα .

Με βάση την έννοια ροπή αδράνειας και τον νόμο της στροφικής κίνησης μπορούμε να εξηγήσουμε την εμπειρία σώματος, την εμπειρία μνήμη με τον ακροβάτη και να δώσουμε απάντηση στα ερωτήματα που δημιούργησε η κατάδυση, η κύλιση των κυλίνδρων και η κυλιόμενη μπίλια.

Αποδεχόμενοι ότι με το να «μαζέψει» τα χέρια ο χορευτής ή η χορεύτρια ελαττώνεται η ροπή αδράνειας και βασιζόμενοι στη διατήρηση της στροφορμής μπορούμε να δώσουμε μια εξήγηση στο «γιατί αυξάνεται η γωνιακή ταχύτητα κάθε χορευτή όταν μαζεύει τα χέρια» .

Με ανάλογο τρόπο μπορούμε να οδηγηθούμε σε μια εξήγηση του γιατί η κολυμβήτρια μαζεύει το σώμα της γύρω από το κέντρο μάζας με αποτέλεσμα να ελαχιστοποιήσει τη ροπή αδράνειας ως προς οριζόντιο άξονα που περνά από το κέντρο μάζας και να κάνει σε όσο γίνεται λιγότερο χρόνο την περιστροφή περί άξονα που περνά από το κέντρο μάζας του σώματός της

Το ένατο βήμα. Μεταβαλλόμενη ροπή αδράνειας . Όταν η χορεύτρια μαζεύει τα χέρια ελαττώνεται η ροπή αδράνειας με συνέπεια να αυξάνεται η γωνιακή της επιτάχυνση μολονότι η ολική εξωτερική ροπή είναι μηδενική.

Ο νόμος για τη στροφική κίνηση στη γενικότερη μορφή του τ = dL/dt, - αντίστοιχος προς το δεύτερο της κίνησης με τη γενικότερη επίσης μορφή του F = dp/dt – μπορεί να ερμηνεύσει το γεγονός ότι η μεταβολή και μόνο της ροπής αδράνειας σε ένα στρεφόμενο σύστημα ( μια χορεύτρια σε στροφική κίνηση ή ένας στρεφόμενος μύλος στην παιδική χαρά και το παιδί να μετακινείται πάνω του) έχει ως αποτέλεσμα την εμφάνιση γωνιακής επιτάχυνσης, χωρίς τη δράση εξωτερικής ροπής.

τ = d(Ιω)/dt τ = Ιdω/dt + ωdI/dt , εξίσωση στην οποία διακρίνει κανείς εύκολα ότι ακόμα και εάν τ = 0 προκύπτει dω/dt = - (ω/Ι) (dI/dt) .

Το δέκατο βήμα. Σφόνδυλος . Τροχός με μεγάλη ροπή αδράνειας.

Οι Γάλλοι τον λένε « βολάν αδράνειας» volant d'inertie ή απλά βολάν, οι Άγγλοι Flywheel.

Οι έλληνες μηχανικοί τον λένε σφόνδυλο.

Έχει ένα μεγάλο μέρος της μάζας του

στην περιφέρεια του τροχού οπότε

η ως προς άξονα περιστροφής διερχόμενο

από το κέντρο μάζας τιμή της ροπής αδράνειας να πλησιάζει το mR² .

Μπορεί και αποθηκεύει συγκριτικά μεγάλες ποσότητες κινητικής ενέργειας.

Αξιοποιείται και για να σταθεροποιεί στρεφόμενες διατάξεις όπως οι δορυφόροι και τα γυροσκόπια

Παραπομπές

1. Ροπή της μάζας- αδράνειας, στις γλώσσες του Κόσμου. Με τρεις λέξεις, με δύο λέξεις, με μία λέξη. Σε Σε όλες τις ευρωπαϊκές γλώσσες η νέα έννοια θεωρείται «ροπή» κάποιας άλλης φυσικής ποσότητας,

η οποία εν προκειμένω είναι η - με μοναδικό μέτρο τη μάζα – αδράνεια.

Σε ορισμένες ευρωπαϊκές γλώσσες ο όρος συγκροτείται από τρεις λέξεις. Η μία με σημαινόμενο τη γενικότερη έννοια «ροπή», η άλλη με σημαινόμενο τη φυσική ποσότητα «αδράνεια-μάζα» αλλά οι δύο αυτές λέξεις συνδέονται και με άρθρο δηλωτικό της γενικής πτώσης, αγγλικά «of», γαλλικά «de» -γίνεται «d’», ιταλικά «di», ισπανικά και ρουμάνικα «de», αλβανικά «i»..

Στα αγγλικά η ροπή είναι moment, η αδράνεια inertia και η ροπή αδράνειας moment of inertia,

στα γαλλικά η ροπή moment, η αδράνεια inertie και η ροπή αδράνειας moment d'inertie,

στα ιταλικά η ροπή momento, η αδράνεια inerzia και η ροπή αδράνειας momento di inerzia ,

στα ισπανικά η ροπή momento, η αδράνεια inercia και η ροπή αδράνειας momento de inercia,

στα ρουμάνικα η ροπή momentul, η αδράνεια inerție, η ροπή αδράνειας momentul de inerție,

στα αλβανικά η ροπή momenti, η αδράνεια inerci και η ροπή αδράνειας momenti i inercisë

Στην ελληνική, στην τουρκική, στις σλαβικές γλώσσες και στις βαλτικές γλώσσες, είτε το άρθρο περιττεύει διότι η γενική υποδηλώνεται και χωρίς αυτό, είτε δεν υφίσταται άρθρο, οπότε ο όρος διαμορφώνεται από δύο λέξεις .

Στην τουρκική, η ροπή momenti, η αδράνεια eylemsizli, η ροπή αδράνειας eylemsizlik momenti

Στη ρωσική, момент, инерция ( ίνερτσεγιά ) και момент инерции ( μόμιεντ ινέρτσε)

Στη βουλγαρική, момент, инерция (ινέρτσιγια ) και инерционен момент ( ινερτσιόνεν μόμεντ)

Στην πολωνική η ροπή moment, η αδράνεια inerjia - bezwładność η ροπή αδράνειας moment bezwładności

Στη γλώσσα των Τσέχων, η ροπή moment, η αδράνεια setrvačnost, η ροπή αδράνειας moment setrvačnosti

στη γλώσσα των Λιθουανών inerces moments , στη γλώσσα των Λεττονών inerces moments

Σε γλώσσες διαμορφωμένες από επιδράσεις της γερμανικής ο νέος όρος αποδίδεται με μία λέξη.

προϊόν συγκρυστάλλωσης των δύο αντίστοιχων λέξεων με σημαινόμενα τη ροπή και την αδράνεια

Στα γερμανικά, η ροπή Moment, η αδράνεια Trägheit και η ροπή αδράνειας Trägheitsmoment

στα ολλανδικά, η ροπή moment η αδράνεια traagheid η ροπή αδράνειας traagheidsmoment

στα σουηδικά, η ροπή είναι moment η αδράνεια tröghet, και η ροπή αδράνειας tröghetsmoment,

στα δανέζικα, η ροπή moment η αδράνεια inerti , η ροπή αδράνειας inertimoment

στα νορβηγικά, η ροπή moment, η αδράνεια treghet , η ροπή αδράνειας treghetsmoment

Με μία λέξη αποδίδεται και στις γλώσσες των Φιλανδών και των Εσθονών,

στα φιλανδικά inertiamomentti, τα εσθονικά inertsimoment