Ανδρέας Ιωάννου Κασσέτας

Η έννοια Ροπή δύναμης

1.  Προσωπικές αναμνήσεις .

Τότε με τον θείο τον Νώντα στην παιδική χαρά, εκείνος οκτώ ετών στην τραμπάλα και ο θείος  στην πλευρά την απέναντι αφού προηγουμένως είχε φροντίσει να μετακινήσει την τραμπάλα έτσι ώστε να μη στηρίζεται στο μέσον και εκείνος ο οκτώ ετών, λιγότερο από τριάντα κιλά, κέρδιζε τον πελώριο θείο της άλλης πλευράς. Μάλιστα τέντωνε και το σώμα προς τα πίσω για να καταφέρει να τον νικήσει και η τραμπάλα να στραφεί προς το μέρος του. Κάτι παρόμοιο είχε δει και στο Σινεάκ με Χοντρό Λιγνό.  

2. Η καταγωγή της έννοιας.

Τα βασικά εμπειρικά στοιχεία με τα οποία οικοδομήθηκε η έννοια ροπή δύναμης εμπεριέχονται στο έργο  στοχαστών από τους ελληνιστικούς χρόνους, στον χρυσό κανόνα της Μηχανικής και στο έργο του Αρχιμήδη για τη δυνατότητα να  αυξάνουμε μια δύναμη με τον μοχλό. Ο λεγόμενος «νόμος του μοχλού» εισάγει και τις έννοια «μοχλοβραχίονας δύναμης» σχετιζόμενη με την εμπειρία του ανθρώπινου βραχίονα  και αναφέρεται σε ισότητα των δύο γινομένων «δύναμη επί μοχλοβραχίονα». Σε παρόμοια θεώρηση η  οποία περιλάμβανε τα βασικά στοιχεία της ροπής στηρίχτηκε και η ακρίβεια του πανάρχαιου ζυγού . Η έννοια δύναμη, βέβαια δεν συμμετέχει με τον νευτωνικό ορισμό της .

Το ζήτημα απασχόλησε και τον Λεονάρντο ντα Βίντσι αλλά και τον Γαλιλαίο.

α. Η Νέα Μηχανική του Πιερ Βαρινιόν

Μετά τον νευτωνικό ορισμό της έννοιας δύναμη, η έννοια «ροπή δύναμης» - δεν ορίζεται στα Pricipia  - εισάγεται σε γλώσσα γαλλική ως moment d’ une force ( ροπή μιας δύναμης ως προς σημείο ) από τον Πιερ Βαρινιόν -Pierre Varignon-

Το 1687, ένα περίπου έτος μετά την εμφάνιση της πρώτης έκδοσης του νευτωνικού Principia , ο Varignon στο PROJECT D’UNE NOUVELLE MECHANIQUE- Σχέδιο για μια Νέα Μηχανική – παρουσιάζει την εργασία του πάνω στη Νέα Μηχανική συνδυάζοντας εμπειρικά στοιχεία, Γεωμετρία και ψήγματα από τον νεογέννητο Διαφορικό λογισμό. Στη νέα αυτή Μηχανική παρουσιάζει και τον κανόνα του παραλληλογράμμου για τη σύνθεση δύο δυνάμεων τον οποίο έχει ήδη παρουσιάσει στα Corollaries 1 και 2 ο Isaac Newton. Βέβαια η λογική του συγκεκριμένου κανόνα είχε διατυπωθεί έναν περίπου αιώνα πριν από τον πρωτοπόρο Φλαμανδό Simon Stevin.

β.H έννοια ΡΟΠΗ ΔΥΝΑΜΗΣ

και το ΘΕΩΡΗΜΑ ΤΩΝ ΡΟΠΩΝ

Τα χρόνια που ακολουθούν ο Varignon θα ενδιαφερθεί ιδιαίτερα για την έννοια ΡΟΠΗ ΔΥΝΑΜΗΣ – Moment d’ une force – αποδίνοντάς της ένα ιδιαίτερο ρόλο στη θεωρητική μελέτη του φαινομένου «ισορροπία» και αποδίδοντας της 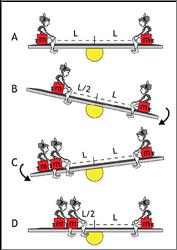τη φυσική σημασία μιας έννοιας η οποία καταγράφει την ικανότητα της αντίστοιχης δύναμης στο να συμβάλει¹ στη διαμόρφωση της στροφικής κίνησης ενός αρχικά ακίνητου σώματος στο οποίο ασκείται. Συγκεκριμένα αν φανταστούμε ένα μηχανικό στερεό ένα σημείο Α του οποίου διατηρείται αμετακίνητο και ασκηθεί μία δύναμη σε αυτό το η «ικανότητα»της δύναμης να προκαλέσει – σε συνεργασία με το γεγονός ότι το σώμα στηρίζεται μόνο στο σημείο Α- μια λιγότερο ή περισσότερο έντονη στροφική κίνηση στο συγκεκριμένο σώμα δεν εξαρτάται μόνο από την τιμή της δύναμης, ούτε μόνο από την τιμή απόστασης. Η σχετική εμπειρία διδάσκει ότι η ικανότητα αυτή εξαρτάται από το γινόμενο «δύναμη επί την απόσταση του σημείου Α από τον φορέα της

Παράλληλα, ο Βαρινιόν, παρουσιάζει και την απόδειξη του θεωρήματος των ροπών. Βασιζόμενος στον κανόνα του παραλληλογράμμου και σε Ευκλείδεια Γεωμετρία αποδεικνύει² ότι το άθροισμα των ροπών ενός συνόλου δυνάμεων ως προς κάποιο σημείο - είναι ίσο με την , ως προς το ίδιο σημείο, ροπή της συνισταμένης τους.

Το θεώρημα εξακολουθεί να αναφέρεται ως θεώρημα του Varignon. Με το θεώρημα των ροπών μπορούμε να προσδιορίσουμε τη συνισταμένη δύο δυνάμεων με παράλληλους φορείς³. Χωρίς αυτό δεν μπορούμε.

Ωστόσο η παρουσίαση της έννοιας ΡΟΠΗ ΔΥΝΑΜΗΣ και του σχετικού θεωρήματος γίνεται στο MECHANIQUE NOUVELLE ou STATIQUE , στο οποίο παρουσιάζεται ολόκληρο το έργο του αλλά κυκλοφορεί το 1725, τρία δηλαδή χρόνια μετά τον θάνατό του.

Την επόμενη χρονιά ο Daniel Bernoulli αναφέρεται και αυτός στην έννοια , σε γλώσσα γερμανική⁴.

Οι αγγλόφωνοι θα την ονομάσουν Moment of a force. Ο όρος moment θα επικρατήσει στις περισσότερες ευρωπαϊκές γλώσσες, ως moment , αλλά και με τις παραλλαγές momento ( στη γλώσσα των Ιταλών, των Ισπανών και των Πορτογάλων ), στη γλώσσα των Ρουμάνων momentul, στα αλβανικά και στα τούρκικα momenti, στα φινλανδική voimamomentti ( ροπή δύναμης) στη γλώσσα των Λιθουανών momentas jėga ( ροπή δύναμης) .

Η έννοια Ροπή δύναμης

αναφέρεται σε δύναμη ασκούμενη σε κάποιο σώμα και

σε ένα γεωμετρικό σημείο Α.

Ορίζεται ως εξωτερικό γινόμενο του διανύσματος «θέση του σημείου Α», σε συγκεκριμένο σύστημα αναφοράς, επί το διάνυσμα «δύναμη».

Ορίζεται, με άλλο λόγια, ως διάνυσμα

με μέτρο το «γινόμενο του μέτρου της δύναμης επί την απόσταση του σημείου Α από τον φορέα της δύναμης». Η διεύθυνση του διανύσματος είναι κάθετη στο επίπεδο που ορίζει ο φορέας της δύναμης και το σημείο Α. Η φορά της ορίζεται ως φορά της μετακίνησης ενός αρχικά ακίνητου δεξιόστροφου κοχλία εάν στραφεί κατά τη φορά που η ασκούμενη στο σώμα δύναμη τείνει να στρέψει το αρχικά ακίνητο αυτό σώμα περί άξονα που συμπίπτει με τον φορέα του διανύσματος της ροπής.

γ. Η έννοια «ολική ροπή» και η αλγεβρική τιμή της

Η έννοια ολική ροπή ενός συνόλου δυνάμεων ως προς σημείο Α έχει νόημα μόνο εφόσον οι αντίστοιχες δυνάμεις ασκούνται στο ίδιο σώμα.

Αν περιοριστούμε σε δυνάμεις συνεπίπεδες με το σημείο Α να ανήκει στο επίπεδό τους, τα διανύσματα των αντίστοιχων ροπών θα έχουν το ίδιο φορέα κάθετο στο επίπεδο των δυνάμεων στο σημείο Α. Αν στη θέση αυτού του φορέα θεωρήσουμε άξονα z μπορούμε να αναφερόμαστε στην ΑΛΓΕΒΡΙΚΗ ΤΙΜΗ κάθε ροπής – με πρόσημο + ή – ανάλογα με τη φορά της αντίστοιχης ροπής σε σχέση με τον άξονα. Το άθροισμα των αλγεβρικών τιμών των ροπών θα συνιστά το λεγόμενο «αλγεβρικό άθροισμα των ροπών» ή την αλγεβρική τιμή της ολικής ροπής. Συνήθως τη συμβολίζουμε με «τ_ολ».

3. Ζεύγος δυνάμεων.

α. Τι συμβαίνει με τη συνισταμένη τους ;

Δύο δυνάμεις αντιπαράλληλες με ίσα μέτρα ασκούνται στο ίδιο σώμα, στη γλώσσα της Φυσικής ένα «ζεύγος δυνάμεων» . Τι συμβαίνει με τη συνισταμένη τους ;

Λέει ο φυσικός Α : Η συνισταμένη των δύο δυνάμεων θα είναι η μηδενική δύναμη .Εξ άλλου, στο επίπεδο των δυνάμεων, ΣF_X = 0    ΣF_Y=0

 Λέει ο Β :  Δεν συμφωνώ. Εκτιμώ ότι στην περίπτωση ζεύγους «συνισταμένη των δύο αυτών δυνάμεων» δεν υφίσταται. Κι αυτό διότι δεν υφίσταται ως έννοια η ΜΙΑ εκείνη δύναμη – ούτε και η μηδενική δύναμη στην οποία αναφέρεσαι – η οποία να προκαλεί το μηχανικό αποτέλεσμα που προκύπτει από τη συνεργασία των δύο αυτών δυνάμεων. Σε ένα ακίνητο. λόγου χάρη,  σώμα η μηδενική δύναμη προκαλεί διατήρηση της ακινησίας και στην περίπτωση του ζεύγους αυτό δεν συμβαίνει.   

 ο Α : Σύμφωνα με τη δική μου άποψη η έννοια «συνισταμένη δύο δυνάμεων⁵» έχει ως σημαινόμενο τη μία εκείνη δύναμη, η οποία καθορίζει τη μεταβολή της ορμής και στην περίπτωση του ζεύγους η ορμή του σώματος διατηρείται, δεν μεταβάλλεται.

Να προσθέσω και ότι για σώμα με σταθερή μάζα – dm/dt = 0 – η συνισταμένη των δύο δυνάμεων, σε συνδυασμό με την αδράνεια του σώματος, καθορίζει την επιτάχυνση του κέντρου μάζας.  Θεωρώ δηλαδή ως εξίσωση ορισμού της συνισταμένης F_R την F_R = ma_cm .  Στην περίπτωση της δράσης των δύο δυνάμεων του ζεύγους η επιτάχυνση που προκύπτει για το κέντρο μάζας είναι μηδενική.

 ο Β : Η δική μου άποψη είναι διαφορετική:  Το κοινό στοιχείο ανάμεσα στις έννοιες «ζεύγος δυνάμεων» και «συνισταμένη μηδέν» είναι  ότι και στις δύο περιπτώσεις το κέντρο μάζας του σώματος έχει μηδενική επιτάχυνση .

Η ιδιαιτερότητα όμως της έννοιας «ζεύγος δυνάμεων» και η διάκρισή της από την έννοια «μηδενική δύναμη» σχετίζεται και με το ότι «η δράση ενός ζεύγους για οποιοδήποτε dt συνεπάγεται μεταβίβαση ενέργειας» κάτι που δεν συμβαίνει με το «συνισταμένη μηδέν», συνεπάγεται όμως και μεταβολή στροφορμής κάτι που επίσης δεν συμβαίνει με το «συνισταμένη μηδέν». Εκτιμώ ότι ένα σύνολο ομοεπιπέδων δυνάμεων ασκουμένων στο ίδιο σώμα μπορεί να αναχθεί : α. σε μία και μόνο δύναμη    β. σε μηδενική δύναμη γ. σε δύο αντιπαράλληλες δυνάμεις ίσων μέτρων, στο λεγόμενο ζεύγος.

Η μηδενική δύναμη σχετίζεται με τον νόμο της αδράνειας. Εφόσον η ασκούμενη δύναμη σε κινούμενο σώμα σταθερής μάζας είναι μηδενική η κίνηση θα είναι αδρανειακή. Ευθύγραμμη ομαλή αν πρόκειται για υλικό σημείο, μεταφορική κίνηση με μηδενική επιτάχυνση αν πρόκειται για σώμα σε μεταφορική κίνηση,  κίνηση με σταθερή γωνιακή ταχύτητα αν πρόκειται για στρεφόμενο στερεό, είτε και κύλιση με σταθερή ταχύτητα του κέντρου μάζας. Σε κάθε περίπτωση – στα πλαίσια πάντα της κλασικής φυσικής –κίνηση χωρίς μεταβίβαση ενέργειας, κίνηση με σταθερή στροφορμή .  Η δράση ενός ζεύγους δυνάμεων σε σώμα με διαστάσεις δεν συνεπάγεται αδρανειακή κίνηση.   

 β. Η έννοια «ζεύγος δυνάμεων»

H έννοια «ζεύγος δυνάμεων» έχει διαφορετικό ρόλο από την έννοια « μηδενική δύναμη» . Οι αλγεβρικές δομές ΣF_x = 0 και ΣF_y = 0 εξασφαλίζουν τη μηδενική επιτάχυνση του κέντρου μάζας γεγονός που σημαίνει ότι το σύνολο των ασκουμένων στο σώμα δυνάμεων ισοδυναμεί είτε με «συνισταμένη μηδέν» είτε με «ζεύγος». Αν το αντικείμενο είναι υλικό σημείο θα διατηρήσει την ταχύτητά του. Αν όμως είναι μηχανικό στερεό για να περιγραφεί η «διατήρηση της κινητικής του κατάστασης ως προς κάποιο σύστημα αναφοράς»- μηδενική ταχύτητα για κάθε σημείο του, μεταφορική κίνηση με σταθερή ταχύτητα του κέντρου μάζας, στροφική κίνηση με σταθερή γωνιακή ταχύτητα, κύλιση με σταθερή ταχύτητα του κέντρου μάζας - απαιτείται και μία ακόμα αλγεβρική σχέση. Αυτή είναι η σχέση που καταγράφει ότι η ολική ροπή είναι ίση με μηδέν, σχέση που η οποία αποκλείει την ισοδυναμία με ζεύγος. Και όλα αυτά για δυνάμεις ομοεπίπεδες.

Ένα σύνολο δυνάμεων ασκουμένων στο ίδιο σώμα μπορεί – μέσα από διεργασία σύνθεσης των δυνάμεων αυτών ανά δύο - να αναχθεί

α. σε μία και μόνο δύναμη –συνισταμένη- β. σε μηδενική συνισταμένη δύναμη

γ. σε δύο αντιπαράλληλες δυνάμεις ίσων μέτρων, στο λεγόμενο ζεύγος .

α. Εφόσον για τις δυνάμεις αυτές υφίσταται συνισταμένη «η ολική ροπή ως προς Α είναι ίση με την, ως προς Α, ροπή της συνισταμένης». Η τιμή συνεπώς της ολικής ροπής ΕΞΑΡΤΑΤΑΙ ΑΠΟ ΤΗ ΘΕΣΗ ΤΟΥ Α και δεν μπορούμε να μιλάμε για «ροπή» αλλά για «ροπή ως προς συγκεκριμένο σημείο Α». Η ολική λόγου χάρη ροπή ως προς κάθε γεωμετρικό σημείο που ανήκει στην ευθεία-φορέα της συνισταμένης θα είναι ίση με μηδέν.

β. Εφόσον η συνισταμένη των ασκουμένων δυνάμεων είναι μηδενική η ολική ροπή θα είναι μηδενική ως προς κάθε σημείο

γ. Εάν όμως η σύνθεση των ασκουμένων αυτών δυνάμεων οδηγεί σε ΖΕΥΓΟΣ , η ολική ροπή ως προς οποιοδήποτε σημείο έχει την ίδια τιμή, ανεξάρτητα από τη θέση του σημείου . Σε αυτή την περίπτωση μπορούμε να μιλάμε για «ροπή» χωρίς καμία αναφορά σε σημείο ή – ισοδύναμα – για ροπή ζεύγους.

4.Ροπή δύναμης ως προς σημείο και «Ροπή»⁶

Μία έννοια ή δύο έννοιες;

Ήδη από τον 18^ο αιώνα τόσο οι φυσικοί όσο και οι μηχανικοί, κυρίως οι αγγλόφωνοι, είχαν προχωρήσει στη διάκριση ανάμεσα στις έννοιες Moment of a force - στα ελληνικά ροπή δύναμης, αναφερόμενη σε γεωμετρικό σημείο - και Torque  - στα ελληνικά «ροπή ζεύγους» ή «ροπή» .

H Torque αναφέρεται μόνο σε ζεύγος δυνάμεων, είναι ίση με το άθροισμα των ροπών ως προς οποιοδήποτε γεωμετρικό σημείο και είναι μια ειδική περίπτωση της ευρύτερης έννοιας Moment, έννοια με «δικές της ιδιότητες» .  Ενώ η  Moment of a force ροπή μιας δύναμης αναφέρεται σε γεωμετρικό σημείο, η Torque ροπή ζεύγους δεν αναφέρεται σε γεωμετρικό σημείο.

Στην εποχή μας, οι  περισσότεροι φυσικοί στις Ηνωμένες Πολιτείες τόσο για τη «ροπή δύναμης ως προς σημείο» όσο και για τη «ροπή ζεύγους», χρησιμοποιούν τον  όρο Torque. Μάλιστα το αρχικό της λέξης, στην ελληνική του εκδοχή – γράμμα  «τ »-  θα χρησιμοποιηθεί ως σύμβολο, αν και οι περισσότεροι ευρωπαίοι προκειμένου για ροπή δύναμης χρησιμοποιούν το κεφαλαίο Μ αρχικό της λέξης Moment

Σε πολλές αναρτήσεις στο Διαδίκτυο τα  Moment of a force και Torque  θεωρούνται συνώνυμα. Ωστόσο οι πιο προσεκτικοί φυσικοί επισημαίνουν ότι το Moment of a force αναφέρεται σε δύναμη και σε γεωμετρικό σημείο ενώ το Torque σε ζεύγος δυνάμεων. 

Στα σχολικά βιβλία της εποχής μας, το ζήτημα παρουσιάζει προβλήματα που δεν έχουν λυθεί. Στο εγκεκριμένο για τα αγγλικά σχολεία Physics έκδοση Oxford  η διάκριση ( σελ. 36) είναι εμφανής. Για τη ροπή δύναμης ως προς σημείο χρησιμοποιείται το Moment of a force ενώ για τη ροπή ζεύγους το Torque. Στο Physics έκδοση Collins η διάκριση των όρων παρουσιάζεται ( σελ. 71 ) με σαφήνεια «The combined moment of a couple is called the torque»⁷ . 

Αντίστοιχη διάκριση μπορούμε να επισημάνουμε στην έννοια «στροφορμή (ροπή της ορμής ) ως προς σημείο» και «στροφορμή» χωρίς γεωμετρική αναφορά, χωρίς κάποιο «ως προς». Ένα σύστημα δύο υλικών σημείων με ορμές ίσων μέτρων και αντιπαράλληλες έχει στροφορμή χωρίς αναφορά σε γεωμετρικό σημείο. Είναι μια ροπή του ζεύγους των ορμών. Αυτό ισχύει για μία στρεφόμενη ομογενή σφαίρα περί άξονα διερχόμενο από το κέντρο μάζας.

5. Ροπή και μεταβιβαζόμενη ενέργεια. Έργο ροπής.

Κυρία, κυρία . .... το «έργο ροπής μιας δύναμης» και το «έργο δύναμης» δεν είναι το ίδιο πράγμα ; Και αν είναι έτσι γιατί μαθαίνουμε δύο φράσεις διαφορετικές ;

Και είπε η κυρία : Δεν έχεις άδικο. «Το έργο ροπής μιας δύναμης ως προς σημείο » και το «έργο της συγκεκριμένης δύναμης είναι η ίδια έννοια». Οι φυσικοί χρησιμοποιούν την έννοια «έργο ροπής» αναφερόμενοι σε «ροπή ζεύγους» τη λεγόμενη και απλά ροπή . Η ιδιαιτερότητα της έννοιας «ζεύγος δυνάμεων» και η διάκρισή της από την έννοια «μηδενική συνισταμένη» σχετίζεται και με το ότι «η δράση ενός ζεύγους για οποιοδήποτε dt συνεπάγεται μεταβίβαση ενέργειας» κάτι που δεν συμβαίνει με το «συνισταμένη μηδέν».

Το λεγόμενο «ολικό έργο- αλγεβρικό άθροισμα των έργων » δυνάμεων ασκουμένων στο ίδιο σώμα είναι - σύμφωνα με το γνωστό θεώρημα – ίσο με τη μεταβολή της κινητικής ενέργειας του σώματος. Το ολικό αυτό έργο είναι ίσο και με το έργο της συνισταμένης, υπολογίζεται δηλαδή είτε ως αλγεβρικό άθροισμα των έργων είτε ως έργο της συνισταμένης των ασκουμένων στο σώμα δυνάμεων.

Εάν όμως οι ασκούμενες στο σώμα δυνάμεις ανάγονται σε ζεύγος το ολικό έργο- αλγεβρικό άθροισμα των έργων- δεν μπορεί να είναι έργο της συνισταμένης διότι συνισταμένη δεν υφίσταται.

Στην περίπτωση δηλαδή αυτή το ολικό έργο δεν είναι ίσο με το έργο κάποιας δύναμης και για την περιγραφή του εισάγεται η έννοια «έργο ζεύγους με συγκεκριμένη ροπή » ή «έργο ροπής» και εφόσον η τιμή της ροπής, κατά τη μεταβίβαση ενέργειας, διατηρείται σταθερή αποδεικνύεται ίσο με το γινόμενο «ροπή x γωνιακή μετατόπιση».

Η έννοια έργο είναι πάντα «έργο δύναμης ή έργο δυνάμεων» και η «έργο ροπής μιας δύναμης ως προς σημείο» είναι έννοια περιττή διότι ταυτίζεται με το έργο της συγκεκριμένης δύναμης . Ωστόσο σε περίπτωση που οι ασκούμενες στο σώμα δυνάμεις συνιστούν ζεύγος, οπότε υφίσταται και η έννοια «ροπή» - και όχι ροπή μιας δύναμης ως προς σημείο- χρησιμοποιούμε τον όρο έργο ροπής με τον οποίο υποδηλώνουμε ότι πρόκειται για μεταβιβαζόμενη ενέργεια από δυνάμεις που δεν ανάγονται σε μία δύναμη ούτε στη δύναμη μηδέν.

Στη γενική δηλαδή περίπτωση που οι ασκούμενες δυνάμεις δεν συνιστούν ζεύγος την έννοια έργο ροπής μπορούμε να την αποφεύγουμε. Δεν είναι τίποτα περισσότερο ή τίποτα λιγότερο από την έννοια έργο δύναμης και η διδασκαλία μιας ακόμα έννοιας είναι περιττή, εκτός του ότι στα μάτια των διδασκομένων αυτό μεταφράζεται ότι έχουμε δύο ειδών έργα: έργο δύναμης και ειδικά στη στροφική κίνηση κάποιο «έργο ροπής».

6. Το φαινόμενο ΙΣΟΡΡΟΠΙΑ.

Για ένα μηχανικό στερεό – rigid body- στο οποίο ασκούνται δυνάμεις συνεπίπεδες,

oι αλγεβρικές δομές ΣF_x = 0 και ΣF_y = 0 εξασφαλίζουν τη μηδενική επιτάχυνση του κέντρου μάζας, αλλά η εξίσωση Στ_Α = 0 για ένα τυχαίο σημείο Α εξασφαλίζει το ότι οι δυνάμεις δεν συνιστούν ζεύγος. Αυτό σημαίνει ότι οι τρεις ανεξάρτητες εξισώσεις το αρχικά ακίνητο στερεό θα διατηρηθεί ακίνητο.

Τρεις ανεξάρτητες εξισώσεις οι οποίες επίσης εξασφαλίζουν την ισορροπία είναι οι Στ_Α = 0,

Στ_Β = 0 και Στ_Γ = 0 , αρκεί τα γεωμετρικά σημεία Α, Β και Γ να μην ανήκουν στην ίδια ευθεία. Πράγματι από τις εξισώσεις αυτές συμπεραίνεται α. ότι αποκλείεται η ισοδυναμία με ζεύγος και β. ότι η συνισταμένη είτε είναι μηδέν είτε εάν υπάρχει θα διέρχεται από τα σημεία Α, Β και Γ. Εφόσον όμως τα Α, Β και Γ δεν είναι ανήκουν στην ίδια ευθεία αυτό αποκλείεται και η συνισταμένη θα είναι μηδέν .

7. Το φαινόμενο στροφική κίνηση

Στη δεκαετία που ακολουθεί τον θάνατο του Newton και του Varignon θα εμφανιστεί στο προσκήνιο ο 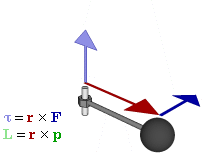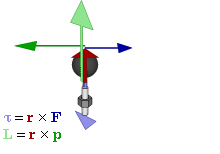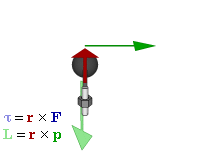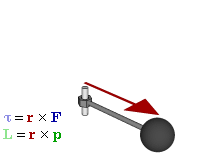Leonhard Euler (Λέοναρντ Όιλερ), ο οποίος θα συνδυάσει την έννοια ροπή δύναμης με τις καινούριες -κέντρο μάζας, ροπή αδράνειας, ροπή της ορμής και γωνιακή επιτάχυνση -και θα οδηγηθεί στη διατύπωση του γενικού νόμου για τη στροφική κίνηση ( λέγεται και 2^ος νόμος του Euler) στον οποίο η έννοια ροπή θα παίξει τον ρόλο που έπαιζε η δύναμη στη δυναμική του υλικού σημείου του Isaac Newton. Η ολική ροπή είναι ίση με τον ρυθμό μεταβολής της στροφορμής τ_ολ = dL/dt

Αν το σώμα είναι αρχικά ακίνητο και η ολική ροπή είναι «ροπή ζεύγους, torque» - χωρίς αναφορά σε σημείο – η στροφορμή δεν αναφέρεται σε σημείο. Η «ροπή» θα είναι ίση με τον ρυθμό μεταβολής της στροφορμής ως προς οποιοδήποτε σημείο.

Η - μέσα από τη διδασκαλία –

οικοδόμηση της έννοιας ΡΟΠΗ

Το πρώτο βήμα. Η ΕΜΠΕΙΡΙΑ

Η εμπειρία μνήμη .

Ερωτήματα προς τους διδασκόμενους ώστε να ανακληθούν «προσωπικές αναμνήσεις» σχετιζόμενες είτε με την παιδική ηλικία και με τραμπάλα της παιδικής χαρά , είτε με στροφικές κινήσεις μοχλών

Η εργαστηριακή εμπειρία . Οριζόντια ομογενής ράβδος, στηριζόμενη σε κατακόρυφο στέλεχος στο μέσον της Ο και στρεπτή περί άξονα κάθετο σε αυτήν και οριζόντιο. Ένα βαρίδι Σ₁ βάρους m₁g κρεμασμένο σε απόσταση d₁ από το Ο, κι ένα άλλο βαρίδι Σ₂ βάρους m₂g από την άλλη πλευρά κρεμασμένο σε απόσταση d₂. Ο διδάσκων συγκρατεί τη ράβδο και ζητεί από τους διδασκόμενους να θεωρήσουν ότι η δύναμη F την οποία ασκεί κάθε βαρίδι στη ράβδο είναι ίση με το βάρος του ( F₁= m₁g = F₁, m₂g = F₂ ) και να προβλέψουν τι θα συμβεί εάν την αφήσει τη ράβδο ελεύθερη σε περίπτωση που d₁ > d₂ και m₁g = m₂g . Κάθε μαθητής καταγράφει τη δική του πρόβλεψη , στη συνέχεια η ράβδος αφήνεται και το πρώτο συμπέρασμα «μολονότι οι ασκούμενες δυνάμεις είναι ίσες η ράβδος στρέφεται προς το μέρος της δύναμης που ασκείται σε μεγαλύτερη απόσταση», ώστε να διαφανεί ότι η τιμή και μόνο της ασκούμενης δύναμης δεν αρκεί για την πρόβλεψη «προς τα που θα γίνει η περιστροφή».

Ο διδάσκων αλλάζει τα βαρίδια και τις αποστάσεις ανάρτησης και καλεί τους μαθητές να προβλέψουν τι θα συμβεί σε περίπτωση που d₂ /d₁ = 2 και F₁/ F₂ = 2 . Ακολουθεί η διαπίστωση ότι η ράβδος διατηρείται ακίνητη και επισημαίνεται ότι αυτό που συμβαίνει είναι «ισορροπία». Η ισότητα d₂ /d₁ = F₁/ F₂ καταγράφεται ως ισότητα δύο γινομένων F₁d₁ = F₂d₂ . Επισημαίνεται ότι η ισότητα αυτή είναι ισότητα δύο ροπών, η μία είναι το γινόμενο F₁d₁ της , η άλλη το γινόμενο F₂d₂ .και ότι μια τέτοια ισότητα ροπών σχετίζεται με το φαινόμενο «ισορροπία».

Επαναλαμβάνεται η εμπειρία με d₂ /d₁ = 1/3 και F₂/ F₁ = 4 , καταγράφονται οι προβλέψεις και διατυπώνεται το συμπέρασμα ότι η ράβδος στρέφεται προς την πλευρά 2 όπου η ροπή της δύναμης είναι μεγαλύτερη.

Το δεύτερο βήμα. Αναφορά στον Αρχιμήδη και στον νόμο του μοχλού . Ο Pierre Varignon και η ιδέα ότι το γινόμενο «δύναμη επί απόσταση του φορέα της από το σημείο» συνιστά το μέτρο της ροπής και με το μέτρο της αυτό μπορούμε να περιγράφουμε την ικανότητα της δύναμης στο να συμβάλλει στην περιστροφή αρχικά ακίνητου στερεού. Η μονάδα 1 Νm και το σύμβολο τ . τ = F.d

Αναφορά στην επόμενη ιδέα ότι προκειμένου να περιγράφει και το «προς τα που θα στραφεί» το αρχικά ακίνητο σώμα πρέπει να παριστάνεται με ένα διάνυσμα κάθετο το επίπεδο δύναμης και σημείου. Σχήμα. Αναφορά στην έννοια αλγεβρική τιμή της ροπής – σε σχέση με άξονα. Επιστροφή στο εμπειρικό δεδομένο και περιγραφή της ισότητας των μέτρων των δύο ροπών με το «το αλγεβρικό άθροισμα των ροπών είναι ίσο με μηδέν»

Το τρίτο βήμα. Ορίζεται η έννοια ολική ροπή, ως προς σημείο Ο, ενός συνόλου δυνάμεων ασκουμένων στο ίδιο σώμα. Το θεώρημα των ροπών.

Το τέταρτο βήμα. Αναζήτηση της συνισταμένης δύο παραλλήλων δυνάμεων ασκουμένων στο ίδιο σώμα με βάση το θεώρημα των ροπών. α. Δυνάμεις με την ίδια κατεύθυνση β. Δυνάμεις με αντίθετες κατευθύνσεις με ειδική αναφορά στην περίπτωση που οι δυνάμεις έχουν ίσα μέτρα.

Η έννοια ζεύγος και η ιδιαιτερότητά της. Η έννοια ροπή ζεύγους και η ιδιαιτερότητά της .

Το κέντρο μάζας ενός σώματος και η εξίσωση F = ma_cm. Εφόσον σε ένα σώμα ασκείται ζεύγος δυνάμεων ισχύει ΣF_x = 0 ΣF_y = 0 άρα το κέντρο μάζας έχει μηδενική επιτάχυνση

Το πέμπτο βήμα. Το φαινόμενο « ισορροπία ενός αρχικά ακίνητου στερεού» υπό την επίδραση συνεπιπέδων δυνάμεων. Εφόσον ένα σώμα ισορροπεί ισχύουν τρεις ανεξάρτητες εξισώσεις ΣF_x = 0 , ΣF_y = 0, Στ_Α= 0 , για οποιοδήποτε σημείο Α. Ισοδύναμα οι εξισώσεις Στ_Α= 0 Στ_Β= 0 Στ_Γ = 0 , με τα γεωμετρικά σημεία Α, Β και Γ να μην ανήκουν στην ίδια ευθεία .

Γενικότερα, εφόσον ένα σώμα κινείται μεταφορικά με σταθερή ταχύτητα ισχύουν οι τρεις ανεξάρτητες εξισώσεις και αντίστροφα.

Το έκτο βήμα. Αν σε ακίνητο σώμα ασκηθούν δύο δυνάμεις που συνιστούν ζεύγος το σώμα θα εκτελέσει στροφική κίνηση με το κέντρο βάρος να διατηρείται ακίνητο.

Το έβδομο βήμα . Ροπή δύναμης ως προς σημείο και «ΡΟΠΗ»

Το όγδοο βήμα . Στροφική κίνηση . Εφόσον ένα σώμα στρέφεται (ή είναι στρεπτό) περί σταθερό άξονα, η συνιστώσα της ολικής ροπής ως προς ένα σημείο Ο του άξονα περιστροφής χαρακτηρίζεται και «ολική ροπή κατά τον άξονα περιστροφής» .

Ένας νόμος για τη στροφική κίνηση . Η ολική ροπή κατά τον άξονα περιστροφής είναι ίση με το γινόμενο «Ροπή αδράνειας ως προς τον άξονα περιστροφής» επί «τη γωνιακή επιτάχυνση του σώματος». Η εξίσωση τ = Ια_γων

Το ένατο βήμα. Ροπή και μεταβολή της στροφορμής. O γενικότερος νόμος για τη στροφική κίνηση. Η εξίσωση τ = dL/dt

Το δέκατο βήμα. Ροπή και μεταβιβαζόμενη ενέργεια. Έργο ροπής.

Παραπομπές

1. Η ροπή μιας δύναμης ως προς Α «συμβάλλει» στο να διαμορφωθεί το «πόσο έντονα» θα στραφεί το σώμα περί άξονα διερχόμενο από το σημείο Α. Το πόσο, δηλαδή. έντονα θα στραφεί το σώμα δεν καθορίζεται μόνο από τη ροπή αλλά και από το πως «κατανέμεται» η μάζα του σώματος σε σχέση με τον άξονα. Αυτό το τελευταίο περιγράφεται με την έννοια ροπή αδράνειας του σώματος ως προς τον συγκεκριμένο άξονα.

2. Το θεώρημα των ροπών. Μια απόδειξη

Θεωρούμε τις ροπές των δυνάμεων F₁ και F₁ ως προς το σημείο Α καθώς

και τη ροπή τ_ολ της συνισταμένης F_ολ ως προς το ίδιο αυτό σημείο

Η ως προς Α ροπή τ₁ της F₁ έχει μέτρο ίσο με το διπλάσιο του εμβαδού (ΟΑΒ) του τριγώνου ΟΑΒ

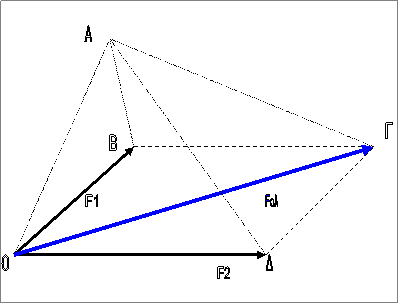Η ως προς Α ροπή τ₂ της F₂ ως προς Α έχει μέτρο ίσο με το διπλάσιο του εμβαδού (ΟΑΔ) του τριγώνου ΟΑΔ

Η ως προς Α ροπή τ_ολ της συνισταμένης F_ολ έχει μέτρο ίσο με το διπλάσιο του εμβαδού (ΟΑΓ) του τριγώνου ΟΑΓ.

Αν είναι Ε το εμβαδόν του παραλληλογράμμου ΟΒΓΔ

(ΟΑΓΔ) = ½ τ₂ + (ΔΑΓ)

(ΟΑΓΔ) = ½ τ_ολ + ½Ε

(ΔΑΓ) = ½ τ₁ + ½Ε

Από τις παραπάνω σχέσεις προκύπτει ότι τ₁ + τ₂ = τ_ολ

3. Η συνισταμένη δύο παραλλήλων δυνάμεων ασκουμένων στο ίδιο σώμα μπορεί να προσδιοριστεί με το θεώρημα των ροπών. Το εφαρμόζουμε επιλέγοντες γεωμετρικό σημείο, ένα σημείο Α από το οποίο ανήκει στον φορέα της συνισταμένης, οπότε τ_ολ = 0 .

Αν οι δυνάμεις F₁ και F₂ απέχουν κατά d και

α. έχουν την ίδια κατεύθυνση υποθέτουμε ότι ο φορέας της συνισταμένης απέχει από τη μία , έστω την F₁, κατά x , οπότε ισχύει

F₁x - F₂(d-x) = 0 x = F₂d/( F₁+ F₂). Το μέτρο της συνισταμένης θα είναι ίσο με F₁+ F₂

β. έχουν αντίθετες κατευθύνσεις υποθέτουμε ότι ο φορέας της συνισταμένης απέχει από τη μεγαλύτερη από αυτές , έστω την F₁, κατά x

οπότε ισχύει F₁x - F₂(d+x) = 0 x = F₂d/( F₁- F₂) .

Παρατηρούμε ότι για να υπάρχει συνισταμένη πρέπει F₁- F₂ ≠0 F₁ ≠ F₂

Πρέπει δηλαδή οι αντιπαράλληλες δυνάμεις να μην συνιστούν ζεύγος .

Εφόσον F₁ ≠ F₂ , το μέτρο της συνισταμένης θα είναι ίσο με F₁- F₂

4. Για να πάρει τη σκυτάλη ο Euler,- Όιλερ- ο οποίος θα εισάγει και την έννοια ροπή της ορμής –τη λεγόμενη στροφορμή. Ο όρος moment θα επικρατήσει στις περισσότερες ευρωπαϊκές γλώσσες, ως moment , αλλά και με τις παραλλαγές momento ( στη γλώσσα των Ιταλών, των Ισπανών και των Πορτογάλων ), drehmoment στα γερμανικά, στη γλώσσα των Ρουμάνων momentul, στα αλβανικά και στα τούρκικα momenti, στα φινλανδική voimamomentti ( ροπή δύναμης) στη γλώσσα των Λιθουανών momentas jėga ( ροπή δύναμης) ..

5. Τι σημαίνει «ΣΥΝΙΣΤΑΜΕΝΗ» δυνάμεων που ασκούνται στο ίδιο σώμα;

Υπάρχει «μία δύναμη που μπορεί να αντικαταστήσει τις δυνάμεις αυτές και να επιφέρει το ίδιο αποτέλεσμα» διαβάζουμε στα σχολικά βιβλία. Βέβαια τα σχετικά βιβλία των πρώτων τάξεων του Λυκείου βασίζονται σε Αναλυτικό Πρόγραμμα αναφερόμενο σε δυναμική υλικού σημείου.

Τι συμβαίνει γενικότερα ;Ποιο είναι αυτό το αποτέλεσμα το οποίο θα προκαλέσει η ΜΙΑ δύναμη αυτή που «μπορεί να αντικαταστήσει» τις δύο ασκούμενες δυνάμεις; Θα προκαλέσει :

Την ίδια επιτάχυνση του κέντρου μάζας; Την ίδια μεταβολή ορμής ;

Την ίδια μεταβολή στροφορμής ;  Την ίδια μεταβίβαση ενέργειας ;

Στην αγγλοσαξωνική βιβλιογραφία – τουλάχιστον σε συγγραφείς που είναι προσεκτικοί –

υπάρχουν δύο έννοιες διαφορετικές . Το Vector sum και η Resultant force.

H μαθηματική έννοια Vector sum είναι το άθροισμα των αντίστοιχων διανυσμάτων. Από πολλούς συγγραφείς για την περίπτωση ασκουμένων στο ίδιο σώμα δυνάμεων λέγεται και Net force. Είναι η μία εκείνη δύναμη εκείνη η οποία, σε συνδυασμό με την αδράνεια του σώματος, θα καθορίζει την επιτάχυνση του κέντρου μάζας   F_net= ma_cm .

Resultant force είναι η δύναμη εκείνη η οποία σε συνδυασμό με την αδράνεια του σώματος θα καθορίσει τη μεταβολή στην συνολική  κινητική κατάσταση.   Αν το αντικείμενο στο οποίο ασκούνται είναι υλικό σημείο οι δύο έννοιες ταυτίζονται .

Τι συμβαίνει γενικότερα ;  Μπορούμε συμβολικά να πούμε ότι : Vector force (Net force) και  η σχετιζόμενη με αυτή torque (ροπή ζεύγους)  = Resultant force

Στην περίπτωση του ζεύγους, η net force είναι μηδενική, αλλά η resultant force δεν είναι μηδενική . Στην ελληνική βιβλιογραφία χρησιμοποιείται και για τις δύο ο όρος «συνισταμένη δυνάμεων». 

6.Το θέμα Α3 των πανελλαδικών εξετάσεων 2014 φώτισε ένα εννοιολογικό πρόβλημα. Είναι δεκάδες οι φυσικοί που χρησιμοποίησαν τη  σχεδόν εδραιωμένη λογική: «Εφόσον η κίνηση είναι μεταφορική δεν μπορεί να υπάρχει ροπή». Για τη δική μας οπτική πίσω από το πρόβλημα ελλοχεύει η ταύτιση της έννοιας «ροπή δύναμης ως προς σημείο» και της - χωρίς γεωμετρική αναφορά -έννοιας «ροπή». Το ζήτημα σχετίζεται και με την υποβαθμισμένη από το Αναλυτικό Πρόγραμμα διδασκαλία της ιδιαιτερότητας έννοιας «Ζεύγος δυνάμεων» η οποία στο σχολικό βιβλίο παρουσιάζεται έτσι ώστε να μην φωτίζεται καθόλου μα καθόλου η ιδιαιτερότητά της.

7. Ωστόσο στο ανταγωνιστικό Physics έκδοση Cambridge ( σελ. 152 ) οι δύο όροι θεωρούνται συνώνυμα