Ανδρέας Ιωάννου Κασσέτας

Το βιβλίο της φύσης είναι γραμμένο στη γλώσσα των μαθηματικών

Galileo Galilei

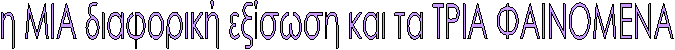
H διαφορική εξίσωση

dx/dt + ax = 0

λύση της είναι η συνάρτηση x = x₀e^-at

Τα ΦΑΙΝΟΜΕΝΑ

1. Ραδιενέργεια

Το εμπειρικό δεδομένο dN/dt = - λΝ

N = N₀e^-λt

2. Εκφόρτιση πυκνωτή

Ο κανόνας του Kitchhoff IR + q/C =0 Rdq/dt + q/C = 0

dq/dt + q/CR = 0 q = q₀e^-λt/RC

3. Άνοιγμα κυκλώματος R, L

Ο δεύτερος κανόνας του Kitchhoff IR + LdI/dt = 0

dI/dt + R/LI = 0 I = I₀e^-Rt/L

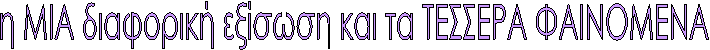
H διαφορική εξίσωση

dx/dt + ax = β

λύση της είναι η συνάρτηση x = x_ορ(1-e ^-at) x_ορ= β/α

Τα ΦΑΙΝΟΜΕΝΑ

1. Πτώση στον αέρα

Ο δεύτερος νευτωνικός νόμος της κίνησης

mg – F_αντ = ma mg – bυ = mdυ/dt dυ/dt + b/m υ = g

υ = υ_ορ ( 1 – e^–bt/m )

2. Κίνηση ρευματοφόρου αγωγού σε μαγνητικό πεδίο

Ο δεύτερος νευτωνικός νόμος της κίνησης

mg – F_L = ma F_L = ΒΙL = B²L²υ/R = b υ όπου b = B²L²/R

mg – bυ = mdυ/dt dυ/dt + b/m υ = g

υ = υ_ορ ( 1 – e^–bt/m )

3. Φόρτιση πυκνωτή

Ο δεύτερος κανόνας του Kirchhoff IR + q/C = E Rdq/dt + q/C = E dq/dt + q/CR = E

q = E C ( 1- e^-λt/RC)

4. Αποκατάσταση ρεύματος σε κύκλωμα R, L

Ο δεύτερος κανόνας του Kitchhoff IR + LdI/dt = Ε dI/dt + R/LI = Ε

I = E/R ( 1 - e^-Rt/L )

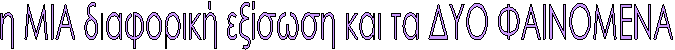
H διαφορική εξίσωση

d²x/dt²+ ax = 0

λύση της η συνάρτηση x=x₀ημ(Öαt+φ)

Τα ΦΑΙΝΟΜΕΝΑ

1. Μηχανική αρμονική ταλάντωση, αμείωτη

Ο δεύτερος νευτωνικός νόμος της κίνησης

– Dx = ma – Dx = md²x/dt²

ẍ +D/m x = 0 x=x₀ημωt

( αποδεχόμενοι ότι για t = 0 ισχύει x= 0 και υ > 0 ) ω= ÖD/m Τ= 2π Öm/D

2. Ηλεκτρομαγνητική αρμονική ταλάντωση,αμείωτη

Ο δεύτερος κανόνας του Kitchhoff LdI/dt + q/C = 0 d²q/dt² + 1/_LC q = 0

q=q₀ημωt

( αποδεχόμενοι ότι για t = 0 ισχύει q = 0 και I > 0 ) ω= 1/_ÖLC Τ= 2π ÖLC

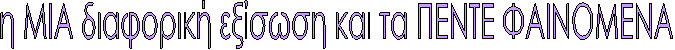
H διαφορική εξίσωση

d²x/dt²+ αdx/dt +βx = 0

εάν α² -4β>0 λύση η συνάρτηση x=c₁e^ρ1t-c₂e^ρ2t

εάν α² -4β<0 λύση η συνάρτηση x=ce^AtημΒt

Τα ΦΑΙΝΟΜΕΝΑ

Φθίνουσα μηχανική ταλάντωση

Ο δεύτερος νευτωνικός νόμος της κίνησης

-b υ –Dx = ma -b dx/dt – Dx = md²x/dt²

d²x/dt² + b/_m dx/dt + D/_m x = 0

1. Με ισχυρή απόδοση

b² > 4 Dm x=ce^ρ1t-ce^ρ2t t = 0 x= 0

Τα ρ₁ και ρ₂ λύσεις της Υ²+by/m + D/m = 0

2. Με ασθενή απόδοση

b² < 4 Dm x=ce^AtημΒt t = 0 x= 0 c = υ_αρχ/Β

A+Bi = ρ₁ Α-Bi = ρ₂ , όπου ρ₁ ρ₂ οι μιγαδικές ρίζες της Υ²+by/m + D/m = 0

Φθίνουσα ηλεκτρομαγνητική ταλάντωση

Ο δεύτερος κανόνας του Kitchhoff LdI/dt + q/C +IR = 0

Παραγωγίζοντας ως προς τον χρόνο d²I/dt² +R/L dI/dt +1/_CL I= 0

3. Με ισχυρή απόδοση

R² > 4L/C I=ce^ρ1t-ce^ρ2t t = 0 x= 0

Τα ρ₁ και ρ₂ λύσεις της Υ²+by/m + D/m = 0

4. Με ασθενή απόδοση

R² < 4L/C I=ce^AtημΒt c = (dI/dt)_αρχ/Β

A+Bi = ρ₁ Α-Bi = ρ₂ , όπου ρ₁ και ρ₂ οι μιγαδικές ρίζες της Υ²+Ry/L + 1/_CL = 0

5. Ηλεκτρικό ρεύμα σε R, L, C σε σειρά με σταθερή τάση

IR + LdI/dt +q/C = E Παραγωγίζουμε ως προς χρόνο

d²I/dt² +R/L dI/dt +1/_CL I= 0

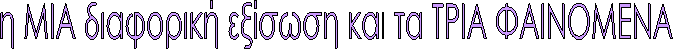
H διαφορική εξίσωση

d²x/dt²+ αdx/dt +βx = γημωt

Τα ΦΑΙΝΟΜΕΝΑ

1. Εξαναγκασμένη μηχανική ταλάντωση

Ο δεύτερος νευτωνικός νόμος της κίνησης

F₀ημωt-bυ –Dx = ma

d²x/dt² +b/_m dx/dt + D/_m x = F₀ημωt

x = c₁e^ρ1t + c₂e^ρ2t +c₃ημωt +c₄συνωt

2. Εξαναγκασμένη ηλεκτρομαγνητική ταλάντωση

Ο δεύτερος κανόνας του Kitchhoff LdI/dt + q/C +IR = V₀ημωt

Παραγωγίζουμε ως προς t.

d²I/dt² + R/L dI/dt + 1/_CL I= ωV₀συνωt

3. Εναλλασόμενο ρεύμα σε κύκλωμα R, L, C, σε σειρά

Ο δεύτερος κανόνας του Kitchhoff LdI/dt + q/C +IR = V₀ημωt

Παραγωγίζουμε ως προς t.

d²I/dt² + R/L dI/dt + 1/_CL I= ωV₀συνωt