Ανδρέας Ιωάννου Κασσέτας

 

το φαινόμενο ΣΤΡΟΦΙΚΗ ΤΑΛΑΝΤΩΣΗ
 

 

 

 

 


Η στροφική ταλάντωση είναι στροφική κίνηση ενός rigid body κατά την οποία μεταβάλλεται η φορά της περιστροφής και εκδηλώνεται περιοδικότητα.

Τέτοια κίνηση κάνει η μαγνητική βελόνα σε ομογενές μαγνητικό πεδίο και ένα ηλεκτρικό δίπολο σε ομογενές ηλεκτρικό πεδίο

Σε κάθε στροφική ταλάντωση υπάρχει μια θέση ισορροπίας στην οποία όταν βρεθεί ο ταλαντωτής θα έχει την ελάχιστη δυναμική ενέργεια.

Κατά την εξέλιξη της κίνησης εκδηλώνεται ΡΟΠΗ ΕΠΑΝΑΦΟΡΑΣ. 

Αν σε μία στροφική ταλάντωση η  ΡΟΠΗ ΕΠΑΝΑΦΟΡΑΣ είναι ανάλογη με τη γωνιακή θέση θ

η στροφική ταλάντωση είναι αρμονική.             τ = - Dθ

Σύμφωνα με τον δεύτερο νόμο της κίνησης       τ = Ιαγων         τ = Ιd2θ/dt2 .

                               Ιd2θ/dt2   = - Dθ        

      Η λύση της διαφορικής εξίσωσης  δίνει  θ = θ0ημ ( ωt +φ ) με ω = √D/I

Αν για τη γωνιακή θέση είναι ισχύει θ = θ0ημ( ωt +φ )  η στροφική ταλάντωση είναι αρμονική.

 η γωνιακή θέση                                 θ = θ0ημ( ωt +φ )

η γωνιακή ταχύτητα                    dθ/dt = ωθ0συν(ωt + φ)

η γωνιακή επιτάχυνση           d2θ/dt2   = - ω2θ0ημ(ωt +φ) = - ω2θ

η ΡΟΠΗ ΕΠΑΝΑΦΟΡΑΣ        τ = - Ιω2θ    Ιω2 = D     T = 2π √Ι/D

                                   

Το φυσικό εκκρεμές

Κάθε σώμα που βρίσκεται σε πεδίο βαρύτητας και «κρέμεται» είναι ένα φυσικό εκκρεμές.

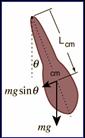« Κρέμεται» σημαίνει ότι το κέντρο μάζας του είναι χαμηλότερα από το σημείο ανάρτησης, η ισορροπία του δηλαδή είναι ευσταθής. 

 

Αν ενεργοποιηθεί κατάλληλα και αφεθεί θα εκτελέσει στροφική ταλάντωση

Αν ενεργοποιηθεί έτσι ώστε η αιώρησή του να περιορίζεται

σε μικρές γωνιακές μετατοπίσεις,  έτσι ώστε ημθ = θ,   

η κίνησή του θα είναι στροφική αρμονική ταλάντωση

      Σε μια τυχαία στιγμή της αιώρησης τ = - mgημθ. L άρα,  για μικρές γωνίες,  τ = - - mgLθ

Άρα η κίνηση είναι στροφική αρμονική ταλάντωση με D = mgL,

όπου L η απόσταση του σημείου ανάρτησης από το κεντρο μάζας

Για την περίοδο Τ ισχύει         Τ = 2π√Ι/mgL

όπου  Ι η ροπή αδράνειας ως τον προς οριζόντιο άξονα αιώρησης

 

 

Η στροφική ταλάντωση της μαγνητικής βελόνας

Όταν ο άξονος της είναι παράλληλος  με τις δυναμικές γραμμές με τον βόρειο πόλο προς τη φορά των δυναμικών η βελόνα ισορροπεί και βρίσκεται σε ευσταθή ισορροπία

Σε μια τυχαία θέση   τ = - F .d     τ = - Bmℓημθ

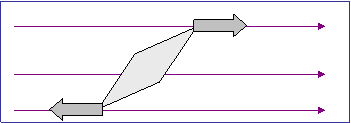Για μικρές γωνίες θ ημθ = θ άρα

              τ = - B m ℓθ συνεπώς η κίνηση

είναι στροφική αρμονική ταλάντωση με

        D = B m ℓ και με περίοδο

                 Τ = 2π√Ι/Bmℓ

 

 

 

 

                       

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Θερμοδυναμική