Φυσική Κατεύθυνσης 2006

ΘΕΜΑ 1^Ο

1. Στο κύκλωμα των εξαναγκασμένων ηλεκτρικών ταλαντώσεων

α. το πλάτος Ι της έντασης του ρεύματος είναι ανεξάρτητο της συχνότητας της εναλλασσόμενης τάσης

β. η συχνότητα της ηλεκτρικής ταλάντωσης του κυκλώματος είναι ανεξάρτητη της χωρητικότητας C του πυκνωτή

γ. η ιδιοσυχνότητα του κυκλώματος είναι ανεξάρτητη της χωρητικότητας του πυκνωτή

δ. όταν η συχνότητα της εναλλασσόμενης τάσης γίνει ίση με την ιδιοσυχνότητα του κυκλώματος, έχουμε μεταφορά ενέργειας στο κύκλωμα κατά το βέλτιστο τρόπο

2 . Μονοχρωματική ακτίνα φωτός προσπίπτει πλάγια στη διαχωριστική επιφάνεια δύο οπτικών μέσων 1 και 2 . Οι δείκτες διάθλασης στα μέσα 1 και 2 είναι αντίστοιχα n₁ και n₂ με n1> n2. Αν η μονοχρωματική ακτίνα ανακλάται ολικά

α . υπάρχει διαθλώμενη ακτίνα

β. η γωνία πρόσπτωσης είναι ίση με τη γωνία ανάκλασης

γ. η γωνία πρόσπτωσης είναι μικρότερη από τη γωνία ανάκλασης

δ. η ταχύτητα διάδοσής της μεταβάλλεται

3. Σ’ ένα στάσιμο κύμα όλα τα μόρια του ελαστικού μέσου στο οποίο δημιουργείται

α . έχουν ίδιες κατά μέτρο ταχύτητες

β. έχουν ίσα πλάτη ταλάντωσης

γ. διέρχονται ταυτόχρονα από τη θέση ισορροπίας

δ. έχουν την ίδια φάση

Εδώ διαβάζουμε ότι «ταλαντώνονται τα ΜΟΡΙΑ»

4. Κατά τη σύνθεση δύο απλών αρμονικών ταλαντώσεων ίδια διεύθυνσης, που γίνονται γύρω από το ίδιο σημείο, με το ίδιο πλάτος Α και συχνότητες f₁ και f₂ που διαφέρουν λίγο μεταξύ τους

α. το μέγιστο πλάτος της ταλάντωσης είναι 2Α .

β. όλα τα σημεία ταλαντώνονται με το ίδιο πλάτος

γ. ο χρόνος ανάμεσα σε δύο διαδοχικούς μηδενισμούς του πλάτους είναι Τ= 1/( f₁+ f₂)

δ. ο χρόνος ανάμεσα δύο διαδοχικούς μηδενισμούς του πλάτους είναι Τ = 1/2|f₁- f₂|

Εδώ διαβάζουμε ότι «ταλαντώνονται τα ΣΗΜΕΙΑ»

Τι είναι αυτό που ταλαντώνεται και συγχρόνως έχει ενέργεια;

Μόριο, γεωμετρικό σημείο ή κάτι άλλο ;

Μάλλον κάποιοι έχουν μεταφράσει το PARTICLES με δικό τους τρόπο.

Ανδρέας Ιωάννου Κασσέτας

5. α. Το φαινόμενο Doppler χρησιμοποιείται από τους γιατρούς, για να παρακολουθήσουν την ροή του αίματος Σωστό

β. Στις ανελαστικές κρούσεις δεν διατηρείται η ορμή

γ. Σύμφωνα με την Αρχή της επαλληλίας, η συνεισφορά κάθε κύματος στην απομάκρυνση κάποιου σημείου του μέσου εξαρτάται από την ύπαρξη του άλλου κύματος

δ. Όταν μονοχρωματικό φως διέρχεται από ένα μέσο σε κάποιο άλλο με δείκτες διάθλασης n₁ # n₂, το μήκος κύματος της ακτινοβολίας είναι το ίδιο στα δυο μέσα

ε. Η σταθερά απόσβεσης b σε μία φθίνουσα ταλάντωση εξαρτάται από της ιδιότητες του μέσου Σωστό

Σχόλιο. Το 5α είναι κατά τη δική μας εκτίμηση εξεζητημένο.

Η επιλογή του θέτει εκ των πραγμάτων το ερώτημα:

« Τι ακριβώς θέλουμε να αξιολογήσουμε ; »

ΘΕΜΑ 2^Ο

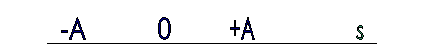1. Σε σημείο ευθείας ε βρίσκεται ακίνητη ηχητική πηγή S που εκπέμπει ήχο σταθερής συχνότητας. Πάνω στην ίδια ευθεία ε παρατηρητής κινείται εκτελώντας αρμονική ταλάντωση πλάτους Α, όπως φαίνεται στο σχήμα

Η συχνότητα του ήχου που αντιλαμβάνεται ο παρατηρητής θα είναι μέγιστη όταν αυτός βρίσκεται

α . στη θέση ισορροπίας Ο της ταλάντωσης κινούμενος προς την πηγή

β. στην τυχαία θέση της ταλάντωσής του απομακρυνόμενος από την πηγή

γ. σε μία από τις ακραίες θέσεις της απλής αρμονικής ταλάντωσης μονάδες 2

Να αιτιολογήσετε την απάντησή σας μονάδες 4

O ακροατής ακούει ήχο με συχνότητα μεγαλύτερη από τη συχνότητα της πηγής όταν η μεταξύ τους απόσταση μειώνεται. Καθώς πλησιάζει την πηγή ισχύει f_α = f_s {c_ηχ + |υ_α|} / c_ηχ

Αν τη σχέση αυτή τη δούμε ως συνάρτηση f = σ(|υ_α|) καταλήγουμε στην επιλογή α.

2. Στο ιδανικό κύκλωμα LC του σχήματος έχουμε αρχικά τους διακόπτες Δ₁ και Δ₂ ανοικτούς

Ο πυκνωτής χωρητικότητας έχει φορτιστεί μέσω πηγής συνεχούς τάσης με φορτίο Q₁. Τη χρονική στιγμή t₀ = 0 ο διακόπτης Δ₁ κλείνει, οπότε το κύκλωμα LC₁ εκτελεί αμείωτη ηλεκτρική ταλάντωση. Τη χρονική στιγμή t₁ = 5T/4, όπου Τ η περίοδος της ταλάντωσης του κυκλώματος LC₁, ο διακόπτης Δ₁ ανοίγει και ταυτόχρονα κλείνει ο Δ₂. Το μέγιστο φορτίο Q₂ που θα αποκτήσει ο πυκνωτής χωρητικότητας C₂ όπου C₂ = 4 C₁ , κατά τη διάρκεια της ηλεκτρικής ταλάντωσης του κυκλώματος LC₂ θα είναι ίσο με

α. Q β. Q₁/2 γ. 2Q₁ . μονάδες 2

Να αιτιολογήσετε την απάντησή σας μονάδες 4

To ένα ΦΑΙΝΟΜΕΝΟ είναι η ηλεκτρική ταλάντωση στο κύκλωμα με τον πυκνωτή C₁

To άλλο ΦΑΙΝΟΜΕΝΟ είναι η ηλεκτρική ταλάντωση στο άλλο κύκλωμα με τον πυκνωτή C₂.

Και τα δύο κυκλώματα είναι ιδανικά, άρα μπορούμε να βασιστούμε στον ΝΟΜΟ « Διατήρηση της ενέργειας »

Τη χρονική στιγμή t₁ = 5T/4 που κλείνουμε τον διακόπτη Δ₁ και ανοίγουμε τον Δ₂ το φορτίο του πυκνωτή C₁ είναι μηδενικό και η ενέργεια του μαγνητικού πεδίου ίση με τη μέγιστη ενέργεια του ηλεκτρικού πεδίου, ίση δηλαδή με Q₁²/C₁. Με το ταυτόχρονο άνοιγμα του διακόπτη Δ₂ η ενέργεια του δεύτερου κυκλώματος θα είναι η ενέργεια η αποταμιευμένη στο μαγνητικό πεδίο του πηνίου ίση με Q₁²/C₁ . και θα ΔΙΑΤΗΡΕΙΤΑΙ ποσοτικά αναλλοίωτη.

Τη στιγμή που ο πυκνωτής C₂ αποκτά μέγιστο φορτίο ΟΛΗ η ενέργεια του κυκλώματος είναι αποταμιευμένη στο ηλεκτρικό πεδίο του πυκνωτή και είναι ίση με Q₂²/C₂.

Σύμφωνα με τη Διατήρηση της ενέργειας Q₂²/C₂.= Q₁²/C₁ άρα Q₂ = 2Q₁

Σχόλιο. Το θέμα συνιστά αρκετά σκληρό για 2^ο ΘΕΜΑ. Δύο ΦΑΙΝΟΜΕΝΑ καθόλου απλά, έννοιες όπως η ενέργεια η αποταμιευμένη στο μαγνητικό πεδίο του πηνίου και η ενέργεια η αποταμιευμένη στο ηλεκτρικό πεδίο του πυκνωτή και η απαίτηση να καταφύγει ο εξεταζόμενος σε διπλή ΕΦΑΡΜΟΓΗ στον ΝΟΜΟ Διατήρηση της ενέργειας. Υπερβολικές απαιτήσεις για 2^Ο θέμα. Αναπόφευκτα έρχονται στο μυαλό μας οι χιλιάδες απελπισμένοι που περιμένουν το πρώτο και το δεύτερο θέμα να σέβονται τη νομοθεσία η οποία περιγράφει το επίπεδο του 2^ου θέματος .

3. Κατά μήκος της ευθείας x΄x βρίσκονται στις θέσεις Κ και Λ δύο σημειακές πηγές Π₁ και Π₂ παραγωγής μηχανικών αρμονικών κυμάτων. Η εξίσωση που περιγράφει τις απομακρύνσεις τους από τη θέση ισορροπίας τους σε συνάρτηση με τον χρόνο είναι y = Aημωt. Η απόσταση ΚΛ είναι 6 cm. Το μήκος κύματος των παραγόμενων κυμάτων είναι 4 cm. Σε σημείο Σ της ευθείας x΄x, το οποίο δεν ανήκει στο ευθύγραμμο τμήμα ΚΛ και δεν βρίσκεται κοντά στις πηγές, το πλάτος ταλάντωσής του Α΄ θα είναι

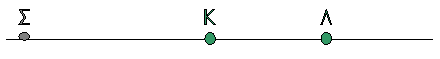
α. Α΄= 2Α β. Α΄= 0 γ. 0 < Α΄ < 2Α μονάδες 2

Να αιτιολογήσετε την απάντησή σας μονάδες 4

Η διαφορά των αποστάσεων του υλικού σημείου Σ από τις δύο πηγές είναι 6cm. Εφόσον το μήκος κύματος είναι 4 cm και το μισό μήκος κύματος 2 cm , διαφορά των αποστάσεων είναι 3λ/2

4. Σε οριζόντιο επίπεδο ο δίσκος του σχήματος με ακτίνα R κυλίεται χωρίς να ολισθαίνει και η ταχύτητα του κέντρου μάζας του είναι υ_cm .

.

Η ταχύτητα του σημείου που βρίσκεται στη θέση Β της κατακόρυφης διαμέτρου και απέχει απόσταση R/2 από το Κ θα είναι

α . 3/2 υ_cm β. 2/3 υ_cm γ. 5/2 υ_cm .

μονάδες 2

Να αιτιολογήσετε την απάντησή σας μονάδες 4

Στο ΦΑΙΝΟΜΕΝΟ κύλιση χωρίς ολίσθηση η ταχύτητα του σημείου επαφής με το έδαφος είναι μηδενική

Η κύλιση αναλύεται σε μεταφορική κίνηση με την ταχύτητα του κέντρου μάζας και σε στροφική περί άξονα που περνάει από το κέντρο μάζας. Λόγω της μεταφορικής κίνησης η ταχύτητα του σημείου Β θα είναι υ_cm, ενώ λόγω της στροφικής περί άξονα κάθετο στο σχήμα που περνάει από το κέντρο μάζας, το Β έχει ταχύτητα ωR/2 , οριζόντια και με την κατεύθυνση της υ_cm. Εφόσον το σημείο επαφής με το έδαφος έχει μηδενική ταχύτητα συνάγεται ότι

υ_cm = ωR. Άρα η ταχύτητα του Β διανυσματικό άθροισμα των δύο ταχυτήτων θα είναι οριζόντια και ίση με 3/2 υ_cm

Άλλη αιτιολόγηση

Η κύλιση μπορεί να θεωρηθεί και «στιγμιαία περιστροφή περί άξονα που περνάει από το κατώτερο σημείο επαφής με το έδαφος» . Για το κέντρο μάζας ισχύει υ_cm. = ω R, όπου ω η στιγμιαία γωνιακή ταχύτητα.

Για το σημείο Β ισχύει υ_Β = ω 3R/2. Άρα υ_Β = 3υ_cm /2

Σχόλιο. Η αιτιολόγηση - κατά τη δική μας εκτίμηση - δεν είναι καθόλου απλή. Εκτός εάν οι υπεύθυνοι της συγκεκριμένης επιλογής ζητούν από τους εξεταζόμενους να γράφουν διάφορους «τύπους» χωρίς να αποσαφηνίζουν «τι παριστάνει το κάθε σύμβολο».

Το δεύτερο θέμα στο σύνολό του κρίνεται βαρύ

ΘΕΜΑ 3^Ο.

Τα σώματα Σ₁ ΚΑΙ Σ₂ αμελητέων διαστάσεων, με μάζες m₁ = 1 kg και m₂ = 3 kg αντίστοιχα

είναι τοποθετημένες σε λείο οριζόντιο επίπεδο. Το σώμα Σ₂ είναι δεμένο στη μία άκρη ιδανικού ελατηρίου σταθεράς k = 100 N/m . Η άλλη άκρη του ελατηρίου είναι ακλόνητα στερεωμένη.

Το ελατήριο με τη βοήθεια νήματος είναι συσπειρωμένο κατά 0,2 m , όπως φαίνεται στο σχήμα.

Τ ο Σ₂ ισορροπεί στο οριζόντιο επίπεδο στη θέση που αντιστοιχεί στο φυσικό μήκος ℓ₀ του ελατηρίου

Κάποια χρονική στιγμή κόβουμε το νήμα και το σώμα Σ₁ κινούμενο προς τα δεξιά συγκρούεται κεντρικά και ελαστικά με το σώμα Σ₂ . Θεωρώντας ως αρχή μέτρησης των χρόνων τη στιγμή της κρούσης και ως θετική φορά κίνησης την προς τα δεξιά, να υπολογίσετε

α. την ταχύτητα του σώματος Σ₁ λίγο πριν την κρούση με το σώμα Σ₂ . μονάδες 6

η λύση

Το ΦΑΙΝΟΜΕΝΟ είναι αρμονική ταλάντωση του Σ₁ πριν από τη σύγκρουση

Είναι μια κίνηση κατά την οποία η ενέργεια διατηρείται

Εφαρμόζουμε τον ΝΟΜΟ «Διατήρηση της ενέργειας»

Επιλέγουμε δύο κατάλληλες χρονικές στιγμές και συμβολίζουμε την αρχική συσπείρωση των 0,2 m με x και

0 + ½ kx² = ½ m₁ υ₁² |υ₁| = 2 m/s Η κατεύθυνσή της είναι βέβαια προς τα δεξιά

β. τις ταχύτητες των σωμάτων Σ₁ και Σ₂, μετά την κρούση μονάδες 6

η λύση

Το ΦΑΙΝΟΜΕΝΟ είναι ελαστική κρούση των δύο σωμάτων

Εφαρμόζουμε τους ΝΟΜΟΥΣ

Διατήρηση της ορμής του συστήματος «Σ₁, Σ₂»

Διατήρηση της ενέργειας του συστήματος «Σ₁, Σ₂ »

Συμβολίζουμε με υ₁ , υ₂ και V₁ , V₂ τις αλγεβρικές τιμές των ταχυτήτων των δύο σωμάτων πριν και μετά

την κρούση αντίστοιχα

m₁ u₁ = m₁V₁ +m₂V₂

½m₁ u₁² = ½m₁V₁² +½m₂V₂²

h η λύση του συστήματος δίνει V₁ = -½υ₁ και V₂ = ½υ₁

Αν θεωρήσουμε άξονα με τέτοιο προσανατολισμό ώστε υ₁ > 0 θα είναι

V₁ = - 1 m/s και V₂ = 1 m/s

γ. την απομάκρυνση του σώματος Σ₁, μετά την κρούση, σε συνάρτηση με τον χρόνο μονάδες 6

η λύση

Το ΦΑΙΝΟΜΕΝΟ είναι η αρμονική ταλάντωση του Σ₁ μετά τη σύγκρουση μια κίνηση κατά την οποία η ενέργεια διατηρείται. Μετά την κρούση το Σ₁ εκτελεί αρμονική ταλάντωση με λιγότερη ενέργεια σε σχέση με την αντίστοιχη κίνησή του πριν από την κρούση . Εφαρμόζουμε τον ΝΟΜΟ «Διατήρηση της ενέργειας»

Τη στιγμή που έχει ταχύτητα V₁ = - 1 m/s το ελατήριο βρίσκεται στο φυσικό του μήκος άρα τι Σ₁ βρίσκεται στη

θέση ισορροπίας . Αν είναι Α το πλάτος της ταλάντωσης

½ m₁ V₁² + 0 = 0 + ½ kΑ²

Άρα το πλάτος Α είναι 0,1 m

Εφόσον η σταθερά της ταλάντωσης είναι ίση με τη σταθερά του ελατηρίου

k = m₁ω² άρα ω = 10 rad/s

Οι συναρτήσεις θέσεις- χρόνου και ταχύτητας - χρόνου είναι

x = Aημ ( ωt + φ ) και υ = υ_maxσυν ( ωt + φ )

Κατά τη χρονική στιγμή που θεωρείται « αρχή χρόνων» ο ταλαντωτής βρίσκεται στη θέση ισορροπίας

( x_a = 0 ) με αρνητική ταχύτητα ( υ = - υ_max < 0 )

Άρα x_α = Aημ φ άρα ημφ = 0 και υ = υ_maxσυνφ άρα συνφ = -1 άρα φ = π

x = 0,1ημ( 10 t + π) ( S.I.)

δ. την απόσταση μεταξύ των σωμάτων Σ₁ και Σ₂, όταν το Σ₁ ακινητοποιείται στιγμιαία για δεύτερη φορά

Δεχθείτε την κίνηση του σώματος Σ₁, τόσο πριν όσο και μετά την κρούση ως απλή αρμονική ταλάντωση σταθεράς k

η λύση

Το ένα ΦΑΙΝΟΜΕΝΟ είναι η ΚΙΝΗΣΗ του Σ₁ μετά την κρούση, η αρμονική ταλάντωση

με ω = 10 rad/s, άρα με περίοδο 2π/10 s. Η ταχύτητα του Σ₁ θα μηδενιστεί για πρώτη φορά τη χρονική στιγμή Τ/4 και μετά για δεύτερη φορά τη χρονική στιγμή 3Τ/4 = 3π/20 s. Tη στιγμή εκείνη ο ταλαντωτής θα βρίσκεται στο άκρο της ταλάντωσης σε απόσταση 0,1 m από τη θέση ισορροπίας προς τα δεξιά.

Το άλλο ΦΑΙΝΟΜΕΝΟ είναι η ΚΙΝΗΣΗ του Σ₂ μετά την κρούση. Είναι μια κίνηση σε οριζόντιο έδαφος χωρίς τριβή άρα μια κίνηση ευθύγραμμη ομαλή

Η απόσταση του από το σημείο της σύγκρουσης θα είναι ίση με το γινόμενο V₂t. Άρα, κινούμενο με V₂= 1m/s το Σ₂ τη χρονική στιγμή 3π/20 s θα απέχει από το σημείο σύγκρουσης 3π/20 m.

Τα δύο σώματα θα απέχουν 0,37 m.

Σχόλιο. Κατά τη δική μας εκτίμηση η διόρθωση των γραπτών θα αποκαλύψει την ΕΛΛΕΙΨΗ «ΚΟΥΛΤΟΥΡΑΣ» στα ζητήματα ΑΛΓΕΒΡΙΚΕΣ ΤΙΜΕΣ και στην έννοια ΣΥΣΤΗΜΑ ΑΝΑΦΟΡΑΣ . Και « αυτό» συμβαίνει τόσο στα ένα και μοναδικό σχολικό βιβλίο όσο και στη διδακτική μας παράδοση.

Το έχουν επισημάνει αρκετοί εκπαιδευτικοί της Δευτεροβάθμιας – όπως ο Ανδρέας Βαλαδάκης – οι οποίοι ερευνούν λίγο περισσότερο τα ζητήματα της διδασκαλίας της Φυσικής.

Ακόμα και η διατύπωση θετική φορά κίνησης την προς τα δεξιά προδίδει την αμηχανία στο χρησιμοποιηθούν τα παραπάνω γνωστικά αντικείμενα.

Θεωρούμε εύστοχη την παρατήρηση συναδέλφων φυσικών οι οποίοι εκτιμούν ότι στο ερώτημα δ του θέματος 3,

η πρόταση «όταν το Σ₁ ακινητοποιείται στιγμιαία για δεύτερη φορά» όφειλε να αντικατασταθεί με την « τη στιγμή που η ταχύτητα του Σ₁ μηδενίζεται για δεύτερη φορά μετά την κρούση» .

Σίγουρα κάποιοι από τους εξεταζόμενους θα νομίσουν ότι η πρώτη φορά που το Σ₁ ακινητοποιείται στιγμιαία είναι στη διάρκεια της κρούσης. Ας μην ξεχνάμε ότι οι άνθρωποι μαθητές στους οποίους απευθυνόμαστε είναι ΔΕΚΑΔΕΣ ΧΙΛΙΑΔΕΣ.

Αλλά και η χρήση του ρήματος ΑΚΙΝΗΤΟΠΟΙΕΙΤΑΙ δεν είναι δόκιμη και όχι μόνο δεν σώζεται από τον επιρρηματικό προσδιορισμό «στιγμιαία» αλλά και αντιφάσκει με αυτόν. Η χρήση του ρήματος ακινητοποιείται δεν πρόκειται να προκαλέσει σύγχυση στους μαθητές αλλά στην γλώσσα μας το σημαινόμενο του «ακινητοποίηση» είναι αυτό που λένε οι φυσικοί «μηδενική ταχύτητα και μηδενική επιτάχυνση» .

Τίποτα δεν «ακινητοποιείται στιγμιαία» .

Το εκκρεμές κατά τη στιγμή που φθάνει στο άκρο της αιώρησης δεν «ακινητοποιείται». Όταν εκτοξεύουμε ένα αντικείμενο προς τα πάνω και φθάσει στο ανώτερο σημείο ΔΕΝ ακινητοποιείται.

Προτείνουμε για το μέλλον είτε το «μηδενίζεται στιγμιαία η ταχύτητα» είτε το «σταματάει για μια στιγμή» .

Κατά τη δική μας πάντα εκτίμηση πρόκειται για ένα θέμα με το οποίο μπορεί να αξιολογηθεί «εάν έχει γίνει κατανοητό το φαινόμενο αρμονική ταλάντωση» μόνο που έχει εμφανώς τα χαρακτηριστικά ΠΡΟΒΛΗΜΑΤΟΣ, ενώ το 3^ο θέμα όφειλε να είναι ΑΣΚΗΣΗ

ΘΕΜΑ 4⁰ .

Άκαμπτη ομογενής ράβδος ΑΓ με μήκος ℓ και μάζα Μ= 3 kg έχει το άκρο της αρθρωμένο και ισορροπεί οριζόντια. Στο άλλο άκρο Γ ασκείται σταθερή κατακόρυφη δύναμη μέτρου 9N με φορά προς τα κάτω. Η ράβδος ΑΓ εφάπτεται στο σημείο Β με στερεό που αποτελείται από δύο ομοαξονικούς κυλίνδρους με ακτίνες R₁ = 0,1 m και R₂ = 0,2 m, όπως φαίνεται στο σχήμα . Η απόσταση του σημείου επαφής Β από το άκρο Γ της ράβδου είναι ℓ/4. Το στερεό μπορεί να περιστρέφεται χωρίς τριβές, σαν ένα σώμα γύρω από σταθερό οριζόντιο άξονα που περνάει από το κέντρο του. Ο άξονας περιστροφής συμπίπτει με τον άξονα συμμετρίας των δύο κυλίνδρων. Η ροπή αδράνειας του στερεού ως προς τον άξονα περιστροφής είναι Ι = 0,09 kgm². Γύρω από τον κύλινδρο ακτίνας R₁ είναι τυλιγμένο αβαρές και μη εκτατό νήμα στο άκρο του οποίου κρέμεται σώμα μάζας m = 1 kg

α. Να υπολογίσετε την κατακόρυφη δύναμη που δέχεται η ράβδος στο σημείο Β από το στερεό μονάδες 6

η λύση

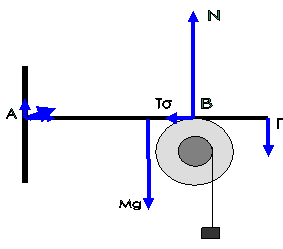
Θεωρούμε ΣΩΜΑ τη ράβδο. Το ΦΑΙΝΟΜΕΝΟ είναι ΙΣΟΡΡΟΠΙΑ. Εφαρμόζουμε τον πρώτο ΝΟΜΟ της κίνησης και για τον σκοπό αυτό σημειώνουμε τις ασκούμενες στο σώμα «ράβδος» δυνάμεις. Είναι η βάρος ίση με Μg = 30 N, μια δύναμη F_αρθ με άγνωστη κατεύθυνση που της ασκεί η άρθρωση στο σημείο Α, η κατακόρυφη δύναμη στο σημείο Γ , έστω F_Γ ίση με 9Ν, η ζητούμενη κατακόρυφη δύναμη – τη συμβολίζουμε με Ν στο σημείο Β και η στατική τριβή, έστω Τ_σ στο σημείο Β. Σύμφωνα με τον πρώτο ΝΟΜΟ της κίνησης, η συνισταμένη των ασκουμένων δυνάμεων είναι μηδέν. Από τις τρεις ανεξάρτητες εξισώσεις που το περιγράφουν επιλέγουμε την Στ_Α = 0

το αλγεβρικό άθροισμα των ροπών ως προς Α ίσο με μηδέν

Οι ροπές της Τ_σ και της F_αρθ ειναι μηδενικές

- Ν3L/4 + F_ΓL + ΜgL/2 = 0 και τελικώς Ν = 32Ν

β. Αν το σώμα μάζας m ισορροπεί, να βρείτε το μέτρο της δύναμης της στατικής τριβής μεταξύ της ράβδου και του στερεού μονάδες 6

η λύση

θεωρούμε το σύστημα «στερεό Σ με τους δύο κυλίνδρους- νήμα – σώμα m» . Το ΦΑΙΝΟΜΕΝΟ είναι ΙΣΟΡΡΟΠΙΑ. Εφαρμόζουμε τον πρώτο ΝΟΜΟ της κίνησης και για τον σκοπό αυτό σημειώνουμε τις ασκούμενες στο σύστημα δυνάμεις. Αυτές είναι

η W_Σ, βάρος του στερεού Σ,

η Ν΄, αντίδραση της Ν – σύμφωνα με τον τρίτο νόμο της κίνησης μια δύναμη μέτρου Ν –

η Τ_σ΄ αντίδραση της ζητούμενης στατικής τριβής – σύμφωνα με τον τρίτο νόμο της κίνησης μια δύναμη μέτρου Τ_σ –

η βάρος mg του σώματος και μια δύναμη, F_αξ , ασκούμενη από τον άξονα περιστροφής.

Σύμφωνα με τον πρώτο ΝΟΜΟ της κίνησης, η συνισταμένη των ασκουμένων δυνάμεων είναι μηδέν. Από τις τρεις ανεξάρτητες εξισώσεις που το περιγράφουν επιλέγουμε την Στ_cm = 0

το αλγεβρικό άθροισμα των ροπών ως προς το κέντρο μάζας του στερεού ίσο με μηδέν

Εφόσον οι ροπές των Ν’, W_Σ, F_αξ είναι μηδενικές

mgR₁– Τ_σ΄R₂= 0 και τελικώς Τ_σ ΄ = 5Ν

οπότε - σύμφωνα με τον τρίτο νόμο της κίνησης - θα είναι και Τ_σ = 5Ν

γ. Στο σημείο επαφής Β μεταξύ ράβδου και στερεού ρίχνουμε ελάχιστη ποσότητα λιπαντικής ουσίας έτσι ώστε να μηδενιστεί η τριβή χωρίς να επιφέρει μεταβολή στη ροπή αδράνειας του στερεού. Να υπολογίσετε την ταχύτητα του σώματος τη στιγμή που έχει ξετυλιχθεί νήμα μήκους 0,5 m.

η λύση

θεωρούμε το σύστημα «στερεό Σ με τους δύο κυλίνδρους- νήμα – σώμα m».

Το ΦΑΙΝΟΜΕΝΟ είναι η χωρίς ενεργειακές απώλειες κίνηση, Το σώμα μάζας m – θεωρούμενο υλικό σημείο θα εκτελεί ευθύγραμμη κίνηση σε κατακόρυφη τροχιά και το στερεό Σ θα εκτελεί στροφική κίνηση. Εφαρμόζουμε τον ΝΟΜΟ « ΔΙΑΤΗΡΗΣΗ ΤΗΣ ΕΝΕΡΓΕΙΑΣ». Θεωρούμε οριζόντια επιφάνεια αναφοράς για τη δυναμική ενέργεια ένα επίπεδο που διέρχεται από τη θέση που θα βρεθεί το σώμα μάζας m τη στιγμή που το νήμα θα έχει ξετυλιχθεί κατά 0,5 m

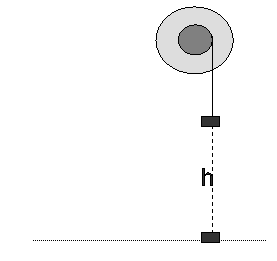
Κατά τη στιγμή εκείνη η ΚΙΝΗΤΙΚΗ ΕΝΕΡΓΕΙΑ του συστήματος θα είναι ½mυ² + ½Ιω²

Όπου ω η γωνιακή ταχύτητα της περιστροφής του Σ η οποία σχετίζεται με την ταχύτητα υ_Λ του σημείου που ξεκινάει το νήμα με την υ_Λ = ωR₁ . Αλλά η υ_Λ είναι σε κάθε στιγμή ίση με την ταχύτητα υ

του κατακόρυφα κινουμένου σώματος

του σημείου με την

W_Σ Η + mgh = W_Σ Η +½mυ² + ½Ιω²

υ = ωR₁ ω = υ/R₁ .

mgh = ½mυ² + ½Ιυ²/R₁² και τελικά υ = 1 m/s

μονάδες 6

Η λύση θα μπορούσε να βασιστεί και σε εφαρμογή του δεύτερου ΝΟΜΟΥ της κίνησης

α. στο ΦΑΙΝΟΜΕΝΟ « στροφική κίνηση του Σ» τ = Ια_γων

β. στο ΦΑΙΝΟΜΕΝΟ «ευθύγραμμη κίνηση του σώματος μαζας m» F = m a

δ. Να υπολογίστε τον ρυθμό παραγωγής έργου στο στερεό τη χρονική στιγμή που έχει ξετυλιχθεί νήμα μήκους 0,5 m. Δίνεται g = 10 m/ s². μονάδες 6

η λύση

Το ζητούμενο είναι ο ρυθμός μεταβίβασης ενέργειας στο στερεό Σ.

Η μεταβίβαση ( μεταφορά ) ενέργειας γίνεται με τη δράση της δύναμης F_N την οποία ασκεί το

τεντωμένο νήμα σε σημείο ταχύτητας υ_Λ που απέχει R₁ από τον άξονα περιστροφής.

Είναι με άλλα λόγια η ΙΣΧΥΣ της δύναμης αυτής, ίση με το γινόμενο F_N υ_Λ .

για να την υπολογίσουμε χρειαζόμαστε τα F_N και υ_Λ .

Η ταχύτητα του σημείου Λ είναι σε κάθε στιγμή ίση με την ταχύτητα του κατακόρυφα κινούμενου σώματος και κατά τη στιγμή εκείνη είναι ίση με υ = 1m/s.

Για να υπολογίσουμε την τιμή της

εφαρμόζουμε τον δεύτερο ΝΟΜΟ της κίνησης

α. στο ΦΑΙΝΟΜΕΝΟ « στροφική κίνηση του Σ» F_N R₁ = Ια_γων

β. στο ΦΑΙΝΟΜΕΝΟ «ευθύγραμμη κίνηση του σώματος μαζας m» mg – F_N = ma

και εφόσον η γωνιακή επιτάχυνση α_γων συνδέεται με την επιτάχυνση του σώματος μαζας m με τη σχέση α = α_γωνR₁

απορρέει ότι F_N = 9 Ν και η μεταβιβαζόμενη ισχύς είναι ίση με 9 J/s

Σχόλιο. Ένα ακόμα δύσβατο μονοπάτι για τη μεγάλη πλειοψηφία των εξεταζομένων. Βασική αδυναμία του επιλεγέντος ζητήματος η δυσκολία της περιγραφής του όλου συστήματος τον οποίο ελάχιστη σχέση έχει με πραγματικές καταστάσεις.

Για να φθάσει κάποιος στη λύση πρέπει

να επινοήσει έννοιες που δεν υπάρχουν ούτε στα δεδομένα ούτε στα ζητούμενα όπως η ΡΟΠΗ ΜΙΑΣ ΔΥΝΑΜΗΣ, η ΓΩΝΙΑΚΗ ΕΠΙΤΑΧΥΝΣΗ, η ΓΩΝΙΑΚΗ ΤΑΧΥΤΗΤΑ, η ΔΥΝΑΜΙΚΗ ΕΝΕΡΓΕΙΑ ,

η ΚΙΝΗΤΙΚΗ ΕΝΕΡΓΕΙΑ, η ΙΣΧΥΣ,

να μπορεί να επιλέγει ποιο θα είναι το εκάστοτε σύστημα στο οποίο θα εφαρμοζει τους νόμους και να έχει την ευχέρεια να αλλάζει σύστημα

να μπορεί να εφαρμόζει ΠΡΩΤΟ ΝΟΜΟ ΤΗΣ ΚΙΝΗΣΗΣ για την ισορροπία στερεού σώματος, ΔΕΥΤΕΡΟ ΝΟΜΟ ΤΗΣ ΚΙΝΗΣΗΣ για στρεφόμενο στερεό, ΔΕΥΤΕΡΟ ΝΟΜΟ ΤΗΣ ΚΙΝΗΣΗΣ για υλικό σημείο, ή ΔΙΑΤΗΡΗΣΗ ΤΗΣ ΕΝΕΡΓΕΙΑΣ , τη σχέση ΙΣΧΥΣ = ΔΥΝΑΜΗ ΕΠΙ ΤΑΧΥΤΗΤΑ - ή την P= τω - τη σχέση επιτρόχια επιτάχυνση = γωνιακή επιτάχυνση επί ακτίνα τη σχέση ταχύτητα = γωνική ταχύτητα επί ακτίνα.

Πάντως μολονότι δεν παραβιάζει το πνεύμα της νομοθεσίας η οποία επιβάλλει το 4^ο θέμα να είναι ΠΡΟΒΛΗΜΑ, το φετινό 4^ο συνιστά ένα δύσκολο πρόβλημα.

Πέμπτη 31 Μαίου 2006 ώρα 23.00.

Ένα εικοσιτετράωρο μετά επανερχόμαστε εντυπωσιασμένοι από τη δημοσίευση των λύσεων σε εφημερίδες από συνεργαζόμενους φροντιστές. Σε αθηναϊκή εφημερίδα μεγάλης κυκλοφορία για το 3^ο θέμα με την ελαστική κρούση ( 3β ) διαβάζουμε την προτεινόμενη λύση:

Ελαστική κρούση της m₁ με την αρχικά ακίνητη m₂ .

υ₁΄= (m₁ -m₂) υ ₁. /(m₁ +m₂) υ₂΄= 2m₁ υ ₁. /(m₁ +m₂)

Σύμφωνα με αυτούς που την προτείνουν, ο εξεταζόμενος δεν αξιολογείται για το

« εάν είναι σε θέση να εφαρμόζει τους δύο ΝΟΜΟΥΣ Διατήρησης κατά την εξέλιξη του φαινομένου»

αλλά για το

«εάν ΘΥΜΑΤΑΙ ΤΟΝ ΤΥΠΟ υ₁΄= (m₁ -m₂) υ ₁. /(m₁ +m₂) » .

Ένα απομεινάρι της δεκαετίας του 80 το οποίο εξακολουθεί να επιβιώνει . Λες και στο ΑΝΑΛΥΤΙΚΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ στους ΣΚΟΠΟΥΣ ΓΙΑ ΤΗ ΔΙΔΑΣΚΑΛΙΑ ΤΗΣ ΦΥΣΙΚΗΣ περιέχεται « ΣΚΟΠΟΣ ΤΗΣ ΔΙΔΑΣΚΑΛΙΑΣ ΕΙΝΑΙ ΤΟ ΝΑ ΘΥΜΑΤΑΙ ΟΤΙ υ₁΄= (m₁ -m₂) υ ₁. /(m₁ +m₂) »

Το θεωρούμε καταπληκτικό

Ανδρέας Ιωάννου Κασσέτας