Ανδρέας Ιωάννου Κασσέτας
Οι λύσεις
1.
Οι παγοδρόμοι και το κοντάρι.
α. Ενώ η
ορμή του συστήματος των δυο παγοδρόμων είναι μηδενική η στροφορμή του
συστήματος είναι κάτι σαν «ροπή ζεύγους».
Είναι ίση με 2100 Js
ως προς οποιοδήποτε σημείο του επιπέδου.
Ο νόμος τον οποίο πρέπει να εφαρμόσουμε είναι η
ΔΙΑΤΗΡΗΣΗ ΤΗΣ ΣΤΡΟΦΟΡΜΗΣ .
Η στροφορμή του συστήματος μετά τη στιγμή που οι
δύο παγοδρόμοι πιάνουν το κοντάρι θα είναι 2100 Js και – δεδομένου ότι το κοντάρι ασκεί στον
κάθε παγοδρόμο δύναμη κάθετα στη αρχική ταχύτητά του - καθένας από τους δύο παγοδρόμους θα κινείται
σε κυκλική τροχιά με ταχύτητα μέτρου 10 m/s και η στροφορμή θα
είναι συνεχώς 2100 Js
β. Όταν τραβώντας το κοντάρι πλησιάσουν σε
απόσταση ενός μέτρου η στροφορμή θα συνεχίσει να είναι 2100 Js δεδομένου ότι το πλησίασμα στο 1/3 της
απόστασης θα γίνει χωρίς εξωτερικές ροπές. Αυτό οδηγεί στο ότι η ταχύτητα
καθενός θα είναι 30 m/s
γ. Η κινητική ενέργεια του συστήματος πριν
τραβήξουν το κοντάρι ήταν 7000 J
και μετά το πλησίασμα θα είναι 63000 J. Αυξήθηκε δηλαδή κατά 54000 J ή 9πλασιάστηκε
Ο τρόπος με
τον οποίο παρουσιάζεται η έννοια στροφορμή
- στα σχολικά εγχειρίδια αλλά και στα φροντιστηριακά βοηθήματα - οδηγεί τη
σκέψη των περισσότερων μαθητών αλλά και αρκετών φοιτητών στην ιδέα ότι «για να
έχει στροφορμή ένα σώμα πρέπει να στρέφεται και εφόσον είναι υλικό σημείο να
εκτελεί κυκλική κίνηση» ή στην ισοδύναμη ιδέα ότι « εφόσον
κάτι κινείται ευθύγραμμα δεν έχει νόημα
να αναζητούμε τη στροφορμή του » .
Αυτό βέβαια δεν
ισχύει . Η – ως προς ένα γεωμετρικό
σημείο - στροφορμή κάθε κινουμένου υλικού σημείου ή κινουμένου σώματος ΣΕ ΚΑΠΟΙΑ ΧΡΟΝΙΚΗ ΣΤΙΓΜΗ είναι η ΡΟΠΗ ΤΗΣ
ΟΡΜΗΣ του είναι δηλαδή ένα διάνυσμα που αναφέρεται σε μια χρονική στιγμή
ανεξάρτητα από το πως ΘΑ κινείται την επόμενη χρονική στιγμή.
2. Αν κοπεί ο σπάγκος.
α.
Για να υπολογίσουμε τη ζητούμενη επιτάχυνση του Σ2 εφαρμόζουμε τον δεύτερο νόμο της
κίνησης στο σώμα Σ2. Θα
χρειαστούμε ωστόσο και τον νόμο του Hooke
Εφόσον το
φυσικό μήκος του ελατηρίου είναι 14 cm,
το μήκος του σπάγκου 12 cm
και η σταθερά του ελατηρίου 150 N/m, η δύναμη F την οποία ασκεί το ελατήριο στο μάζας m2 σώμα Σ2 –
σύμφωνα με τον νόμο του Hooke - είναι ίσο με το
γινόμενο 150 N/m . 2 cm = 3 N. Σύμφωνα με τον δεύτερο νόμο της κίνησης
η επιτάχυνση του μάζας m2 σώμα Σ2
θα είναι α = F/m2 = 150 m/s2
β.
Για να υπολογίσουμε την ταχύτητα του Σ2 όταν
το ελατήριο αποκτά το φυσικό του μήκος
εφαρμόζουμε τη Διατήρηση της ορμής και τη
Διατήρηση της ενέργειας στο σύστημα
«Σ1 σπάγκος
ελατήριο Σ2 »
Αν είναι υ1 και υ2 οι
αλγεβρικές τιμές των δύο ταχυτήτων που αποκτούν τα σώματα τη στιγμή που το ελατήριο
αποκτά το φυσικό του μήκος, σύμφωνα με
τη Διατήρηση της ορμής
0
= m1υ1
+ m2υ2
σύμφωνα με τη Διατήρηση της ενέργειας
½ k(ΔL)2 = ½m1υ12 +
½m2υ22 .
Το k
παριστάνει τη σταθερά του ελατηρίου 150 N/m και το ΔL τη
διαφορά που παρουσιάζει το μήκος του και
είναι ίσο με 2cm.
Οι δύο εξισώσεις συνιστούν σύστημα με δύο αγνώστους, τις αλγεβρικές τιμές των δύο ταχυτήτων. Εάν
το λύσουμε θα έχουμε |υ2| =1,5 m/s.
γ.
Το κέντρο μάζας του συστήματος των Σ1 και Σ2 αρχικά είναι
το γεωμετρικό σημείο Ο σε απόσταση 3 cm από τη Σ1
και 9 cm
από τη Σ2
και κατά την κίνηση των δύο
σφαιρών από τη στιγμή που κόβεται το νήμα μέχρι τη στιγμή που η Σ2
θα συγκρουστεί με τη Σ1 θα παραμείνει ακίνητο. Τη στιγμή που η Σ2
φθάνει στη θέση της Σ3 δηλαδή σε απόσταση 84 cm από
τη θέση Ο του κέντρου μάζας, η Σ1 θα απέχει από το Ο 28 cm (
28 = 84/3 ) κι αυτό διότι η μάζα της είναι 3πλάσια από εκείνη της Σ2.
Άρα οι δύο σφαίρες θα απέχουν 28 + 84 =
112 cm.
δ.
Κατά το ΦΑΙΝΟΜΕΝΟ «ΕΛΑΣΤΙΚΗ ΚΡΟΥΣΗ» των σφαιρών Σ2 και Σ3
εφαρμόζουμε τη Διατήρηση της ορμής και
τη Διατήρηση της ενέργειας του συστήματος . Αν συμβολίσουμε με υ2 , V2 και V3
τις
αλγεβρικές τιμές των ταχυτήτων των δύο σφαιρών πριν και μετά την κρούση
m2υ2
= m2V2 + m3V3
½m2υ22 = ½m2V 22 + ½m3V 32
Η λύση του συστήματος δίνει |V3 | = 25 cm/s
3. Η μπίλια
στη λεκάνη
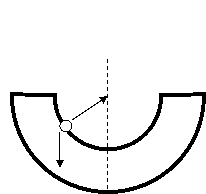
α. Εστιάζουμε στο κέντρο μάζας της μπίλιας.
Η κίνησή του είναι ίδια με εκείνη που ΘΑ έκανε ένα υλικό σημείο μάζας m στο οποίο θα δρούσαν οι ασκούμενες στη μπίλια δυνάμεις
Εφαρμόζουμε
τον δεύτερο νόμο της κίνησης για ένα υλικό σημείο το οποίο θα βρισκόταν στη
θέση του κέντρου μάζας το κέντρο μάζας ΤΗ ΣΤΙΓΜΗ που αφήνεται η μπίλια. Κατά τη
διεύθυνση της ακτίνας ισχύει
ΣF= maκ, Ν- mgσυν60 = maκ όπου aκ
η κεντρομόλος επιτάχυνση
του κέντρου μάζας. Κατά τη στιγμή
εκείνη εφόσον η ταχύτητα του κέντρου μάζας είναι μηδέν και η κεντρομόλος
επιτάχυνση είναι μηδέν.
Άρα Ν- mgσυν60 = 0 Ν = ½mg
β. Οι ασκούμενες στη μπίλια δυνάμεις σε μια
τυχαία στιγμή της κίνησης είναι το βάρος η κάθετη δύναμη N και η στατική τριβή Τ. Η κίνηση της μπίλιας θα είναι κύλιση
χωρίς ολίσθηση. Τη θεωρούμε σύνθεση μιας
μεταφορικής με την ταχύτητα και την επιτάχυνση του κέντρου μάζας και μιας
στροφικής περί άξονα που περνάει από το κέντρο μάζας.
Λόγω
της μεταφορικής κίνησης εφαρμόζουμε τον
δεύτερο νόμο της κίνησης για υλικό σημείο με την επιτάχυνση του κέντρου μάζας ΣFy= macm όπου αcm η ΕΠΙΤΡΟΧΙΑ επιτάχυνση του κέντρου
μάζας
mgημθ – Τ = m αcm
Εστιάζουμε
στη στροφικήκίνηση και εφαρμόζουμε τον δεύτερο νόμο
για στροφική κίνηση TR = Icmaγων
Το
Icm συμβολίζει τη ροπή αδράνειας του σφαιρικού σώματος ως προς τον
άξονα περιστροφής και το αγων τη γωνιακή
επιτάχυνση του στρεφόμενης σφαίρας περί τον ίδιο άξονα
Εφόσον
Icm = 2/5 m R2 και αcm = αγωνR
αcm
= 5/7 gημθ και T =2/7 mgημθ,
γ.
Εφαρμόζουμε τη Διατήρηση της
ενέργειας. Εξισώνουμε την ενέργεια της μπίλιας τη στιγμή που την αφήνουμε με
την ενέργεια της ίδιας μπίλιας τη στιγμή που έχει φθάσει στη βάση της λεκάνης .
Για τον υπολογισμό της δυναμικής ενέργειας θεωρούμε οριζόντια επιφάνεια
αναφοράς που να περνάει από το κέντρο μάζας τη στιγμή που βρίσκεται στη βάση
Έστω ότι κατά τη στιγμή που φθάνει στη βάση της λεκάνης η ταχύτητα του
κέντρου μάζας είναι υ.
mg5R( 1 – συν60 ) = 0 + ½mυ2 + ½ Icm ω2 .
Εφόσον Icm = 2/5 m R2 και υ = ωR
υ2 = 25gR/7.
δ.
Θεωρούμε το κέντρο μάζας εφαρμόζουμε τον δεύτερο νόμο της
κίνησης για την κίνησή του κατά τη στιγμή που η μπίλια περνάει από τη βάση της
λεκάνης.
Η κίνηση του κέντρου
μάζας είναι κυκλική με ακτίνα 5R
Ν
– mg = maκ
αλλά aκ = υ2/ 5R άρα
Ν – m g = mυ2/5R και εφόσον υπολογίσαμε ήδη ότι υ2
= 25gR/7
καταλήγουμε στο Ν
= 12mg/7.
δ.
Από τη σχέση T =2/7 mgημθ
συμπεραίνεται ότι καθώς κατεβαίνει η μπίλια η στατική τριβή
ελαττώνεται και ότι κατά τη στιγμή που θα βρεθεί στην κατώτερη θέση η στατική
τριβή μηδενίζεται
ε. Για να μη συμβαίνει
ολίσθηση πρέπει σε όλες τις θέσεις η τιμή της στατική τριβής να είναι μικρότερη
ή ίση από το γινόμενο μ Ν , όπου μ ο συντελεστής στατικής τριβής. Σε μια τυχαία
στιγμή της κίνησης κατά την οποία η ταχύτητα του κέντρου μάζας είναι υ1
εάν εφαρμόσουμε τον δεύτερο νόμο για την
κίνηση του κέντρου μάζας θα έχουμε – εκτός από τα παραπάνω – και ότι
N – mgσυνθ
= maκ
αλλά aκ = υ12/ 5R
όπου η ταχύτητα του
κέντρου μάζας κατά τη στιγμή εκείνη.
Η τιμή της υ1 μπορεί
να υπολογιστεί εάν εφαρμόσουμε τη Διατήρηση της ενέργειας με το να εξισώσουμε
την ενέργεια της μπίλιας τη στιγμή που αφήνεται με την ενέργεια την τυχαία
στιγμή της κίνησης
mg5R( 1 – συν60 ) = mg5R( 1
– συνθ ) + ½mυ2 + ½ Icm ω12 .
Εφόσον Icm = 2/5 m R2 και υ1 = ω1R
υ1
2 = 50gR(συνθ – ½ )
Από τα παραπάνω
προκύπτει ότι N
= mg/7(
17συνθ – 5 )
Για την τιμή της
στατικής τριβής αποδείχθηκε ότι T = 2/7
mgημθ
Για να μη γίνεται
ολίσθηση πρέπει Τ < μ Ν οπότε
τελικά μ > 2Ö3/7
4. Η πιο μεγάλη συσπείρωση
Η επιλογή των δύο νόμων διατήρησης και η εφαρμογή
τους
Κατά
την εξέλιξη του φαινομένου διατηρείται η ορμή, η στροφορμή και η ενέργεια του
συστήματος.
Επιλέγουμε τη Διατήρηση της ορμής και τη Διατήρηση
της ενέργειας και τις εφαρμόζουμε στο σύστημα των δύο σωμάτων
Για
τον σκοπό μας αυτό επιλέγουμε
δύο χρονικές στιγμές
από την εξέλιξη του φαινομένου
και εξισώνουμε τις αλγεβρικές
τιμές της ορμής που έχει το σύστημα κατά τις στιγμές εκείνες. Κάνουμε το ίδιο
και για τις τιμές της ενέργειας. Συμβολίζουμε με x τη μεταβολή στο μήκος του ελατηρίου, με m τη μάζα κάθε σώματος και με υ, V1,
V2 τις αλγεβρικές τιμές των ταχυτήτων των δύο
σωμάτων πριν και μετά τη συνάντηση του Α με το ελατήριο
σύμφωνα
με τη Διατήρηση της ορμής
mυ = mV1 + mV2
άρα υ = V1 + V2
σύμφωνα
με τη Διατήρηση της ενέργειας
½mυ12 = ½ kx2 + ½mV12 + ½mV22 άρα
υ2 = kx2/m + V12 + V22
Οι
αλγεβρικοί χειρισμοί
Το
ζητούμενο καθοδηγεί τους αλγεβρικούς μας χειρισμούς. Εφόσον ζητείται το μέγιστο
της συσπείρωσης η αλγεβρική μας στρατηγική είναι να δημιουργήσουμε τριώνυμο η
διακρίνουσα του οποίου θα οφείλει να είναι μη αρνητική
Από
τις δύο εξισώσεις προκύπτει
υ2 = kx2/m + V12
+ (υ -V1 ) 2
υ2 = kx2/m + V12
+ υ2 + V1 2 - 2 υV1 .
Κάνουμε
τις πράξεις και διατάσσουμε ως προς V1 V12- υV1 + kx2/2m = 0
Για
να έχει πραγματικές λύσεις ως προς V1
πρέπει η διακρίνουσα να είναι μεγαλύτερη η ίση από το μηδέν υ2- 4 kx2/2m >/ 0 άρα
xmax 2 = mυ2/2k
Από τη λύση της
δευτεροβάθμιας εξίσωσης προκύπτει ότι κατά τη στιγμή εκείνη η τιμή της V1 είναι ίση με το μισό
της υ. Άρα και η τιμή της V2
είναι ίση με το μισό της υ.
Η κινητική ενέργεια του
αρχικά κινούμενου σώματος έχει μοιραστεί εκείνη τη στιγμή η μισή στο ελατήριο
και η άλλη μισή στα δύο κινούμενα σώματα εξίσου.
Σκέψεις
ενός φυσικού
Κατά τη στιγμή που η
συμπίεση του ελατηρίου είναι μέγιστη ένας παρατηρητής κινούμενος με την
ταχύτητα του σώματος Β - ή «ξαπλωμένος» πάνω στο σώμα Β - διαπιστώνει ότι
το Α έχει πλησιάσει στη μικρότερη απόσταση και η σχετική του ταχύτητα ως προς
εκείνον είναι μηδενική. Στη συνέχεια στο σώμα Α απομακρύνεται από αυτόν τον
παρατηρητή απομακρύνεται δηλαδή από το Β, το μήκος συνεπώς του ελατηρίου
αυξάνεται. Σε κάποια χρονική στιγμή το ελατήριο επανακτά
το αρχικό του μήκος η δυναμική ενέργεια του ελατηρίου μηδενίζεται, το σώμα Α έχει ταχύτητα μηδέν και όλη η κινητική
ενέργεια του συστήματος είναι «κινητική ενέργεια του Β».
Το Α έχει μεταβιβάσει στο Β όλη του την ενέργεια.
Αποδειχτηκε ότι υ = V1 + V2 . Σε όλη δηλαδή την εξέλιξη
του φαινομένου το άθροισμα των ταχυτήτων
των δύο σωμάτων είναι σταθερό.
Η ταχύτητα του Α συνεχώς ελαττώνεται
( ασκείται δύναμη από το
συμπιεσμένο ελατήριο ΔΎΝΑΜΗ αντιτιθέμενη στην ταχύτητά του)
.
Η ταχύτητα
του Β συνεχώς αυξάνεται
( ασκείται από το συμπιεσμένο ελατήριο ΔΎΝΑΜΗ στην
ίδια κατεύθυνση με την ταχύτητά του ) .
Το κέντρο μάζας του
συστήματος κινείται
συνεχώς με αναλλοίωτη ταχύτητα υ/2 . Αυτό μπορεί να το αποδείξει κανείς εάν
σκεφτεί ότι η σταθερή ορμή του συστήματος είναι m υ και ότι
η ορμή κάθε συστήματος είναι ίση με το
γινόμενο της ολικής μάζας επί την ταχύτητα του κέντρου μάζας
mυ = 2mυcm υcm = ½υ
5. Με μεγάλη ταχύτητα ανατρέπεται.
Το σχήμα
Επιλέγουμε ένα σχήμα που
να παριστάνει την τομή του συστήματος με ένα κατακόρυφο επίπεδο το οποίο περνάει
από το κέντρο μάζας του κύβου
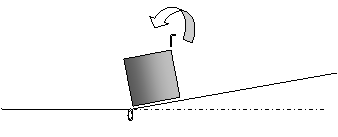
η ΦΥΣΙΚΗ είναι : ΑΝΤΙΚΕΙΜΕΝΑ, ΦΑΙΝΟΜΕΝΑ,
ΕΝΝΟΙΕΣ, ΝΟΜΟΙ
Τα
φαινόμενα
Η
μεταφορική κίνηση του κύβου στο κεκλιμένο
επίπεδο.
Το «κτύπημα». Όταν ο κύβος φθάσει
στη βάση, στο σημείο Ο, θα κτυπήσει στο οριζόντιο έδαφος. Με το κτύπημα
συμβαίνει αλλαγή κίνησης. Μέχρι τότε μεταφορική κίνηση, μετά το κτύπημα
στροφική περί Ο. Κατά το κτύπημα ( σύγκρουση ) ασκείται δύναμη στην ακμή Ο και μεταβάλλεται η ορμή του κύβου.
Διατηρείται όμως η στροφορμή του ως
προς Ο διότι ασκείται μεν η δύναμη αλλά δεν έχει ροπή ως προς Ο
Η στροφική κίνηση του
κύβου περί Ο. Κατά την εξέλιξή της
διατηρείται η ενέργεια του κύβου το άθροισμα δηλαδή κινητικής και (βαρυτικής)
δυναμικής ενέργειας
Η ανατροπή.
Θα συμβεί εφόσον με το κτύπημα το κέντρο βάρους του κύβου
ανέβει σε θέση τέτοια ώστε η προβολή του να βρεθεί αριστερά από τη γραμμική
βάση στήριξης που είναι στο σημείο Ο και η ροπή της δύναμης βάρος να είναι ροπή ανατροπής. Εάν δεν
συμβεί αυτό, το κέντρο βάρους θα φθάσει σε ένα υψηλότερο σημείο και ο κύβος θα «επιστρέψει»
Οι
νόμοι
Εφαρμόζουμε τη διατήρηση της ενέργειας για τον κύβο
κατά τη στροφική κίνηση περί Ο
Επιλέγουμε
δύο χρονικές στιγμές και εξισώνουμε τις τιμές της ενέργειας του σώματος.
Η μία είναι η στιγμή αμέσως μετά τη
«σύγκρουση» που έχει αρχίσει να εκτελεί στροφική κίνηση με «αρχική» γωνιακή
ταχύτητα ω0 ενώ το κέντρο μάζας του βρίσκεται σε ύψος h1 από το έδαφος. Η άλλη είναι η χρονική στιγμή που η διαγώνιος
ΟΓ γίνεται κατακόρυφη έτσι που το κέντρο μάζας να
βρίσκεται σε ύψος h2
από το οριζόντιο έδαφος,
και ο κύβος να έχει τη στιγμή εκείνη
γωνιακή ταχύτητα ω .
mg h1 + ½ Iοω02 = mgh2 + ½I0ω2
Γίνεται
φανερό ότι η τιμή της ω διαμορφώνεται από την αντίστοιχη της ω0.
Μπορούμε να δεχθούμε ότι η ελάχιστη τιμή
ω0min της γωνιακής ταχύτητας για την οποία θα
γίνει ανατροπή είναι εκείνη που αντιστοιχεί σε μηδενική τιμή της ω
mg
h1
+ ½ Iο ω0min2
= mgh2
Η
Γεωμετρία μας βοηθάει να υπολογίσουμε ότι h1 = δ συν30 /2 h1 = δÖ3/4 και
h2= δ/2, όπου δ η διαγώνιος του τετραγώνου δ = αÖ2.
Το
βασιζόμενο στη Γεωμετρία θεώρημα των παραλλήλων αξόνων ( Steiner ) μας βοηθάει να υπολογίσουμε τη ροπή
αδράνειας του κύβου ως προς τον άξονα περιστροφής που περνά από το Ο. ΙΟ = Ιcm + mδ2/4 = 1/6 mα2 + ½ mα2
ΙΟ = 2/3 mα2.
Το ερώτημα. Η
εμπειρική προσέγγιση μας υπαγορεύει την εμπειρική ιδέα ότι η «αρχική» γωνιακή
ταχύτητα ω0 σχετίζεται με την ταχύτητα υ με την οποία ο κύβος φθάνει
στη βάση. Το ερώτημα όμως είναι « ποια είναι η σχέση ανάμεσα στην τιμή της υ
και στην τιμή της ω0;»
Η απάντηση
. Την απάντηση μας τη δίνει η θεωρητική ιδέα ότι
«με
το κτύπημα, η
ως προς Ο στροφορμή του σώματος διατηρείται».
Εφαρμόζουμε λοιπόν τη
Διατήρηση της στροφορμής.
Επιλέγουμε δύο χρονικές στιγμές και εξισώνουμε τις
τιμές της στροφορμής του σώματος.
Η
μία είναι η χρονική στιγμή αμέσως πριν από τη «σύγκρουση» κατά την οποία ο
κύβος εκτελεί μεταφορική κίνηση με ταχύτητα κέντρου μάζας ίση με υ, οπότε η ως
προς Ο στροφορμή του είναι mυα/2 .
Η άλλη χρονική στιγμή είναι η μετά το κτύπημα κατά την οποία ο κύβος έχει αρχίσει να
εκτελεί στροφική κίνηση περί Ο με γωνιακή ταχύτητα ω0 και η
στροφορμή του ως προς Ο είναι ίση με ΙΟω0.
mυminα/2 = ΙΟω0min.
Αν
συνδυάσουμε τη σχέση αυτή με την mg h1 + ½ Iοω0min2
= mgh2
και λάβουμε υπόψη ότι h1 = αÖ6/4 h2= αÖ2/2 Iο= 2/3
mα2
![]() καταλήγουμε στο ζητούμενο υmin = 0,713Öαg
καταλήγουμε στο ζητούμενο υmin = 0,713Öαg
6. Στεφάνι στην ανηφοριά
η ΦΥΣΙΚΗ είναι :
ΑΝΤΙΚΕΙΜΕΝΑ, ΦΑΙΝΟΜΕΝΑ, ΕΝΝΟΙΕΣ, ΝΟΜΟΙ
Τα αντικείμενα είναι βέβαια το στεφάνι ως πρωταγωνιστής, το
οριζόντιο έδαφος και το με επίπεδη επιφάνεια σώμα που το χαρακτηρίζουμε κεκλιμένο επίπεδο
Τα φαινόμενα και οι έννοιες
Η κύλιση του σώματος στο
οριζόντιο έδαφος. Μπορεί να
θεωρηθεί
είτε
ως σύνθετη κίνηση δηλαδή μεταφορική με την ταχύτητα του κέντρου μάζας +
στροφική περί άξονα που περνάει από το κέντρο μάζας
είτε
ως στροφική περί στιγμιαίο άξονα περιστροφής που περνάει από το εκάστοτε σημείο
επαφής
Το «κτύπημα» στο σημείο
Ο. Στο στεφάνι ασκείται
δύναμη από την επιφάνεια του κεκλιμένου επιπέδου στο σημείο Ο και συντελείται
αλλαγή της κίνησης. Η στήριξη του σώματος στο σημείο του εδάφους στο οποίο
μέχρι τότε ακουμπούσε παύει να υφίσταται. Εφόσον η ως προς Ο ροπή της δύναμης
είναι μηδενική, η ως προς Ο στροφορμή διατηρείται
Η
κύλιση στο κεκλιμένο επίπεδο. Μπορεί να θεωρηθεί
είτε
ως σύνθετη κίνηση δηλαδή «μεταφορική με την ταχύτητα του κέντρου μάζας +
στροφική περί άξονα που περνάει από το κέντρο μάζας ».
είτε
ως στροφική περί στιγμιαίο άξονα περιστροφής που περνάει από το εκάστοτε σημείο
επαφής
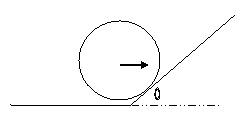
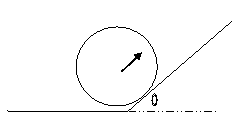
Άλλες έννοιες οι οποίες θα χρησιμοποιηθούν είναι η
γωνιακή ταχύτητα του στεφανιού λόγω της στροφικής κίνησης και η ροπή αδράνειας του
στεφανιού ως προς άξονα κάθετο στο επίπεδό του διερχόμενο από το κέντρο του .
Εφόσον το θεωρούμε ότι το στεφάνι είναι ένα
rigid body με όλα τα υλικά σημεία του σε σταθερή απόσταση
από τον άξονα η ροπή αδράνειας ως προς το κέντρο του είναι ίση με mR2.
Η
εφαρμογή του νόμου.
Εφαρμόζουμε
τη διατήρηση της στροφορμής ως προς το σημείο Ο.
Επιλέγουμε
δύο χρονικές στιγμές και εξισώνουμε τις
τιμές της στροφορμής του στεφανιού.
Η
μία χρονική στιγμή είναι πριν συγκρουστεί το στεφάνι με την επιφάνεια του
κεκλιμένου επιπέδου Η κίνηση του την θεωρούμε σύνθετη και η στροφορμή του
υπολογίζεται ως άθροισμα
της
στροφορμής ως προς Ο λόγω μεταφοράς η οποία είναι ίση με
mυ0d, όπου η απόσταση του Ο από τον φορέα της
ταχύτητας και
της
στροφορμής λόγω περιστροφής η οποία είναι ίση με το γινόμενο ροπή αδράνειας επί
γωνιακή ταχύτητα ω ίση με mR2ω0 – και
εφόσον ω0 =υ0/ R –
ίση τελικά με mυ0d .
Αξίζει
εδώ να σημειώσουμε πως όταν ένα σώμα όπως το στεφάνι εκτελεί μόνο στροφική
κίνηση η στροφορμή λόγω περιστροφής ως
προς ένα σημείου του άξονα περιστροφής είναι ίση με τη στροφορμή ως προς
οποιοδήποτε σημείο του επιπέδου. Το ίδιο ισχύει και για το άθροισμα των ροπών (
ολική ροπή ) δύο δυνάμεων που συνιστούν ζεύγος
Ως
δεύτερη χρονική στιγμή επιλέγουμε μία
στιγμή αμέσως μετά τη σύγκρουση. Το στεφάνι κυλίεται ανερχόμενο στο κεκλιμένο
επίπεδο και τη στιγμή εκείνη η ταχύτητα του κέντρου μάζας είναι υ. Η στροφορμή
του μπορεί να υπολογιστεί με ανάλογο τρόπο με τον προηγούμενο ως άθροισμα mυR + mυR = 2mυR
mυ0d + mυ0R = 2mυR . Βασιζόμενοι
στη Γεωμετρία μπορούμε να δείξουμε ότι d = Rσυν45
οπότε mυ0 Rσυν45
+ mυ0R = 2mυR άρα υ/υ0 = (1+ συν45 )/2 υ/υ0 = 0,853
7. Προς τα που ασκείται η δύναμη;
Για
να προσδιορίσουμε τις ασκούμενες στη ράβδο δυνάμεις - τη στιγμή που γίνεται οριζόντια -καταφεύγουμε στους νευτωνικούς νόμους της κίνησης
Εστιάζουμε
στο γεωμετρικό σημείο ΚΕΝΤΡΟ ΜΑΖΑΣ. Η κίνησή του συμπίπτει με την κίνηση που θα
έκανε ένα υποθετικό ΥΛΙΚΟ ΣΗΜΕΙΟ – με μάζα ίση μ ε τη μάζα του σώματος- στο
οποίο θα δρούσαν όλες οι ασκούμενες στο σώμα δυνάμεις.
ΕΠΙΤΑΧΥΝΣΗ
ΤΟΥ ΚΕΝΤΡΟΥ ΜΑΖΑΣ. Τη στιγμή που η
ράβδος είναι οριζόντια το κέντρο μάζας εκτελεί κυκλική κίνηση ακτίνας R = ½ L και έχει
κεντρομόλο επιτάχυνση για την οποία ισχύει ακ,cm
= υcm2/R
, όπου υcm η ταχύτητά του εκείνη τη χρονική στιγμή και R η ακτίνα της τροχιάς
για την οποί α ισχύει R = ½ L αλλά
και
επιτρόχια
επιτάχυνση η οποία
συνδέεται με τη γωνιακή επιτάχυνση με τη σχέση αε,cm
= αγων L/2
ΤΑΧΥΤΗΤΑ
ΤΟΥ ΚΕΝΤΡΟΥ ΜΑΖΑΣ. Σε κάθε χρονική στιγμή η
ταχύτητα υcm του κέντρου μάζας συνδέεται με τη γωνιακή ταχύτητα ω της ράβδου με τη σχέση υcm=ωL/2 οπότε για την κεντρομόλο
επιτάχυνση ισχύει και ακ,cm
= ω2L/2

![]() Σχέδιο με τις ασκούμενες
στη ράβδο δυνάμεις Σχέδιο με τις συνιστώσες της επιτάχυνσης του
κέντρου μάζας
Σχέδιο με τις ασκούμενες
στη ράβδο δυνάμεις Σχέδιο με τις συνιστώσες της επιτάχυνσης του
κέντρου μάζας
Η
επιτάχυνσή του κέντρου μάζας, σε κάθε χρονική
στιγμή, είναι ίση με την επιτάχυνση που
θα είχε ένα υποθετικό υλικό σημείο στο οποίο θα δρούσαν όλες οι ασκούμενες στο
σώμα δυνάμεις.
ΟΙ
ΑΣΚΟΥΜΕΝΕΣ ΔΥΝΑΜΕΙΣ. Οι ασκούμενες στη ράβδο δυνάμεις είναι το βάρος της mg
και η δύναμη που της ασκεί η άρθρωση, την οποία αναλύουμε σε δύο συνιστώσες, μία οριζόντια, την Fx , και μία κατακόρυφη
την Fy .
ΕΦΑΡΜΟΓΗ
ΤΟΥ ΝΟΜΟΥ . Θεωρώντας ένα υλικό σημείο με μάζα ίση με m το οποίο έχει κεντρομόλο και επιτρόχια επιτάχυνση, σύμφωνα με τον ΘΕΜΕΛΙΩΔΗ ΝΟΜΟ ΤΗΣ
ΜΗΧΑΝΙΚΗΣ (δεύτερο νόμο της
κίνησης) έχουμε
Fx
= mακ,cm Fx =
mω2L/2
mg - Fy
= mαε,cm
mg - Fy= mαγωνL/2
Για
να προσδιορίσουμε τις ζητούμενες δυνάμεις Fx και Fy χρειαζόμαστε
τη
γωνιακή επιτάχυνση και τη γωνιακή ταχύτητα της ράβδου τη στιγμή που είναι
οριζόντια
Για
να υπολογίσουμε τη γωνιακή επιτάχυνση της
ράβδου τη στιγμή που γίνεται οριζόντια καταφεύγουμε στο ΘΕΜΕΛΙΩΔΗ νευτωνικό ΝΟΜΟ
ΓΙΑ ΤΗ ΣΤΡΟΦΙΚΗ ΚΙΝΗΣΗ και τον εφαρμόζουμε στο σώμα ράβδος τη στιγμή που είναι οριζόντια.
Η
ολική ροπή ως προς Ο είναι ίση με το γινόμενο «ροπή αδράνειας επί γωνιακή
επιτάχυνση»
mgL/2 = 1/3mL2 αγων. αγων = 3g/2L
Για
να υπολογίσουμε τη γωνιακή ταχύτητα
της ράβδου τη στιγμή που γίνεται οριζόντια καταφεύγουμε στη ΔΙΑΤΗΡΗΣΗ ΤΗΣ
ΕΝΕΡΓΕΙΑΣ. Επιλέγουμε δύο κατάλληλες για τον σκοπό μας χρονικές στιγμές και
εξισώνουμε τις τιμές της ενέργειας της ράβδου mgL/2 + 0 = 0+ ½ Iω2 και εφόσον Ι = 1/3mL2 ,
mgL/2
= ½. 1/3mL2 ω2 άρα ω2= 3g/L
Fx = 3mg/2
Fy= mg/4
Από τις σχέσεις αυτές μπορούμε
να υπολογίσουμε το μέτρο
της δύναμης την οποία ασκεί στη ράβδο η άρθρωση και
να προσδιορίσουμε την
κατεύθυνσή της
8. Το ένα ευρώ και ο χάρακας
Υποθέτουμε
ότι μετά το κτύπημα το νόμισμα θα μείνει ακίνητο.
Η
κίνηση του χάρακα μετά το κτύπημα θα είναι σύνθεση μιας μεταφορικής με την
ταχύτητα Vcm του κέντρου μάζας και μιας στροφικής περί άξονα διερχόμενο
από το κέντρο μάζας
Για
το σύστημα νόμισμα- χάρακας:
1. Εφαρμόζουμε
τη ΔΙΑΤΗΡΗΣΗ ΤΗΣ ΟΡΜΗΣ.
Η ορμή οποιουδήποτε
συστήματος είναι ίση με το γινόμενο της μάζας επί την ταχύτητα του κέντρου
μάζας.
mυ = ΜVcm
2. Εφαρμόζουμε τη ΔΙΑΤΗΡΗΣΗ
ΤΗΣ ΣΤΡΟΦΟΡΜΗΣ ως προς το μέσον του χάρακα
mυd = Icmω
Η ως προς το κέντρο μάζας
στροφορμή λόγω της μεταφορικής κίνησης
είναι μηδέν
3. Εφαρμόζουμε τη
ΔΙΑΤΗΡΗΣΗ ΤΗΣ ΕΝΕΡΓΕΙΑΣ
½mυ2 = ½ MVcm2 + ½ Ιcmω2.
4. Άλγεβρα. Από τις τρεις αυτές
σχέσεις και εφόσον Ιcm
= ΜL2/12
, προκύπτει ότι ο λόγος των μαζών m/M είναι ίσος με L2/( L2+ 12d2) ανεξάρτητα από την
τιμή υ της ταχύτητας του νομίσματος. m/M = L2/( L2+ 12d2) m = ML2/(
L2+
12d2)
Συμπεραίνουμε ότι :
Ο δίσκος θα παραμείνει
ακίνητος εφόσον η μάζα του είναι ίση με ΜL2/( L2+ 12d2)
( Το β είναι σωστό )
Εάν - και μόνο εάν - το κτύπημα γίνει στο
μέσον του χάρακα, d=0, ο
δίσκος θα παραμείνει ακίνητος εφόσον m/M= L2/ L2 =1 ,
εφόσον δηλαδή η μάζα του νομίσματος είναι ίση με τη μάζα του χάρακα
( Τα α, γ και δ είναι λάθος )
9. Το τριγωνάκι για τα κάλαντα
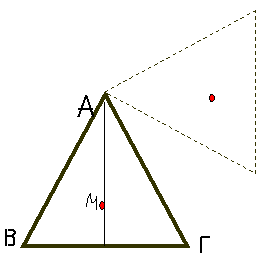
Α.
Σύμφωνα με τη Γεωμετρία :
Το
σημείο τομής των διαμέσων απέχει δ/3 από κάθε πλευρά
Για το μήκος δ κάθε
διαμέσου του ισοπλεύρου τριγώνου ισχύει δ2 = 3α 2/4
2. Σύμφωνα με το θεώρημα
Steiner
για τη ροπή αδράνειας κάθε πλευράς του τριγώνου ως προς άξονα κάθετο στο
επίπεδο του τριγώνου που περνάει από το σημείο Μ της τομής των διαμέσων ισχύει ΙΜ = 1/12 ma2 +
m
(δ/3)2 Ο συνδυασμός των παραπάνω οδηγεί στη σχέση ΙΜ = 1/6 ma2. Το ΙΜ παριστάνει τη ροπή αδράνειας
κάθε πλευράς ως προς τον άξονα Μ. Κατά συνέπεια η ροπή αδράνειας του τριγώνου
ως προς τον άξονα z
είναι ίση με ½ma2
. Ιz
=½ ma2
Β. Η κίνηση του τριγώνου είναι στροφική περί
άξονα οριζόντιο που περνάει από το καρφί Α. Εφαρμόζουμε τη Διατήρηση της
ενέργειας. Επιλέγουμε δύο κατάλληλες χρονικές στιγμές της κίνησης, την αρχική -
κατά την οποία η γωνιακή ταχύτητα είναι ω0min και η ΒΓ οριζόντια - και μία δεύτερη χρονική στιγμή κατά την
οποία η πλευρά ΒΓ να είναι κατακόρυφη και η γωνιακή
ταχύτητα μηδέν . Εξισώνουμε τις τιμές της ενέργειας του τριγωνικού σώματος
μάζας 3m.
Το κέντρο μάζας του
τριγωνικού σώματος είναι το σημείο
τομής των διαμέσων Μ.
Θεωρούμε οριζόντια
επιφάνεια αναφοράς για τη δυναμική ενέργεια διερχόμενη από τη θέση που
βρίσκεται το σημείο Μ πριν ενεργοποιήσουμε το τριγωνάκι. Όταν η ΒΓ γίνει οριζόντια το Μ θα έχει ανεβεί υψομετρικά κατά 2δ/3
= aÖ3/3.
½ ΙA ω0min2 + 0 = 0 + 3mg
aÖ3/3
Για την τιμή της ροπής
αδράνειας ΙΑ ως προς τον άξονα περιστροφής – σύμφωνα με το θεώρημα Steiner- ισχύει
ΙΑ = Ιz+3m(2δ/3)2 =
½ma2 + ma2
= 3/2 ma2 .
οπότε ½ 3/2 ma2ω0min2
= mgaÖ3/3 ω0min2 = 4Ö3g/9a
10. Η απερίγραπτη κίνηση της ράβδου.
Εφόσον
η δύναμη δεν ασκήθηκε στο κέντρο μάζας η κίνηση της ράβδου θα είναι σύνθετη.
Μεταφορική με την ταχύτητα του κέντρου μάζας και στροφική περί άξονα που
περνάει από το κέντρο μάζας
1.
η ΜΕΤΑΦΟΡΙΚΗ ΚΙΝΗΣΗ. Η ορμή κάθε σώματος ( ή συστήματος ) είναι ίση με το
γινόμενο της μάζας του επί την ταχύτητα του κέντρου μάζας. Εφόσον η ορμή που μεταβιβάστηκε στη ράβδο είναι 3 Ns και η μάζα της είναι 0,2 kg συνάγεται ότι το κέντρο μάζας θα αποκτήσει ταχύτητα 15 m /s στην
ίδια κατεύθυνση της δύναμης που ασκήθηκε. Η μεταφορική συνεπώς κίνηση θα
γίνεται με ταχύτητα 15 m /s
2.
η ΣΤΡΟΦΙΚΗ ΚΙΝΗΣΗ. Η ώθηση της δύναμης είναι ίση με τη μεταβιβαζόμενη ορμή.
Συνεπώς η ώθηση της ως προς το ΚΜ ροπής θα είναι ίση
με 3 Ns . 10cm = 0,3 Js και θα είναι κάθετη στο οριζόντιο επίπεδο που ανήκει το
διάνυσμα της μεταβιβαζόμενης ορμής. Η στροφορμή ως προς ΚΜ
την οποία θα αποκτήσει η ράβδος θα είναι συνεπώς 0,3 Js.
Αλλά
η ως προς ΚΜ στροφορμή είναι ίση με το γινόμενο της
ροπής αδράνειας της ράβδου ( 1/12 m L2 ) επί
τη γωνιακή ταχύτητα της περιστροφής περί τον κατακόρυφο άξονα 0,3 Js = 1/12 mL2. ω. Η τιμή της γωνιακής ταχύτητας θα είναι συνεπώς 200 rad /s.