Ανδρέας Ιωάννου Κασσέτας

Οι λύσεις των 11-20

11. Μετρώντας ενέργεια με ζυγό και με μεζούρα

η ΦΥΣΙΚΗ είναι : ΑΝΤΙΚΕΙΜΕΝΑ, ΦΑΙΝΟΜΕΝΑ, ΕΝΝΟΙΕΣ, ΝΟΜΟΙ

Τα αντικείμενα.

Ο στρεφόμενος δίσκος, το κομμάτι που αποσπάται

Τα φαινόμενα

Η στροφική κίνηση του δίσκου

Η απόσπαση του κομματιού από τον στρεφόμενο δίσκο.

Η κατακόρυφη κίνηση του κομματιού στο πεδίο βαρύτητας.

Οι έννοιες

Εκτός από τις έννοιες που εμπεριέχονται στα δεδομένα (μάζα δίσκου, ακτίνα δίσκου, μάζα κομματιού, ύψος) και στα ζητούμενα ( κινητική ενέργεια του δίσκου)

οι έννοιες τις οποίες πρέπει να «επιστρατεύσουμε» ώστε να οδηγηθούμε στη λύση είναι

η στροφορμή του δίσκου,

η ροπή αδράνειας του δίσκου,

η γωνιακή ταχύτητα του δίσκου

η ταχύτητα του κομματιού τη στιγμή που αποσπάται από τον δίσκο

η κινητική ενέργεια του κομματιού,

η βαρυτική δυναμική ενέργεια του κομματιού,

η επιτάχυνση της βαρύτητας

Οι νόμοι.

Κατά την εξέλιξή του ΦΑΙΝΟΜΈΝΟΥ «απόσπαση του κομματιού από τον στρεφόμενο δίσκο» διατηρείται η ΣΤΡΟΦΟΡΜΗ του συστήματος.

Κατά την εξέλιξή του ΦΑΙΝΟΜΈΝΟΥ «κατακόρυφη κίνηση του κομματιού» διατηρείται η ΕΝΈΡΓΕΙΑ του κομματιού. Η αντίσταση του αέρα θεωρείται αμελητέα.

Η εφαρμογή των νόμων

Κατά τη στροφική κίνηση του δίσκου η ζητούμενη κινητική ενέργεια είναι ίση ½Ιω², όπου Ι η ροπή αδράνειας του δίσκου και ω η γωνιακή ταχύτητα. Οι τιμές της – πριν και μετά την απόσπαση, τις οποίες συμβολίζουμε με Κ₁ και Κ₂ - είναι και τα ζητούμενα. Για να τις υπολογίσουμε χρειάζεται να προσδιορίσουμε τις τιμές - έστω ω₁ και ω₂ της γωνιακής ταχύτητας - διότι η ροπή αδράνειας θεωρείται γνωστή Ι₁ = ½ΜR² Ι₂ = ½ΜR² - mR²

Κ₁ = ½I₁ω₁² Κ₂ = ½I₂ω₂²

Κατά την απόσπαση του κομματιού εφαρμόζουμε τη ΔΙΑΤΗΡΗΣΗ ΤΗΣ ΣΤΡΟΦΟΡΜΗΣ στο σύστημα που ήταν ενιαίο και τώρα είναι δύο κομμάτια. Επιλέγουμε δύο χρονικές στιγμές και εξισώνουμε τις αλγεβρικές τιμές της στροφορμής του συστήματος

Ι₁ω₁ = Ι₂ω₂ + muR και εφόσον Ι₁ = Ι₂+ mR² και muR = mω₁R² θα είναι ω₁ = ω₂

Κατά την κατακόρυφη κίνηση του κομματιού εφαρμόζουμε τη ΔΙΑΤΗΡΗΣΗ ΤΗΣ ΕΝΕΡΓΕΙΑΣ στο κινούμενο κομμάτι. Επιλέγουμε δύο χρονικές στιγμές – η μία είναι η στιγμή που το κομμάτι έχει μόλις αποσπαστεί και εκτοξεύεται προς τα πάνω και η δεύτερη είναι η στιγμή που το κομμάτι έχει φθάσει σε ύψος Η και έχει στιγμιαία ταχύτητα μηδέν - και εξισώνουμε τις τιμές της ενέργειας

½ mυ ² + 0 = 0 + mgH άρα υ² = 2gH

Αλλά η τιμή της ταχύτητας υ σχετίζεται με την τιμή της γωνιακής ταχύτητας ω₁

υ = ω₁R συνεπώς ω₁² = 2gH/R² ,

Η ζητούμενη τιμή της κινητικής ενέργειας Κ₁ του δίσκου είναι

Κ₁ = ½. ½ΜR²ω₁² = ½.½MR²2gH/R² Κ₁ =½MgH

Η ζητούμενη τιμή της κινητικής ενέργειας Κ₂ του δίσκου είναι

Κ₂ = ½ Ι₂ω₂² Κ₂ =½(½MR²– mR²) 2gH/R²

Κ₂ = ½MgH - mgh .

12. Μπιλιάρδο. Το χτύπημα με τη στέκα

Στο σχήμα παριστάνεται μία κατακόρυφη τομή της μπίλιας από κατακόρυφο επίπεδο που περνάει από το κέντρο μάζας

Συμβολίζουμε με το γράμμα Σ το σημείο επαφής της μπίλιας με το τραπέζι.

Ας δούμε τι ακριβώς σημαίνει το γεγονός ότι « το χτύπημα έγινε από ψηλά».

Αν η μπίλια χτυπηθεί σε ύψος h =2R/5 από το κέντρο μάζας αποδεικνύεται βάσει των φυσικών νόμων ότι η στατική τριβή θα είναι μηδέν .

H δύναμη F θα είναι σε αυτή την περίπτωση συνισταμένη και

θα «ευθύνεται» εξ ολοκλήρου για τη διαμόρφωση της επιτάχυνσης του κέντρου μάζας α_0cm=F/m

η ώθησή της θα ευθύνεται εξ ολοκλήρου για τη μεταβίβαση στη μπίλια ορμής mu_0cm . mu₀ = Ω

η ώθηση της ροπής της ως προς το σημείο Σ θα ευθύνεται εξ ολοκλήρου για τη μεταβίβαση στη μπίλια στροφορμής – ως προς Σ - ίσης με Ω( h + R ) = I_Σω₀ = 7/5mR²ω₀.

( Ας μη μας διαφεύγει ότι η κίνηση χωρίς ολίσθηση είναι μια στροφική κίνηση περί στιγμιαίο άξονα περιστροφής διερχόμενο από το Σ . )

Εξάλλου για να ισχύουν οι σχέσεις Ω = mu₀ και Ω( h + R ) = 7/5mR²ω₀ με δεδομένο ότι υ_0cm = ω_0R πρέπει η τιμή του h να είναι ακριβώς ίση με 2R/5

Αν η μπίλια χτυπηθεί ψηλότερα από το h =2R/5 διαμορφώνεται στατική τριβή με την ίδια κατεύθυνση με την ασκούμενη δύναμη F, έτσι ώστε να ισχύουν οι νόμοι.

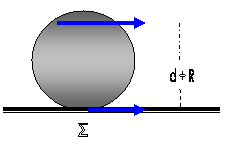
Έτσι εάν η ώθηση Ω της F στο ύψος 2R/5 προκαλεί μεταβίβαση ορμής mu₀ = Ω , ταχύτητα κέντρου μάζας u₀ και μεταβίβαση στροφορμής - ως προς Σ - Ω( ²/₅R + R ) = 7/5mR²ω₀ = 7/5mRu₀

μια ώθηση ίσου μέτρου σε σημείο ψηλότερα από το h = 2R/5 αντιστοιχεί σε μεγαλύτερη ώθηση ροπής - ως προς Σ - και έχει σαν αποτέλεσμα τη μεταβίβαση περισσότερης στροφορμής

Αν θέλουμε να προσδιορίσουμε το ύψος d στο οποίο πρέπει να γίνει το κτύπημα ώστε η ταχύτητα του κέντρου μάζας να είναι υ = 9υ₀/7

θα χρειαστεί να βασιστούμε στις σχέσεις Ω( d + R ) = ⁷/₅mR²ω = ⁷/₅mRu = ⁷/₅ mR9υ₀/₇

Ω( d + R ) = ⁹/₅ mRυ₀ και εφόσον Ω = mu₀ d = 4R/5

Αν η δύναμη ασκηθεί κάτω από τον οριζόντιο άξονα x που περνάει από το κέντρο μάζας για να της προσδώσουμε στη μπίλια μία ταχύτητα «προς τα πίσω» πρέπει η ασκούμενη αυτή δύναμη να αντιστοιχεί σε ώθηση ροπής τέτοια ώστε η στροφορμή -ως προς Σ- να έχει αντίθετη φορά

από εκείνη της προηγούμενης περίπτωσης. Στο σχήμα πρέπει η φορά της στροφορμής – άρα και της ώθησης της ροπής - να είναι προς τα έξω. Για να καταφέρουμε αυτό πρέπει η ασκούμενη δύναμη να έχει κατακόρυφη συνιστώσα προς τα κάτω

.

13. Ο σωλήνας μπορεί και να ανατραπεί;

Θεωρούμε ως ΣΩΜΑ τον κυλινδρικό σωλήνα. Θεωρούμε επίσης ότι βρίσκεται σε ισορροπία. Στο δρόμο που χάραξε ο Νewton ερμηνεύουμε την ισορροπία με τη βοήθεια της έννοιας ΔΥΝΑΜΗ Για τον σκοπό αυτό σημειώνουμε τις ασκούμενες στον σωλήνα δυνάμεις. Εκτός από την βάρος Mg και τις πιεστικές δυνάμεις F₁ και F₂ που ασκούνται – κάθετα στο τοίχωμα - από τις σφαίρες ασκείται και μια δύναμη από το έδαφος ο φορέας της οποίας περνάει από ένα σημείο Δ σε απόσταση x από το άκρο Α.

Εφόσον πρόκειται για ισορροπία η ολική ροπή σε κάθε σημείο του επιπέδου είναι ίση με μηδέν Με σκοπό να δημιουργήσουμε μια συνάρτηση του να περιγράφει τη σχέση του x με τα υπόλοιπα στοιχεία επιλέγουμε το σημείο Δ. F₁d –MgR – F₂r + Ν x = 0 όπου Ν η κατακόρυφη συνιστώσα της δύναμης από το έδαφος και d η υψομετρική απόσταση του κέντρου μάζας της αριστερά σφαίρας από το έδαφος. Λόγω της ισορροπίας ισχύει και

Ν = Mg οπότε F₁d –MgR – F₂r + Mgx = 0

Θεωρούμε στη συνέχεια ως ΣΩΜΑ το σύνολο των δύο σφαιρών το οποίο ισορροπεί. Οι ασκούμενες εξωτερικές δυνάμεις είναι οι πέντε του σχήματος. Δύο από αυτές αποτελούν αντιδράσεις των F₁ και F₂ οι οποίες αναφέρθηκαν πριν ως ασκούμενες στον κυλινδρικό σωλήνα. Έχουν συνεπώς μέτρο ίσο με το αντίστοιχο των F₁ και F₂

Εφόσον το σύστημα ισορροπεί η ολική ροπή ως προς οποιοδήποτε σημείο είναι ίση με μηδέν. Επιλέγουμε το σημείο Z την προβολή του κέντρου βάρους της δεξιά σφαίρας στο οριζόντιο έδαφος.

F₁d – mg( 2R -2r ) – F₂r = 0

Από τις σχέσεις αυτές προκύπτει ότι MgR -Mgx-2mg(R -r) = 0

x = R – 2(R- r)λ όπου λ = ο λόγος των μαζών m/M

Αν διαβάσουμε την τελευταία σχέση ως συνάρτηση x = f (λ) μας λέει ότι η αύξηση του λόγου λ θα συνεπάγεται ελάττωση της απόστασης x. Για μια ορισμένη μάλιστα τιμή του λόγου λ θα είναι x = 0.

Αυτό σημαίνει ότι η δύναμη που ασκεί το έδαφος θα δρα στο ακραίο σημείο Α και κάθε αύξηση του λόγου m/M θα οδηγήσει σε περιστροφή του συστήματος περί Α και στη συνέχεια σε ανατροπή.

Αυτό διότι η ροπή του ζεύγους των Ν και Mg το οποίο μέχρι τότε αντιστάθμιζε την υπόλοιπη ροπή δεν μπορεί να αυξηθεί περισσότερο δεδομένου ότι η δύναμη Ν δεν μπορεί να απομακρυνθεί άλλο από την δύναμη Mg.

0 = R – 2(R- r)λ λ = R /2(R-r) και με R=7r/4 θα είναι λ= m/M = 7/6

14. Η πιο μεγάλη γωνία

1. Ας αναζητήσουμε τη μέγιστη γωνία φ για την περίπτωση που στον τοίχο η τριβή είναι αμελητέα και στην επαφή ράβδου εδάφους ο συντελεστής στατικής τριβής είναι 0,5

Το φαινόμενο είναι η ΙΣΟΡΡΟΠΙΑ της ράβδου σε κατάσταση επικείμενης ολίσθησης

Για το ερευνήσουμε στο δρόμο που χάραξε ο Νεύτων καταφεύγουμε στην έννοια ΔΥΝΑΜΗ. θεωρούμε ως ΣΩΜΑ τη ράβδο, σημειώνουμε τις ασκούμενες στη ράβδο δυνάμεις. Είναι η δύναμη βάρος mg, η δύναμη Ν₁ που ασκεί ο τοίχος και η δύναμη που ασκεί το έδαφος

Μια λύση με βασικό εργαλείο την Άλγεβρα

Την δύναμη που ασκεί το έδαφος στη ράβδο μπορούμε να την «δούμε» σαν δύο δυνάμεις – κάθετη αντίδραση Ν₂ και στατική τριβή Τ₂ και εφόσον η ισορροπία της ράβδου είναι κατάσταση επικείμενης ολίσθησης η τιμή της στατικής τριβής θα είναι ίση με μN₂. Με αυτή την «οπτική» η ισορροπία ερμηνεύεται ως ανταγωνισμός δύο ζευγών Ν₂ και mg και από την άλλη Ν₁ και Τ₂ και ισότητα των ροπών τους

Κατά την ισορροπία της ράβδου ισχύουν τρεις ανεξάρτητες εξισώσεις

ΣFx = 0 Ν₁ = μΝ₂ .

ΣFy =0 Ν₂ = mg

Στ_Γ =0 Ν₁Lημφ – mg ½Lσυνφ = 0

εφφ = 1/2μ και με μ=0,5 εφφ=1 και φ =45⁰.

Μια λύση με περισσότερη Γεωμετρία

Την δύναμη που ασκεί το έδαφος στη ράβδο μπορούμε να την «δούμε» και σαν μία δύναμη F₂ η οποία σχηματίζει με την κατακόρυφο γωνία ω έτσι ώστε κατά την επικείμενη ολίσθηση εφω = μ.

Με αυτή την «οπτική» οι ασκούμενες δυνάμεις είναι τρεις και εφόσον ισορροπούν πρέπει οι φορείς τους να διέρχονται από το ίδιο σημείο Σ.

Η οπτική αυτή μας οδηγεί σε μια πιο ΓΕΩΜΕΤΡΙΚΗ λύση.

Στο τρίγωνο ΣΖΓ για τη γωνία ΖΣΓ – η οποία για λόγους «ευκλείδειους» είναι ίση με ω - ισχύει εφω = (ΖΓ)/(ΖΣ) αλλά ΖΓ = ½Lσυνφ και ΖΣ = Lημφ οπότε εφω = 1/2εφφ και - εφόσον εφω = μ -

θα είναι τελικά εφφ = 1/2μ

2. Ας αναζητήσουμε τη μέγιστη γωνία φ για την περίπτωση που και στα δύο σημεία στήριξης ο συντελεστής στατικής τριβής είναι 0,5

Το φαινόμενο το οποίο θεωρούμε είναι ΙΣΟΡΡΟΠΙΑ σε επικείμενη ολίσθηση. Θεωρούμε βέβαια ΣΩΜΑ τη ράβδο και σημειώνουμε τις ασκούμενες δυνάμεις. Ακολουθούμε τη γεωμετρική οδό και καθεμιά από τις ασκούμενες -στα σημεία στήριξης Α και Γ- δυνάμεις την βλέπουμε ως μία δύναμη η οποία σχηματίζει γωνία ω με την αντίστοιχη κάθετο. Οι ασκούμενες δυνάμεις είναι τρεις και για να ισορροπούν πρέπει να διέρχονται από το ίδιο σημείο Ρ.

Στο τρίγωνο ΖΡΓ ισχύει ( ΖΓ) = (ΖΡ) εφω. Για λόγους «ευκλείδειους»

(ΖΓ) = ½Lσυνφ (ΖΡ)= Lημφ+ ( ΕΡ) Αλλά ΕΡ=(ΑΕ)εφω

ΕΡ = ½Lσυνφεφω άρα ½Lσυνφ = [ Lημφ+½Lσυνφεφω ]εφω και εφόσον εφω = μ τελικά θα είναι εφφ= (1-μ² )/2μ

Αν αντικαταστήσουμε με μ = 0,5 θα είναι εφφ= ¾

15. Φρένο με δύο τριβές.

η ΦΥΣΙΚΗ είναι : ΑΝΤΙΚΕΙΜΕΝΑ, ΦΑΙΝΟΜΕΝΑ, ΕΝΝΟΙΕΣ, ΝΟΜΟΙ

Τα αντικείμενα. Ο κύλινδρος, ο τοίχος και το έδαφος

Το φαινόμενο. Η ΣΤΡΟΦΙΚΗ ΚΙΝΗΣΗ του κυλίνδρου για την οποία εύκολα αναγνωρίζουμε ότι είναι επιβραδυνόμενη.

Οι έννοιες . Εκτός από τα φυσικά μεγέθη που δίδονται ( γωνιακή ταχύτητα ω₀, ακτίνα του κυλίνδρου R , συντελεστής τριβής μ ) και το ζητούμενο χρονικό διάστημα t . Μπορούμε να διακρίνουμε ότι θα χρειαστούμε και την έννοια τριβή ολίσθησης, την έννοια ροπή, την έννοια γωνιακή ( επιβραδύνουσα ) επιτάχυνση α_γων, την έννοια μάζα και την έννοια ροπή αδράνειας.

Στο δρόμο που χάραξε ο Νεύτων σημειώνουμε τις δυνάμεις στον στρεφόμενο κύλινδρο σε μια τυχαία στιγμή της στροφικής του κίνησης, καθώς βρίσκεται σε συνεχή επαφή με τον τοίχο και το έδαφος. Οι δύο τριβές Τ₁ και Τ₂ σημειώνονται με κατεύθυνση αντίθετη της σχετικής ταχύτητα του σημείου επαφής ως προς τον τοίχο και το έδαφος αντίστοιχα.

Οι ΝΟΜΟΙ.

Για καθεμιά από τις τριβές ισχύει ο σχετικός νόμος σύμφωνα με τον οποίο

καθεμιά τους είναι ίση με το γινόμενο του συντελεστή επί την αντίστοιχη κάθετη αντίδραση

Τ₁ = μΝ₁ Τ₂ = μΝ₂ .

Για το φαινόμενο ΣΤΡΟΦΙΚΗ ΚΙΝΗΣΗ ισχύει ο θεμελιώδης νευτωνικός νόμος για τη στροφική κίνηση. Η ολική ροπή ως προς το κέντρο Ο είναι ίση με το γινόμενο ροπή αδράνειας ως προς τον άξονα περιστροφή επί γωνιακή επιτάχυνση. Από τις ασκούμενες δυνάμεις μόνο οι δύο τριβές έχουν ροπή ως προς Ο. μΝ₁R + μN₂R = ½ m R ² . α_γων

Από τη φορά της ολικής ροπής γίνεται φανερό ότι η επιτάχυνση α_γων περιγράφει - ως ρυθμός μεταβολής α_γων = dω/dt - την αδιάκοπη ελάττωση της γωνιακής του ταχύτητας

Για το φαινόμενο ΣΤΡΟΦΙΚΗ ΚΙΝΗΣΗ, εφόσον το κέντρο μάζας του σώματος παραμένει ακίνητο ισχύει ΣF_x = 0 Ν₁ = μΝ₂

ΣF_y = 0 Ν₂ + μΝ₁ – mg = 0

α_γων = 2μ(1+μ)g/ R(1+μ²)

Για το φαινόμενο ΣΤΡΟΦΙΚΗ ΚΙΝΗΣΗ με σταθερή επιβραδύνουσα γωνιακή επιτάχυνση από τη σκοπιά της κινηματικής περιγραφής του ισχύει

α_γων = dω/dt dω = α_γων dt - και εφόσον η α_γων είναι σταθερή - ω - ω₀ = α_γωνt

ω = ω₀ – α_γωνt

Αν εφαρμόσουμε τη σχέση αυτή για το χρονικό διάστημα t_ολ από τη στιγμή που γωνιακή ταχύτητα ήταν μηδέν μέχρι να σταματήσει

0 = ω₀ – α_γωνt_ολ . t_ολ = ω₀ /α_γων

και τελικά t_ολ = ω₀ R(1+μ²)/2μ(1+μ)g

16. Το βλήμα και η ξύλινη σφαίρα.

η ΦΥΣΙΚΗ είναι : ΑΝΤΙΚΕΙΜΕΝΑ, ΦΑΙΝΟΜΕΝΑ, ΕΝΝΟΙΕΣ, ΝΟΜΟΙ

Τα αντικείμενα.

Το βλήμα, η σφαίρα και το έδαφος

Τα φαινόμενα.

Η ευθύγραμμη κίνηση του βλήματος

Η συσσωμάτωση

Η κίνηση της σφαίρας με το ενσωματωμένο βλήμα

Οι έννοιες .

Είναι κατ’ αρχάς οι έννοιες που εμπεριέχονται στα δεδομένα ( μάζα βλήματος, ταχύτητα βλήματος, μάζα σφαίρας, ύψος στο οποίο γίνεται η πρόσκρουση, ακτίνα σφαίρας ). Το ζητούμενο «προσδιορισμός των βασικών στοιχείων της κίνησης» απαιτεί ως γνώση ότι το φαινόμενο «ΚΙΝΗΣΗ της σφαίρας» μπορεί να θεωρηθεί σύνθεση

μιας μεταφορικής περιγραφόμενης με την έννοια ΤΑΧΥΤΗΤΑ ΤΟΥ ΚΕΝΤΡΟΥ ΜΑΖΑΣ και μιας στροφικής περί άξονα που περνάει από το κέντρο μάζας περιγραφόμενης με την έννοια ΓΩΝΙΑΚΗ ΤΑΧΥΤΗΤΑ.

Εκτός από αυτές τις έννοιες θα χρειαστεί να επιστρατευτούν και άλλες έννοιες, όπως η ΟΡΜΗ, η ΣΤΡΟΦΟΡΜΗ, και η ΡΟΠΗ ΑΔΡΑΝΕΙΑΣ.

Οι νόμοι.

Το φαινόμενο « συσσωμάτωση» εφόσον δεν ασκούνται εξωτερικές δυνάμεις διατηρείται η ΟΡΜΗ του συστήματος καθώς και η ΣΤΡΟΦΟΡΜΗ του συστήματος ως προς το κέντρο μάζας.

Η εφαρμογή

Η εφαρμογή των αντίστοιχων νόμων οδηγεί στον ζητούμενο

1. Εφαρμόζουμε τη Διατήρηση της ορμής στο σύστημα

Εξισώνουμε την ορμή του συστήματος πριν τη συσσωμάτωση με την ορμή του συστήματος μετά τη συσσωμάτωση

mυ₀ = ΜV_cm

( η μάζα του βλήματος είναι αμελητέα πράγμα που σημαίνει ότι δεν επηρεάζει τη θέση του κέντρου μάζας και ότι το άθροισμα Μ + m μπορεί να θεωρηθεί ίσο με Μ )

Καταλήγουμε στο ότι το βασικό στοιχείο της μεταφορικής κίνησης,

η ταχύτητα V_cm του κέντρου μάζας, είναι V_cm= mυ₀ /Μ

2. Εφαρμόζουμε τη Διατήρηση της στροφορμής - ως προς το γεωμετρικό σημείο « κέντρο μάζας Κ » - στο σύστημα των δύο σωμάτων.

Εξισώνουμε την - ως προς Κ- στροφορμή του συστήματος πριν τη συσσωμάτωση με την - ως προς Κ- στροφορμή του συστήματος μετά τη συσσωμάτωση

Η σταθερή αυτή στροφορμή είναι ένα διάνυσμα κάθετο στο επίπεδο του σχήματος με φορά προς τα έξω

mυ₀½R= I_cmω

(η μάζα του βλήματος δεν επηρεάζει τη θέση του κέντρου μάζας και την τιμή της ροπής αδράνειας I_cm )

I_cm= ²/₅ΜR². mυ₀½R= ²/₅ ΜR²ω

Καταλήγουμε στο ότι το βασικό στοιχείο της στροφικής κίνησης η γωνιακή ταχύτητα του σώματος είναι ίση με ω= 5mυ₀/4MR

17. Το μισό καρπούζι

Το αντικείμενο (μισό καρπούζι) να θεωρηθεί ημισφαίριο μάζας m και ακτίνας R η ροπή αδράνειας του οποίου ως προς άξονα διερχόμενο από το διαμετρικό επίπεδο και από το κέντρο του κύκλου Ο είναι 2mR²/5. Το κέντρο μάζας του ημισφαιρίου βρίσκεται στον άξονα συμμετρίας σε απόσταση 3R/8 από το διαμετρικό επίπεδο.

Όταν το διαμετρικό επίπεδο γίνεται οριζόντιο η ακτίνα της τροχιάς του κέντρου μάζας να θεωρηθεί ίση με r.

Συμβολίζουμε με t τη χρονική στιγμή που το διαμετρικό επίπεδο γίνεται οριζόντιο. Συμβολίζουμε με το γράμμα Σ το σημείο στο οποίο το ημισφαιρικό σώμα αγγίζει το τραπέζι, κατά τη στιγμή t.

Μια βασική έννοια που πρωταγωνιστεί στην έρευνα είναι το κέντρο μάζας. Αρχικά βρίσκεται σε ύψος R από το οριζόντιο επίπεδο του τραπεζιού και τη στιγμή t βρίσκεται σε ύψος 5R/8.

Κατά την κίνηση του ημισφαιρικού σώματος η ΕΝΕΡΓΕΙΑ ΔΙΑΤΗΡΕΙΤΑΙ. Η κίνηση σύμφωνα και με τα δεδομένα μπορεί να θεωρηθεί στροφική περί στιγμιαίο άξονα που περνάει από το Σ. Συνεπώς, σύμφωνα με τη Διατήρηση της ενέργειας να έχουμε

mgR = mg5R/8 + ½I_Σω².

όπου ω η γωνιακή ταχύτητα κατά τη στιγμή t και Ι_Σ η ροπή αδράνειας ως προς τον στιγμιαίο άξονα περιστροφής

Σύμφωνα με το θεώρημα των παραλλήλων αξόνων ισχύει Ι_Σ = I_cm + m(5R/8)².

Σύμφωνα με το ίδιο θεώρημα ισχύει Ι₀ = Ι_cm + m(3R/8)². 2mR²/5 = Ι_cm + m(3R/8)².

Από τα παραπάνω προκύπτει ότι Ι_Σ = 13mR²/20

mgR = mg5R/8 + ½13mR²/20ω²

ω²= 15g/13R

Εφόσον το σώμα εκτελεί στροφική κίνηση με γωνιακή ταχύτητα ω, για την ταχύτητα του κέντρου μάζας – κατά τη στιγμή t – το οποίο συμμετέχει στη στροφική κίνηση σε απόσταση 5R/8 από τον στιγμιαίο άξονα περιστροφής ισχύει υ_cm²= ω².(5R/8)² .

υ_cm²= 25ω²R²/64 υ_cm²= 25.15gR/64.13 υ_cm² = 375gR/832

Θέτουμε τώρα στο οπτικό μας πεδίο την «περιπέτεια» του κέντρου μάζας στο σύνολό της . Εκτελεί μια καμπυλόγραμμη κίνηση και τη στιγμή t η ταχύτητά του είναι οριζόντια και η επιτάχυνσή του κεντρομόλος και ίση με υ²/r όπου r η ακτίνα καμπυλότητας. Η κίνησή του είναι ίδια με την κίνηση ενός υποθετικού υλικού σημείου - με μάζα ίση με τη μάζα m του σώματος- στο οποίο θα δρούσαν όλες οι ασκούμενες στο σώμα δυνάμεις. Ισχύει συνεπώς Ν – mg = mυ_cm²/r

Ν =mg + mgR375/832r

18. Η ανατροπή και η ανατροπή

Υποθέτουμε ότι ο κύλινδρος κινείται μεταφορικά χωρίς να ανατρέπεται και αναζητούμε την οριακή συνθήκη για να συμβαίνει αυτό

Τα ΦΑΙΝΟΜΕΝΑ είναι:

Η κίνηση του βαριδιού. Κίνηση υλικού σημείου

Η κίνηση του κυλίνδρου. Μεταφορική Κίνηση ενός rigid body

Η «ανατροπή» του κυλίνδρου

Για την επιταχυνόμενη κίνηση του βαριδιού εφαρμόζουμε τον δεύτερο νόμο της κίνησης σε μια τυχαία χρονική στιγμή

4mg – F_ν = 4ma

Για τη μεταφορική κίνηση του κυλίνδρου εφαρμόζουμε τον δεύτερο νόμο της κίνησης την ίδια χρονική στιγμή

F_ν = ma α = 4g/5 F_ν = 4mg/5

1. Η ανατροπή προς τα δεξιά.

Υποθέτουμε ότι η οριζόντια F_ν ασκείται «ψηλότερα από το κέντρο μάζας.

Φανταζόμαστε δύο αντίθετες δυνάμεις F₁ F₂ στο κέντρο μάζας καθεμιά με μέτρο F_ν= 4mg/5. Είναι μια τεχνική για να δούμε πιο καθαρά τη δράση των ασκουμένων δυνάμεων

Οι ασκούμενες δυνάμεις εμφανίζονται τώρα πέντε τον αριθμό και μπορούμε να θεωρήσουμε ότι έχουμε

τις τέσσερις σε δύο ζεύγη με αντίθετες ροπές και

την πέμπτη ασκούμενη στο κέντρο μάζας η οποία έχει ως αποτέλεσμα την κοινή επιτάχυνση α των υλικών σημείων του μεταφορικά κινουμένου σώματος

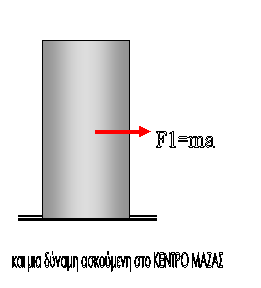
Τα δύο ζεύγη έχουν ίσες κατά μέτρο ροπές και εξασφαλίζεται η αρχική ισορροπία

F_ν ( h- H/2 ) = mgx όπου x η απόσταση x των mg και N και, εφόσον F_ν= 4mg/5, x = 4h/5 –4H/10

Αντικρίζουμε την τελευταία σχέση ως συνάρτηση x = 4h/5 – 4H/10

Αν αυξήσουμε το ύψος h στο οποίο ασκείται η δύναμη F_ν για να διατηρηθεί η ισορροπία των δύο ζευγών πρέπει να αυξηθεί η απόσταση x των mg και N. Αυτό όμως έχει ένα όριο δεδομένου ότι η δύναμη Ν ασκείται σε σημείο του κυλίνδρου, Το x έχει συνεπώς ως όριο το x_max = R/2.

Υπάρχει συνεπώς και ένα όριο στην τιμή του ύψους h R/2 = 4h_max/5- H/10

h_max= H/2 + 5R/8

2. Η ανατροπή προς τα αριστερά

Εάν η δύναμη του νήματος ασκηθεί «χαμηλά» μέσα από το ισοδύναμο διάγραμμα δυνάμεων μπορούμε να εξηγήσουμε γιατί είναι δυνατόν η ανατροπή του κυλίνδρου να γίνει προς την αντίθετη φορά από την προηγούμενη. Κατά τη μεταφορική κίνηση του κυλίνδρου ισχύει F_ν = ma α = 4g/5 F_ν = 4mg/5

Η ισορροπία των υπολοίπων δυνάμεων μας οδηγεί στις σχέσεις maH/2 –mah- mgx=0 όπου x η απόσταση x των mg και N και εφόσον α = 4g/5

m4g/5.H/2 –m4g/5h - mgx=0 x = 4H/10 – 4h/5

Αν δούμε τη σχέση αυτή ως συνάρτηση x = 4H/10 – 4h/5

Μπορούμε να διακρίνουμε ότι εάν ελαττώσουμε το το ύψος h στο οποίο ασκείται η δύναμη F_ν για να διατηρηθεί η ισορροπία των δύο ζευγών πρέπει να αυξηθεί η απόσταση x των mg και N. Αυτό όμως έχει ένα όριο.

Δεδομένου ότι η δύναμη Ν 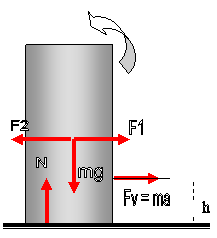ασκείται σε σημείο του κυλίνδρου, έχει ως όριο

το x_max = R/2. Υπάρχει συνεπώς και ένα ελάχιστο στην τιμή του ύψους h τέτοιο ώστε να ισχύει

R/2 = 4H/10 –4h_min/5 h_min = H/2 - 5R/8

( Το πρόβλημα μπορεί να λυθεί πιο εύκολα αν δούμε την κίνηση του κυλίνδρου ως επιταχυνόμενος παρατηρητής μεταφορικά κινούμενος με την επιτάχυνση α. Σε αυτή την θεώρηση χρειάζεται εκτός από τις ασκούμενες στον κύλινδρο «πραγματικές» δυνάμεις θα χρειαστεί να σημειώσει στο κέντρο μάζας του κυλίνδρου και την δύναμη αδρανείας με μέτρο ίσο με ma και 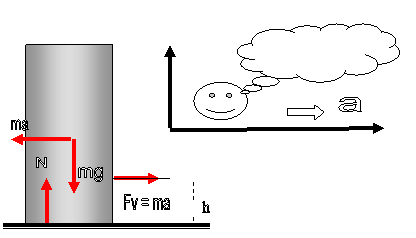κατεύθυνση αντίθετη της επιτάχυνσης α του συστήματος αναφοράς.

Το φαινόμενο το οποίο θα μελετήσει σε αυτή την περίπτωση θα είναι η ΙΣΟΡΡΟΠΙΑ του κυλίνδρου και η ενδεχόμενη ανατροπή του.

19. Μέτρηση του συντελεστή τριβής με υποδεκάμετρο.

Συμβολίζουμε με α το μήκος 16 cm της πλευράς της βάσης και με μ τον ζητούμενο συντελεστή στατικής τριβής

Ασκούμε οριζόντια δύναμη F σε «χαμηλό» ύψος y από το έδαφος έτσι ώστε να επιτυγχάνουμε ΙΣΟΡΡΟΠΙΑ και συγχρόνως ΕΠΙΚΕΙΜΕΝΗ ΟΛΙΣΘΗΣΗ του αντικειμένου

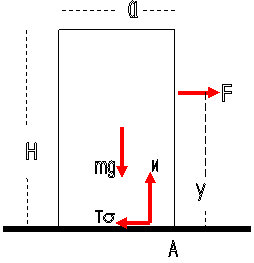
Οι σχέσεις ανάμεσα στις ασκούμενες δυνάμεις οι οποίες περιγράφουν την ΙΣΟΡΡΟΠΙΑ του είναι

F = T_σ Ν = mg Fy – mgx = 0 όπου x η απόσταση των φορέων των δυνάμεων βάρος και κάθετη αντίδραση

Η σχέση που περιγράφει την ΕΠΙΚΕΙΜΕΝΗ ΟΛΙΣΘΗΣΗ είναι η Τ_σ = μ Ν Προκύπτει ότι

x =μy

Αν δούμε τη σχέση αυτή ως συνάρτηση x =μy η ανάγνωσή της μας λέει ότι” κάθε απόπειρα ολίσθησης με σταθερή δύναμη σε ολοένα αυξανόμενο ύψος y θα συνεπάγεται την αύξηση του x της απόστασης δηλαδή της Ν από την mg» . Κατά την αύξηση όμως του x υπάρχει ένα μέγιστο που δεν είναι δυνατόν να παραβιαστεί. Είναι το x = ½a

Την ισορροπία μπορούμε να την περιγράψουμε και μέσα από τον «ανταγωνισμό»

του ζεύγους F – T το οποίο τείνει να περιστρέψει το αρχικά ακίνητο αντικείμενο κατά τη φορά των δεικτών του ρολογιού και η «ικανότητά του» περιγράφεται με τη ροπή του F. y

με το ζεύγος mg – N το οποίο τείνει να περιστρέψει το ίδιο αντικείμενο κατά την αντίθετη φορά και η «ικανότητά του» περιγράφεται με τη ροπή του mg. x . Tο φαινόμενο ΙΣΟΡΡΟΠΙΑ ερμηνεύεται με την ισότητα των μέτρων των δύο ροπών. F y = mg x. Εάν κάνουμε διάφορες δοκιμές αυξάνοντας το ύψος y, αυξάνουμε τη ροπή του ενός ζεύγους την Fy, οπότε για να μη συμβαίνει περιστροφή θα πρέπει να αυξάνεται και η ροπή του άλλου ζεύγους η mgx. Για την τιμή του x όμως υπάρχει ένα όριο το ½a το οποίο δεν μπορεί να ξεπεραστεί διότι η δύναμη Ν ασκείται οπωσδήποτε σε σημείο του σώματος. Αυτό σημαίνει ότι εάν το x γίνει η ροπή mgx δεν μπορεί να μεγαλώσει άλλο και θα συμβεί περιστροφή του σώματος περί το σημείο Α.

Σύμφωνα με τα δεδομένα του προβλήματος, η εμπειρία μας λέει ότι για y = h = 20 cm επίκειται η ανατροπή. Αυτό σημαίνει ότι για y = h έχουμε x = ½ a

Αν στη συνάρτηση y = μx βάλουμε y = h θα είναι x = ½ a. ½a = μh άρα

μ = a/2h μ = 0,25

20. Αν το βαρίδι είναι αρκετά βαρύ.

Συμβολίζω με α το μέτρο της επιτάχυνσης του βαριδιού και με m_β τη μάζα του .

1. Μελετώ την κίνηση του βαριδιού ως αδρανειακός παρατηρητής. Τη θεωρώ κίνηση υλικού σημείου για την οποία ισχύει ο δεύτερος νόμος της κίνησης. Σημειώνω τις δυνάμεις στο σώμα “βαρίδι” και m_βg - F_ν = m_βa

2. Μελετώ την κίνηση συστήματος «λεκάνη – σφαίρα» ως αδρανειακός παρατηρητής.

Τη θεωρώ μεταφορική κίνηση συστήματος το κέντρο μάζας του οποίου κινείται ευθύγραμμα με επιτάχυνση μέτρου α. Εφαρμόζω τον δεύτερο νόμος της κίνηση. Σημειώνω τις εξωτερικές δυνάμεις στο σύστημα «λεκάνη – σφαίρα» και F_ν = ( m + Μ ) a .

Από τις δύο μέχρι τώρα σχέσεις προκύπτει ότι α = m_βg/(m+M +m_β)

3. Μελετώ τη συμπεριφορά του σώματος «σφαίρα» ως μεταφορικά κινούμενος παρατηρητής επιταχυνόμενος με επιτάχυνση α, οπότε οι ασκούμενες στο σώμα δυνάμεις είναι :

οι δυνάμεις που θα σημείωνε ένας αδρανειακός παρατηρητής δηλαδή το βάρος mg και η δύναμη F₁ που ασκείται στη σφαίρα από τη λεκάνη

και η ασκούμενη στο κέντρο μάζας «ψευδοδύναμη» αδρανείας με μέτρο ίσο με το γινόμενο ma και κατεύθυνση αντίθετη της κατεύθυνση της επιτάχυνσης που έχει το δικό μου σύστημα αναφοράς.

Για μένα η σφαίρα ακινητεί άρα οι φορείς των τριών δυνάμεων πρέπει να διέρχονται από το ίδιο σημείο

Εφόσον οι δυνάμεις ισορροπούν η ολική ροπή των τριών δυνάμεων ως προς οποιοδήποτε σημείο είναι ίση με μηδέν. Επιλέγω το σημείο Α στο οποίο ασκείται η δύναμη F₁ . mad – mgx = 0, gx = ad.

όπου x η απόσταση του Α από την κατακόρυφο που περνά από το κέντρο μάζας ( φορά της δύναμης βάρος ) και d η απόσταση του Α από την οριζόντια που περνά από το κέντρο μάζας. Η σχέση gx = ad γράφεται και

α = gεφφ, όπου φ η γωνία της F₁ με την κατακόρυφο.

Αν δούμε την τελευταία αυτή σχέση ως συνάρτηση α = gεφφ διαπιστώνουμε ότι κάθε αύξηση της επιτάχυνσης α θα συνεπάγεται αύξηση της τιμής της γωνίας φ. Η μέγιστη γωνία φ_max που μπορεί να υπάρξει φ_max ώστε να διατηρείται η ισορροπία είναι η γωνία της ΓΚ με την κατακόρυφο (σχήμα ) οπότε για την αντίστοιχη επιτάχυνση α_max θα ισχύει α_max = gεφφ_max .

Η Γεωμετρία εξάλλου μας δείχνει ότι εφ²φ_max= R²– (R-h )² /( R-h )²

α_max = g ÖR²– (R-h )² /( R-h ). Αν συνδυάσουμε την τελευταία αυτή σχέση με την

α = m_βg/(m+M +m_β) μπορούμε να υπολογίσουμε τη ζητούμενη μάζα m_β ώστε η σφαίρα να διατηρείται μέσα στην κοιλότητα, άρα και τις τιμές της m_β ώστε να η σφαίρα να εξέλθει από την κοιλότητα